引言

上一节介绍了受限玻尔兹曼机叠加的逻辑，以及叠加过程中出现的$\text{Double Counting}$问题。本节将继续介绍，如何优化$\text{Double Counting}$问题，并对受限玻尔兹曼机叠加的整个思路进行总结。

回顾：受限玻尔兹曼机的叠加逻辑

在深度信念网络——模型构建思想中介绍了关于受限玻尔兹曼机叠加的底层逻辑——相比于单纯的受限玻尔兹曼机结构，虽然受限玻尔兹曼机因自身特殊的结构性质能够通过 极大似然估计 + 梯度上升 的方式对模型结构中的参数进行近似求解：

• 牛顿-莱布尼兹公式
• 在第$t$次迭代过程中，并没有对完整${\mathcal{W}}^{(t)}$进行梯度求解，而仅仅示例了样本$v^{(i)}$对应的某隐变量$h_k^{(i)}$与某观测变量$v_j^{(i)}$之间关联关系的参数${\mathcal{W}}_{j\iff k}^{(i)}$的梯度结果。
• 其中${\sum }_{v^{(i)}}\mathcal{P}(v^{(i)})\cdot \mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}$部分使用‘对比散度’加快采样和计算过程。
  $$\begin{array}{rl}{\mathcal{W}}^{(t+1)}& \Leftarrow {\mathcal{W}}^{(t)}+\eta {\nabla }_{{\mathcal{W}}^{(t)}}\mathcal{L}({\mathcal{W}}^{(t)})\\ {\nabla }_{{\mathcal{W}}^{(t)}}\mathcal{L}({\mathcal{W}}^{(t)})& ={\nabla }_{{\mathcal{W}}^{(t)}}\left[\sum _{i=1}^N\log \mathcal{P}(x^{(i)};{\mathcal{W}}^{(t)})\right]\\ & =\sum _{i=1}^N{\nabla }_{{\mathcal{W}}^{(t)}}\left[\log \mathcal{P}(x^{(i)};{\mathcal{W}}^{(t)})\right]\\ {\nabla }_{{\mathcal{W}}^{(t)}}\left[\log \mathcal{P}(x^{(i)};{\mathcal{W}}^{(t)})\right]& \Rightarrow \frac{\partial }{\partial {\mathcal{W}}_{j\iff k}^{(i)}}\left[\log \mathcal{P}(x^{(i)};{\mathcal{W}}^{(t)})\right]\\ & =\mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}-\sum _{v^{(i)}}\mathcal{P}(v^{(i)})\cdot \mathcal{P}(h_k^{(i)}=1\mid v^{(i)})\cdot v_j^{(i)}\end{array}$$

但这种方式仅能保证将梯度参数向最优参数方向收敛，在每次迭代过程内部可能并没有达到最优性能。也就是说，梯度更新过程中性能可以进一步提升。而 受限玻尔兹曼机叠加 思想为迭代过程中性能提升做了理论上的背书：

• 从变分推断的角度观察，可以将对数似然函数$\log \mathcal{P}(v)$表示成如下形式：
  • 其中$h^{(i)}$表示某具体样本$v^{(i)}$对应在模型中的隐变量集合;$\mathcal{Q}(h^{(i)}\mid v^{(i)})$表示人为引入的关于隐变量的后验概率分布。
  • 如果想要求解$\mathcal{Q}(h^{(i)}\mid v^{(i)})$也不麻烦，因为受限玻尔兹曼机的结构性质可以对条件概率分布直接求解。详见受限玻尔兹曼机——后验概率

$$\begin{array}{rl}\log \mathcal{P}(v)& =\sum _{i=1}^N\log \mathcal{P}(v^{(i)})\\ \log \mathcal{P}(v^{(i)})& =\log \sum _{h^{(i)}}\mathcal{Q}(h^{(i)}\mid v^{(i)})\cdot \frac{\mathcal{P}(h^{(i)},v^{(i)})}{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\\ & =\log {\mathbb{E}}_{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\left[\frac{\mathcal{P}(h^{(i)},v^{(i)})}{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\right]\end{array}$$

• 由于$\log$函数是凹函数，那么必然有：
  这里是通过杰森不等式的逻辑推导的，也可以通过变分推断$\text{ELBO + KLDivergence}$角度进行描述。
  $$\begin{array}{rl}\log \mathcal{P}(v^{(i)})& =\log {\mathbb{E}}_{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\left[\frac{\mathcal{P}(h^{(i)},v^{(i)})}{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\right]\\ & \ge {\mathbb{E}}_{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\left[\log \frac{\mathcal{P}(h^{(i)},v^{(i)})}{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\right]=\text{ELBO}\end{array}$$
  $\text{ELBO}$被称为证据下界($\text{Evidence of Lower Bound}$)，其本质就是对数似然函数的下界结果。如果能够使证据下界达到最大，当前迭代步骤的对数似然函数也能够被提升到极致。
• 但在正常的梯度上升过程中，可以通过 上一迭代步骤产生的模型参数计算出当前步骤的$\text{ELBO}$，但不能保证它是当前步骤的最大值，为了改进该问题，可以将上式继续展开：
  • 后项是常数的原因在于，基于样本条件下，完全可以通过当前样本计算$\mathcal{Q}(h^{(i)}\mid v^{(i)})$;
  • 在$\mathcal{Q}(h^{(i)}\mid v^{(i)})$计算结束之后，通过该分布可以采集大量关于隐变量后验样本，并基于该样本得到观测变量$\mathcal{P}(v^{(i)}\mid h^{(i)})$的后验结果(幻想粒子的生成过程)。
    $$\begin{array}{rl}\text{ELBO}& =\sum _{h^{(i)}}\mathcal{Q}(h^{(i)}\mid v^{(i)})\log \left[\mathcal{P}(h)\cdot \frac{\mathcal{P}(v^{(i)}\mid h^{(i)})}{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\right]\\ & =\sum _{h^{(i)}}\mathcal{Q}(h^{(i)}\mid v^{(i)})\log \mathcal{P}(h^{(i)})+\underset{常数}{\underbrace{\sum _{h^{(i)}}\mathcal{Q}(h^{(i)}\mid v^{(i)})\log \left[\frac{\mathcal{P}(v^{(i)}\mid h^{(i)})}{\mathcal{Q}(h^{(i)}\mid v^{(i)})}\right]}}\end{array}$$
• 如果是受限玻尔兹曼机，在当前迭代步骤中，确实可以通过当前迭代步骤的模型参数对$\mathcal{P}(h^{(i)})$进行求解：
  概率密度函数$\mathcal{P}(h^{(i)},v^{(i)})$完全可以通过模型参数进行精确表示。
  $$\mathcal{P}(h^{(i)})=\sum _{v^{(i)}}\mathcal{P}(h^{(i)},v^{(i)})$$
  但也仅限于能够求解，该结果是否优秀并不知晓；如果将受限玻尔兹曼机叠加，也就是说，使用另一组隐变量学习$h^{(i)}$;这里称之为$h^{(i;2)}$,$h^{(i;2)}$中的各隐变量节点与$h^{(i)}$中的各节点之间也存在关联关系。此时就出现另一个 由$h^{(i)},h^{(i;2)}$节点构成的新的受限玻尔兹曼机。
  该受限玻尔兹曼机在参数学习过程中通过极大似然估计给$\log \mathcal{P}(h^{(i)})$做理论背书：通过叠加产生的新$\text{RBM}$，其模型参数必然满足$\log \mathcal{P}(h^{(i)})$达到最大；从而使$\text{ELBO}$达到最大；最终使$\log \mathcal{P}(v^{(i)})$达到最大。

至此，受限玻尔兹曼机叠加可以提高模型的学习性能。

回顾：受限玻尔兹曼机叠加过程中的计算方式

如果仅仅是将两个受限玻尔兹曼机叠加成一个三层混合模型，那么需要观察隐变量集合$h^{(i)}$对于不同层的后验概率：
$$\mathcal{P}(h^{(i)})=\{\begin{array}{l}{\sum }_{h^{(i;2)}}\mathcal{P}(h^{(i)},h^{(i;2)};{\mathcal{W}}^{(i;2)})\\ {\sum }_{v^{(i)}}\mathcal{P}(h^{(i)},v^{(i)};{\mathcal{W}}^{(i)})\end{array}$$
这两个受限玻尔兹曼机都有各自的参数去表示$\mathcal{P}(h^{(i)})$。

• 普通的$\text{RBM}$自然是仅使用$\mathcal{P}(h^{(i)},v^{(i)})$中的模型参数${\mathcal{W}}^{(i)}$进行表示；
• 如果仅使用$\mathcal{P}(h^{(i)},h^{(i;2)})$中的模型参数${\mathcal{W}}^{(i;2)}$进行表示，那意味着$\mathcal{P}(h^{(i)})$只和$h^{(i)},h^{(i;2)}$组成的受限玻尔兹曼机有关。这需要 $h^{(i;2)}$和$v^{(i)}$之间没有关联关系，对应产生的模型结构就是深度信念网络结构。

但如果从客观角度观察，在混合模型中，无论是使用哪个受限玻尔兹曼机单独表示，都是不准确的。一种朴素想法在于：无论是$\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i)})$还是$\mathcal{P}(h^{(i;2)};{\mathcal{W}}^{(i;2)})$，都将其计算出来，并将其结果结合起来：
$$\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i)},{\mathcal{W}}^{i;2})=\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i)})+\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i;2)})$$

但这种直接结合的方式本身存在$\text{Double Counting}$问题，在计算$\mathcal{P}(h^{(i)})$时，样本集合${\left\{v^{(i)}\right\}}_{i=1}^N$在采样过程中，被重复使用两次；
这仅仅是原始$\text{RBM}$基础上多叠加了一层，叠加的层数越多，被重复利用的次数越多。
详见深度玻尔兹曼机——预训练过程

关于计算过程的优化

针对上述描述，可以知道：

• 受限玻尔兹曼机叠加产生的混合模型能够增加模型性能；
• 无论使用哪一个受限玻尔兹曼机描述$\mathcal{P}(h^{(i)})$，都不准确；但仅将不同模型对于$\mathcal{P}(h^{(i)})$的结果相加，会出现 $\text{Double Counting}$现象。因此需要对该操作进行优化。

常见的方式，可以将系数减半，也就是取算数平均值：
值得注意的是，这种操作并不仅仅是将$\mathcal{P}(h^{(i)},{\mathcal{W}}^{(i)})$与$\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i;2)})$的结果取平均，而是将各权重${\mathcal{W}}^{(i)},{\mathcal{W}}^{(i;2)}$ 消减一半后，将产生的结果相加。
$$\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i)};{\mathcal{W}}^{(i;2)})\Rightarrow \mathcal{P}(h^{(i)};\frac{1}{2}{\mathcal{W}}^{(i)})+\mathcal{P}(h^{(i)};\frac{1}{2}{\mathcal{W}}^{(i;2)})$$
假如像求解$\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i)},{\mathcal{W}}^{(i;2)})$这样，$h^{(i)}$ 既有$\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i)})$进行表示，也有$\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i;2)})$进行表示，这种方式看起来是可行的；但是如果像求解$\mathcal{P}(v^{(i)})$或者是$\mathcal{P}(h^{(i;2)})$这种没有前驱/后继结点相关联的随机变量，它们使用系数减半可能并不可取。
由于与这种网络层相关联的结点信息相关联的其他结点仅有唯一一层，如果将这种层的权重信息也减半的话，那么它就真的被减半了，没有其他层进行互补。

因此，需要对整个网络的边缘层结构进行优化。以观测变量层为例：基于上述思想，我们更希望$h^{(i)}\to v^{(i)}$层传递信息时不丢失权重信息，而仅将$v^{(i)}\to h^{(i)}$信息传递的过程权重减半。见下图(局部)：

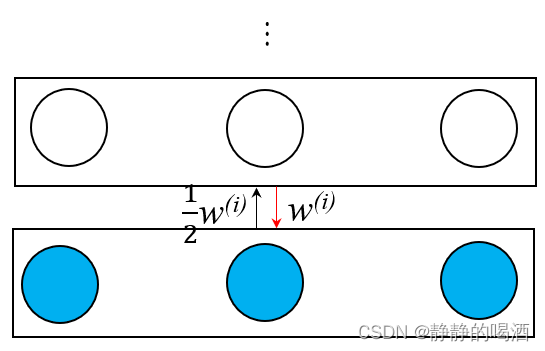
这种操作是容易实现的：
$$\begin{array}{rl}\mathcal{P}(v^{(i)};{\mathcal{W}}^{(i)})& =\sum _{h^{(i)}}\mathcal{P}(v^{(i)},h^{(i)};{\mathcal{W}}^{(i)})\\ & =\sum _{h^{(i)}}\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i)})\cdot \underset{后验概率，Sigmoid函数可精确描述}{\underbrace{\mathcal{P}(v^{(i)}\mid h^{(i)};{\mathcal{W}}^{(i)})}}\\ \mathcal{P}(h^{(i)};\frac{1}{2}{\mathcal{W}}^{(i)})& =\sum _{v^{(i)}}\mathcal{P}(v^{(i)},h^{(i)};\frac{1}{2}{\mathcal{W}}^{(i)})\\ & =\sum _{v^{(i)}}\mathcal{P}(v^{(i)};\frac{1}{2}{\mathcal{W}}^{(i)})\cdot \underset{同样是Sigmoid函数，但权重减半}{\underbrace{\mathcal{P}(h^{(i)}\mid v^{(i)};\frac{1}{2}{\mathcal{W}}^{(i)})}}\end{array}$$
然后，$\mathcal{P}(v^{(i)};{\mathcal{W}}^{(i)})$不再发生变化，关于${\mathcal{W}}^{(i;2)}$表示$h^{(i)}$的边缘概率分布$\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i;2)})$同上，最终将两结果相加，得到最终的边缘概率结果$\mathcal{P}(h^{(i)})$：
$$\begin{array}{rl}\mathcal{P}(h^{(i)};\frac{1}{2}{\mathcal{W}}^{(i;2)})& =\sum _{h^{(i;2)}}\mathcal{P}(h^{(i)},h^{(i;2)};\frac{1}{2}{\mathcal{W}}^{(i;2)})\\ & =\sum _{h^{(i;2)}}\mathcal{P}(h^{(i;2)};\frac{1}{2}{\mathcal{W}}^{(i;2)})\cdot \mathcal{P}(h^{(i)}\mid h^{(i;2)};\frac{1}{2}{\mathcal{W}}^{(i;2)})\\ \mathcal{P}(h^{(i)};{\mathcal{W}}^{(i)},{\mathcal{W}}^{(i;2)})& =\mathcal{P}(h^{(i)};\frac{1}{2}{\mathcal{W}}^{(i)})+\mathcal{P}(h^{(i)};\frac{1}{2}{\mathcal{W}}^{(i;2)})\end{array}$$
使用这种方式去优化受限玻尔兹曼机叠加结构中对不同层结构权重参数的平衡。需要注意的是，这意味着边缘层组成的结构不再是纯粹的受限波尔兹曼机结构了。

这种权重减半的预训练方式去学习深度玻尔兹曼机结构，并没有涉及到大量的数学描述，从权重减半到边缘层优化，都仅仅是很朴素的想法：
$$\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i)},{\mathcal{W}}^{(i;2)})\stackrel{?}{\Leftarrow }\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i)});\mathcal{P}(h^{(i)};{\mathcal{W}}^{(i;2)})$$
这种方式同样被数学证明了，基于权重减半+边缘层优化的深度玻尔兹曼机的预训练方式相比深度信念网络中关于$\mathcal{P}(h^{(i)})$的性能再向上提升一步，从而能够使$\text{ELBO}$值更大。

下一节将介绍生成对抗网络。

相关参考：
深度玻尔兹曼机4-预训练3-小节