第1关:神经网络基本概念
任务描述
本关任务:根据本节课所学知识完成本关所设置的选择题。
相关知识
为了完成本关任务,你需要掌握:1.神经网络基本概念。
神经网络基本概念
-
神经网络由输入层、隐藏层、输出层组成;
-
层与层之间的神经元有连接,而层内之间的神经元没有连接。连接的神经元都有对应的权重;
-
最左边的层叫做输入层,这层负责接收输入数据;
-
最右边的层叫输出层,我们可以从这层获取神经网络输出数据;
-
输入层和输出层之间的层叫做隐藏层。
-
表示相邻两层不同神经元连接的强度叫权重。如果神经元1到神经元2有较大的值,则意味着神经元1对神经元2有较大影响。权重减小了输入值的重要性,对于接近于0的权重,输入的改变不会影响输出的变化;负权重意味着,增加输入而输出会减小。权重决定了输入对输出影响的大小。

上图中的网络一共由3层神经元组成,但实质上只有2层权重,因此我们通常将输入层当做第0层网络,上图我们称其为2层网络(根据输入层、隐藏层、输出层的总数减去1后的数量来命名网络)。
编程要求
请仔细阅读题目,结合相关知识,完成本关的选择题任务。
测试说明
平台会对你的代码进行运行测试,如果实际输出结果与预期结果相同,则通关;反之,则 GameOver。
第1关任务——选择题
上图中的神经网络一共有多少个权重? (C)
A、8
B、12
C、20
D、24
第2关:激活函数
任务描述
本关任务:使用sklearn完成新闻文本主题分类任务。
相关知识
为了完成本关任务,你需要掌握如何使用sklearn提供的MultinomialNB类与文本向量化。
数据简介
本关使用的是20newsgroups数据集,20newsgroups数据集是用于文本分类、文本挖据和信息检索研究的国际标准数据集之一。数据集收集了18846篇新闻组文档,均匀分为20个不同主题(比如电脑硬件、中东等主题)的新闻组集合。
部分数据如下:
From: Mamatha Devineni Ratnam <mr47+@andrew.cmu.edu>Subject: Pens fans reactionsOrganization: Post Office, Carnegie Mellon, Pittsburgh, PALines: 12NNTP-Posting-Host: po4.andrew.cmu.eduI am sure some bashers of Pens fans are pretty confused about the lackof any kind of posts about the recent Pens massacre of the Devils. Actually,I am bit puzzled too and a bit relieved. However, I am going to put an endto non-PIttsburghers relief with a bit of praise for the Pens. Man, theyare killing those Devils worse than I thought. Jagr just showed you whyhe is much better than his regular season stats. He is also a lotfo fun to watch in the playoffs. Bowman should let JAgr have a lot offun in the next couple of games since the Pens are going to beat the pulp out of Jersey anyway. I was very disappointed not to see the Islanders lose the finalregular season game. PENS RULE!!!
其中新闻文本对应的主题标签,已经用0-19这20个数字表示。
文本向量化
由于数据集中每一条数据都是很长的一个字符串,所以我们需要对数据进行向量化的处理。例如,I have a apple! I have a pen!可能需要将该字符串转换成向量如[10, 7, 0, 1, 2, 6, 22, 100, 8, 0, 1, 0]。
sklearn提供了实现词频向量化功能的CountVectorizer类。想要对数据进行向量化,代码如下:
from sklearn.feature_ext\fraction.text import CountVectorizer#实例化向量化对象vec = CountVectorizer()#将训练集中的新闻向量化X_train = vec.fit_transform(X_train)#将测试集中的新闻向量化X_test = vec.transform(X_test)
但是仅仅通过统计词频的方式来将文本转换成向量会出现一个问题:长的文章词语出现的次数会比短的文章要多,而实际上两篇文章可能谈论的都是同一个主题。
为了解决这个问题,我们可以使用tf-idf来构建文本向量,sklearn中已经提供了tf-idf的接口,示例代码如下:
from sklearn.feature_ext\fraction.text import TfidfTransformer#实例化tf-idf对象tfidf = TfidfTransformer()#将训练集中的词频向量用tf-idf进行转换X_train = tfidf.fit_transform(X_train_count_vectorizer)#将测试集中的词频向量用tf-idf进行转换X_test = vec.transform(X_test_count_vectorizer)
MultinomialNB
MultinomialNB是sklearn中多项分布数据的朴素贝叶斯算法的实现,并且是用于文本分类的经典朴素贝叶斯算法。在本关中建议使用MultinomialNB来实现文本分类功能。
在MultinomialNB实例化时alpha是一个常用的参数。
alpha: 平滑因子。当等于1时,做的是拉普拉斯平滑;当小于1时做的是Lidstone平滑;当等于0时,不做任何平滑处理。
MultinomialNB类中的fit函数实现了朴素贝叶斯分类算法训练模型的功能,predict函数实现了法模型预测的功能。
其中fit函数的参数如下:
X:大小为[样本数量,特征数量]的ndarry,存放训练样本Y:值为整型,大小为[样本数量]的ndarray,存放训练样本的分类标签
而predict函数有一个向量输入:
X:大小为[样本数量,特征数量]的ndarry,存放预测样本
MultinomialNB的使用代码如下:
clf = MultinomialNB()clf.fit(X_train, Y_train)result = clf.predict(X_test)
编程要求
填写news_predict(train_sample, train_label, test_sample)函数完成新闻文本主题分类任务,其中:
train_sample:原始训练样本,类型为ndarray;
train_label:训练标签,类型为ndarray;
test_sample:原始测试样本,类型为ndarray。
测试说明
只需返回预测结果即可,程序内部会检测您的代码,预测正确率高于0.8视为过关。
第2关任务——代码题
#encoding=utf8
def relu(x):
'''
x:负无穷到正无穷的实数
'''
#********* Begin *********#
if x<=0:
return 0
else:
return x
#********* End *********#第3关:反向传播算法
任务描述
本关任务:用sklearn构建神经网络模型,并通过鸢尾花数据集中鸢尾花的4种属性与种类对神经网络模型进行训练。我们会调用你训练好的神经网络模型,来对未知的鸢尾花进行分类。
相关知识
为了完成本关任务,你需要掌握:1.神经网络是如何训练,2.前向传播,3.反向传播,4.sklearn中的神经网络。
数据集介绍
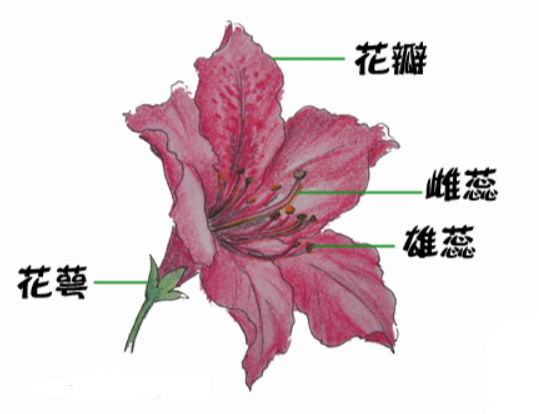
鸢尾花数据集是一类多重变量分析的数据集。通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类。
想要使用该数据集可以使用如下代码:
#获取训练数据train_data = pd.read_csv('./step2/train_data.csv')#获取训练标签train_label = pd.read_csv('./step2/train_label.csv')train_label = train_label['target']#获取测试数据test_data = pd.read_csv('./step2/test_data.csv')
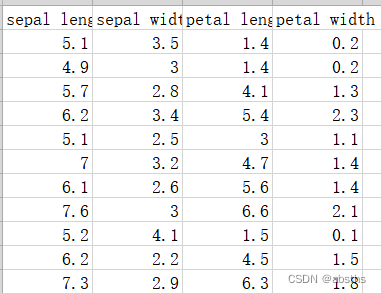
数据集中部分数据与标签如下图所示:

神经网络是如何训练
神经网络的训练方法跟逻辑回归相似:

也是使用梯度下降算法来更新模型的参数,既然要使用梯度下降算法,就要知道损失函数对参数的梯度。在神经网络中,由于有多层的网络,所以使得我们的网络非常不好训练,这么多参数的梯度求起来非常麻烦。反向传播算法出现,为我们解决了这一个问题,它能够快速的计算这些梯度。反向传播算法一共分为两部分:前向传播与反向传播。
前向传播

前向传播指的是数据x从神经网络输入层,与当层的权重相乘,再加上当层的偏置,所得到的值经过激活函数激活后,再输入到下一层。最后,在输出层所得到的值经过softmax函数转化为网络对数据的预测。
Z[1]=XW[1]+B[1]
A[1]=f(Z[1])
Z[2]=A[1]W[2]+B[2]
A=softmax(Z[2])
其中,输出层的Z值要经过softmax函数,转化为预测值。softmax函数公式如下:
ak=sumi=1nexp(zi)exp(zk)
输出层的A为预测值,是一个向量。有多少类别,A就有多长。隐藏层的A[L]为激活值,L代表是第L层隐藏层。W为权重,是一个矩阵,上一层神经网络有多少个神经元,它就有多少行,当层神经网络有多少神经元,它就有多少列。B为偏置,是一个向量,长度与当层神经元个数一样。神经网络使用的损失函数为交叉熵损失函数:
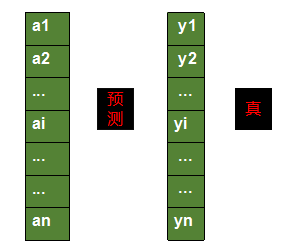
其中ai代表样本被预测为第i个类别的可能性,yi代表样本为第i个类别的真实可能性。交叉熵损失函数公式如下:
L(y,a)=−sumi=1nyilnai
前向传播的主要目的就是得到预测值,再算出交叉熵损失函数。
交叉熵
交叉熵(cross entropy)是深度学习中常用的一个概念,一般用来求目标与预测值之间的差距。机器学习是用网络训练出来的分布q来表示真实分布p,此时当两者的交叉熵越小时,模型训练的结果越接近样本的真实分布,这也是交叉熵被用来作为损失函数的原因。 在机器学习中,P往往用来表示样本的真实分布,比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布,比如[0.7,0.2,0.1]直观的理解就是如果用P来描述样本,那么就非常完美。而用Q来描述样本,虽然可以大致描述,但是不是那么的完美,信息量不足,需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练,也能完美的描述样本,那么就不再需要额外的“信息增量”,Q等价于P。
反向传播
我们通过前向传播能够求出损失函数,而反向传播就是利用前向传播得到的损失函数对参数求梯度,即每个参数的偏导。
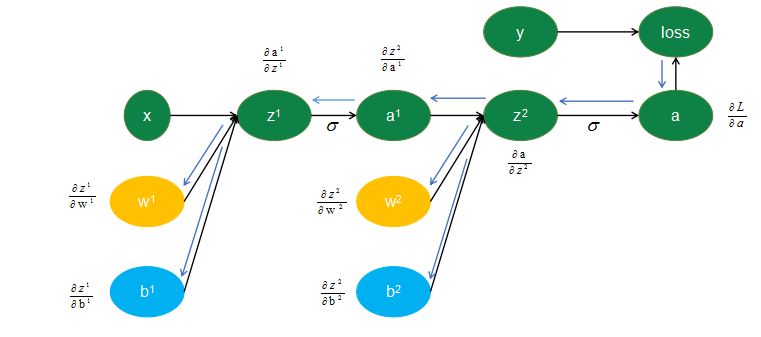
之所以称为反向传播,是因为我们在利用链式法则的时候对各个参数求偏导的传播顺序跟前向传播相反,如我们要求loss对w1的偏导,则要先求出loss对a的偏导,再求出a对z2的偏导,再求出z2对a1的偏导,再求出a1对z1的偏导,再求出z1对w1的偏导,然后全部相乘就得到loss对w1的偏导了。公式如下:
partialw[1]partialloss=partiala[2]partialloss.partialz[2]partiala[2].partiala[1]partialz[2].partialz[1]partiala[1].partialw[1]partialz[1]
所以反向传播的目的就是求出损失函数对各个参数的梯度。最后我们就可以用梯度下降算法来训练我们的神经网络模型了。
sklearn中的神经网络
MLPClassifier的构造函数中有四个常用的参数可以设置:
solver:MLP的求解方法lbfs在小数据上表现较好,adam较为鲁棒,sgd在参数调整较优时会有最佳表现(分类效果与迭代次数);sgd标识随机梯度下降;
alpha:正则项系数,默认为L2正则化,具体参数需要调整;
hidden_layer_sizes:hidden_layer_sizes=(3, 2)设置隐藏层size为2层隐藏层,第一层3个神经元,第二层2个神经元。
max_iter:最大训练轮数。
和sklearn中其他分类器一样,MLPClassifier类中的fit函数用于训练模型,fit函数有两个向量输入:
X:大小为**[样本数量,特征数量]**的ndarray,存放训练样本;
Y:值为整型,大小为**[样本数量]**的ndarray,存放训练样本的分类标签。
MLPClassifier类中的predict函数用于预测,返回预测标签,predict函数有一个向量输入:
X:大小为**[样本数量,特征数量]**的ndarray,存放预测样本。
MLPClassifier的使用代码如下:
from sklearn.neural_network import MLPClassifiermlp = MLPClassifier(solver='lbfgs',max_iter =10,alpha=1e-5,hidden_layer_sizes=(3,2))mlp.fit(X_train, Y_train)result = mlp.predict(X_test)
编程要求
使用sklearn构建神经网络模型,利用训练集数据与训练标签对模型进行训练,然后使用训练好的模型对测试集数据进行预测,并将预测结果保存到./step2/result.csv中。保存格式如下:

测试说明
我们会获取你的预测结果与真实标签对比,预测正确率高于95%视为过关。
第3关任务——代码题
#encoding=utf8
import os
import pandas as pd
if os.path.exists('./step2/result.csv'):
os.remove('./step2/result.csv')
#********* Begin *********#
#获取训练数据
train_data = pd.read_csv('./step2/train_data.csv')
#获取训练标签
train_label = pd.read_csv('./step2/train_label.csv')
train_label = train_label['target']
#获取测试数据
test_data = pd.read_csv('./step2/test_data.csv')
from sklearn.neural_network import MLPClassifier#调用MLP
mlp = MLPClassifier(solver='lbfgs',max_iter =30,
alpha=1e-4,hidden_layer_sizes=(20,))#
mlp.fit(train_data, train_label)
result = mlp.predict(test_data)
save_df = pd.DataFrame({'result':result})
save_df.to_csv('./step2/result.csv',index=0)#保存运行之后会报错,如图所示,报错后把代码全部注释掉再提交就好了
第4关:使用pytorch搭建卷积神经网络识别手写数字
任务描述
本关任务:使用pytorch搭建出卷积神经网络并对手写数字进行识别。
相关知识
为了完成本关任务,你需要掌握:1.卷积神经网络,2.pytorch构建卷积神经网络项目流程。
卷积神经网络
为什么使用卷积神经网络
卷积神经网络最早主要用来处理图像信息。如果用全连接前馈网络来处理图像时,会存在以下两个问题:
参数太多:如果输入图像大小为100 × 100 × 3。在全连接前馈网络中,第一个隐藏层的每个神经元到输入层都有 30000个相互独立的连接,每个连接都对应一个权重参数。随着隐藏层神经元数量的增多,参数的规模也会急剧增加。这会导致整个神经网络的训练效率会非常低,也很容易出现过拟合。局部不变性特征: 自然图像中的物体都具有局部不变性特征,比如在尺度缩放、平移、旋转等操作不影响其语义信息。而全连接前馈网络很难提取这些局部不变特征,一般需要进行数据增强来提高性能。
卷积神经网络是一种具有局部连接、 权重共享等特性的深层前馈神经网络。想要识别图像中的物体,就需要提取出比较好的特征,该特征应能很好地描述想要识别的物体。所以物体的特征提取是一项非常重要的工作。而图像中物体的特征以下几种特点:
1.物体的特征可能只占图像中的一小部分。比如下图中狗的鼻子只是图像中很小的一部分。

2.同样的特征可能出现在不同图像中的不同位置,比如下图中狗的鼻子在两幅图中出现的位置不同。

3.缩放图像的大小对物体特征的影响可能不大,比如下图是缩小后的图,但依然能很清楚的辨认出狗的鼻子。

而卷积神经网络中的卷积与池化操作能够较好地抓住物体特征的以上3种特点。
卷积
卷积说白了就是有一个卷积核(其实就是一个带权值的滑动窗口)在图像上从左到右,从上到下地扫描,每次扫描的时候都会将卷积核里的值所构成的矩阵与图像被卷积核覆盖的像素值矩阵做内积。整个过程如下图所示,其中黄色方框代表卷积核,绿色部分代表单通道图像,红色部分代表卷积计算后的结果,通常称为特征图:
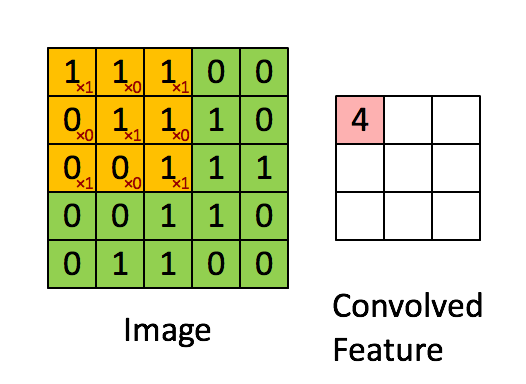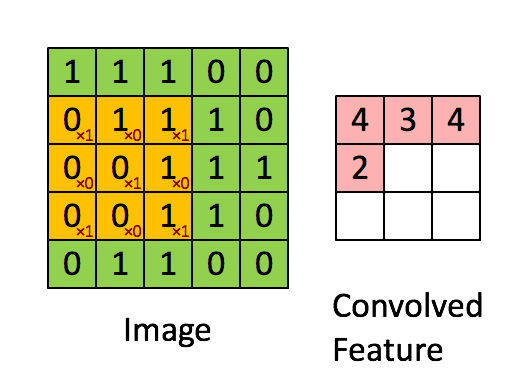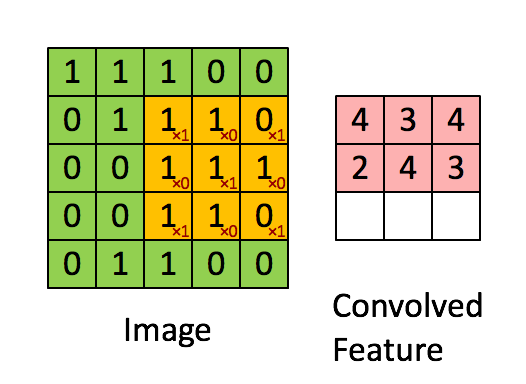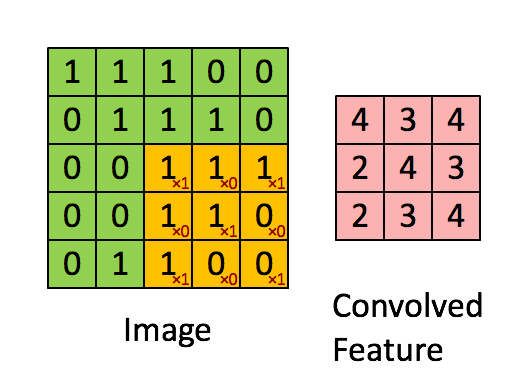
那为什么说卷积能够提取图像中物体的特征呢?其实很好理解,上图中的卷积核中值的分布如下:

当这个卷积核卷积的时候就会在3行3列的小范围内计算出图像中几乎所有的3行3列子图像与卷积核的相似程度(也就是内积的计算结果)。相似程度越高说明该区域中的像素值与卷积核越相似。(上图的特征图中值为4的位置所对应到的源图像子区域中像素值的分布与卷积核值的分布最为接近)这也就说明了卷积在提取特征时能够考虑到特征可能只占图像的一小部分,以及同样的特征可能出现在不同的图像中不同的位置这两个特点。
PS:卷积核的值是怎么确定下来的?很明显是训练出来的!
池化
池化就是将输入图像进行缩小,减少像素信息,只保留重要信息。 池化的操作也很简单,通常情况下,池化区域是2行2列的大小,然后按一定规则转换成相应的值,例如最常用的最大池化(max pooling)。最大池化保留了每一小块内的最大值,也就是相当于保留了这一块最佳的匹配结果。举个例子,如下图中图像是4行4列的,池化区域是2行2列的,所以最终池化后的特征图是2行2列的。图像中粉色区域最大的值是6,所以池化后特征图中粉色位置的值是6,图像中绿色区域最大的值是8,所以池化后特征图中绿色位置的值是8,以此类推。

从上图可以看出,最大池化不仅仅缩小了图像的大小,减少后续卷积的计算量,而且保留了最佳的特征(如果图像是经过卷积后的特征图)。也就相当于把图缩小了,但主要特征还在,这就考虑到了缩放图像的大小对物体的特征影响可能不大的特点。
全连接网络
卷积与池化能够很好的提取图像中物体的特征,当提取好特征之后就可以着手开始使用全连接网络来进行分类了。全连接网络的大致结构如下:
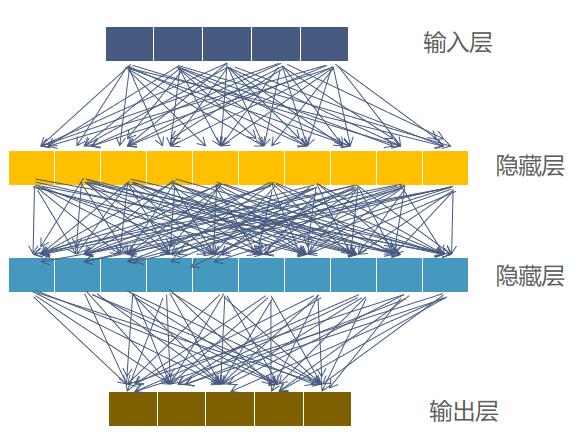
其中输入层通常指的是对图像进行卷积,池化等计算之后并进行扁平后的特征图。隐藏层中每个方块代表一个神经元,每一个神经元可以看成是一个很简单的线性分类器和激活函数的组合。输出层中神经元的数量一般为标签类别的数量,激活函数为softmax(因为将该图像是猫或者狗的得分进行概率化)。因此我们可以讲全连接网络理解成很多个简单的分类器的组合,来构建成一个非常强大的分类器。
卷积神经网络大致结构
将卷积,池化,全连接网络进行合理的组合,就能构建出属于自己的神经网络来识别图像中是猫还是狗。通常来说卷积,池化可以多叠加几层用来提取特征,然后接上一个全连接网络来进行分类。大致结构如下:

pytorch构建卷积神经网络项目流程
数据集介绍与加载数据
本次使用数据集为mnist手写数字数据集,简单来讲就是如下的东西:

数据集分为训练集与测试集,训练集中一共有60000张图片,测试集中一共有10000张图片,每张图片大小为28X28x1。图片标签为对应的数字,如8对应的label为8,若使用onehot编码则对应的label为:[0,0,0,0,0,0,0,0,1,0]。 为节约计算时间,我们取训练集中的6000张图片用来训练,测试集中的600张进行测试。使用pytorch加载数据集方法如下:
#加载数据import torchvisiontrain_data = torchvision.datasets.MNIST(root='./step3/mnist/',train=True, # this is training datatransform=torchvision.transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray todownload=False,)#取6000个样本为训练集train_data_tiny = []for i in range(6000):train_data_tiny.append(train_data[i])train_data = train_data_tiny
构建模型
加载好数据集,就需要构建卷积神经网络模型:
#构建卷积神经网络模型class CNN(nn.Module):def __init__(self):super(CNN, self).__init__()self.conv1 = nn.Sequential( # input shape (1, 28, 28)nn.Conv2d(in_channels=1, # input heightout_channels=16, # n_filterskernel_size=5, # filter sizestride=1, # filter movement/steppadding=2, # if want same width and length of this image after con2d, padding=(kernel_size-1)/2 if stride=1), # output shape (16, 28, 28)nn.ReLU(), # activationnn.MaxPool2d(kernel_size=2), # choose max value in 2x2 area, output shape (16, 14, 14))self.conv2 = nn.Sequential( # input shape (16, 14, 14)nn.Conv2d(16, 32, 5, 1, 2), # output shape (32, 14, 14)nn.ReLU(), # activationnn.MaxPool2d(2), # output shape (32, 7, 7))self.out = nn.Linear(32 * 7 * 7, 10) # fully connected layer, output 10 classesdef forward(self, x):x = self.conv1(x)x = self.conv2(x)x = x.view(x.size(0), -1) # flatten the output of conv2 to (batch_size, 32 * 7 * 7)output = self.out(x)return outputcnn = CNN()
需要指出的几个地方:
class CNN需要继承Module需要调用父类的构造方法:super(CNN, self).__init__()在Pytorch中激活函数Relu也算是一层layer需要实现forward()方法,用于网络的前向传播,而反向传播只需要调用Variable.backward()即可。
定义好模型后还要构建优化器与损失函数: torch.optim是一个实现了各种优化算法的库。使用方法如下:
#SGD表示使用随机梯度下降方法,lr为学习率,momentum为动量项系数optimizer = torch.optim.SGD(model.parameters(), lr = 0.01, momentum=0.9)#交叉熵损失函数loss_func = nn.CrossEntropyLoss()
训练模型
在定义好模型后,就可以根据反向传播计算出来的梯度,对模型参数进行更新,在pytorch中实现部分代码如下:
#将梯度清零optimizer.zero_grad()#对损失函数进行反向传播loss.backward()#训练optimizer.step()
保存模型
在pytorch中使用torch.save保存模型,有两种方法,第一种: 保存整个模型和参数,方法如下:
torch.save(model, PATH)
第二种为官方推荐,只保存模型的参数,方法如下:
torch.save(model.state_dict(), PATH)
加载模型
对应两种保存模型的方法,加载模型也有两种方法,第一种如下:
model = torch.load(PATH)
第二种:
#CNN()为你搭建的模型
model = CNN()
model.load_state_dict(torch.load(PATH))
如果要对加载的模型进行测试,需将模型切换为验证模式
model.eval()
编程要求
使用pytorch搭建出卷积神经网络模型,再对模型进行训练,并将训练好的模型保存至./step3/cnn.pkl中。
测试说明
我们会加载你训练好的模型,并对测试集数据进行预测,预测正确率高于85%视为过关。
提示:平台使用torch版本为0.4,input需要为Variable类型,使用代码如下:
#mini_batchtrain_loader = Data.DataLoader(dataset=train_data, batch_size=64, shuffle=True)
第4关任务——代码题
#encoding=utf8
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.utils.data as Data
import torchvision
import os
if os.path.exists('./step3/cnn.pkl'):
os.remove('./step3/cnn.pkl')
#加载数据
train_data = torchvision.datasets.MNIST(
root='./step3/mnist/',
train=True, # this is training data
transform=torchvision.transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray to
download=False,
)
#取6000个样本为训练集
train_data_tiny = []
for i in range(6000):
train_data_tiny.append(train_data[i])
train_data = train_data_tiny
#********* Begin *********#
train_loader = Data.DataLoader(
dataset=train_data,
batch_size=64,
num_workers=2,
shuffle=True
)
# 构建卷积神经网络模型
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.conv1 = nn.Sequential( # input shape (1, 28, 28)
nn.Conv2d(
in_channels=1, # input height
out_channels=16, # n_filters
kernel_size=5, # filter size
stride=1, # filter movement/step
padding=2,
# if want same width and length of this image after con2d, padding=(kernel_size-1)/2 if stride=1
), # output shape (16, 28, 28)
nn.ReLU(), # activation
nn.MaxPool2d(kernel_size=2), # choose max value in 2x2 area, output shape (16, 14, 14)
)
self.conv2 = nn.Sequential( # input shape (16, 14, 14)
nn.Conv2d(16, 32, 5, 1, 2), # output shape (32, 14, 14)
nn.ReLU(), # activation
nn.MaxPool2d(2), # output shape (32, 7, 7)
)
self.out = nn.Linear(32 * 7 * 7, 10)
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x = x.view(x.size(0), -1)
output = self.out(x)
return output
cnn = CNN()
optimizer = torch.optim.SGD(cnn.parameters(), lr=0.01, momentum=0.9)
loss_func = nn.CrossEntropyLoss()
EPOCH = 3
for e in range(EPOCH):
for x, y in train_loader:
batch_x = Variable(x)
batch_y = Variable(y)
outputs = cnn(batch_x)
loss = loss_func(outputs, batch_y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
#********* End *********#
#保存模型
torch.save(cnn.state_dict(), './step3/cnn.pkl')