同数组元素的插入差不多。
数组元素的插入,是先移动要插入元素位置后面的所有元素,再插入新元素,长度+1。
C语言| 数组的插入-CSDN博客
数组元素的删除,是先删除元素,再把后面的元素往前移动一位,而本程序代码是直接覆盖被删除元素的值。

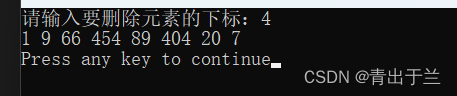
【程序代码】
#include <stdio.h>
int main(void)
{
int a[9] = {1, 9, 66, 454, 33, 89, 404, 20, 7};
int b[8]; //存放删除元素后的数组
int index; //要删除元素的下标
int i;
printf("请输入要删除元素的下标:");
scanf("%d", &index);
for(i=0; i<9; i++)
{
if(i < index)
{
//要删除的下标元素不在数组里面
b[i] = a[i];
}
else
{
//删除值,后面的每一个元素都要往前移动一位,直接覆盖掉删除的元素
b[i] = a[i+1];
}
}
//for循环,输出删除元素后的数组
for(i=0; i<8; i++)
{
printf("%d\x20", b[i]);
}
printf("\n");
return 0;
}


![[stm32]温湿度采集与OLED显示](https://img-blog.csdnimg.cn/direct/1fbb295a14724239a1cb80129cb99756.jpeg)
![[图解]《分析模式》漫谈08-反射·Taylor Swift](https://img-blog.csdnimg.cn/direct/41b1c3e74beb4c8984f3e16937e6d74d.png)