🤵♂️ 个人主页:@艾派森的个人主页
✍🏻作者简介:Python学习者
🐋 希望大家多多支持,我们一起进步!😄
如果文章对你有帮助的话,
欢迎评论 💬点赞👍🏻 收藏 📂加关注+
喜欢大数据分析项目的小伙伴,希望可以多多支持该系列的其他文章
| 大数据分析案例-基于随机森林算法预测人类预期寿命 |
| 大数据分析案例-基于随机森林算法的商品评价情感分析 |
| 大数据分析案例-用RFM模型对客户价值分析(聚类) |
| 大数据分析案例-对电信客户流失分析预警预测 |
| 大数据分析案例-基于随机森林模型对北京房价进行预测 |
| 大数据分析案例-基于RFM模型对电商客户价值分析 |
| 大数据分析案例-基于逻辑回归算法构建垃圾邮件分类器模型 |
| 大数据分析案例-基于决策树算法构建员工离职预测模型 |
| 大数据分析案例-基于KNN算法对茅台股票进行预测 |
| 大数据分析案例-基于多元线性回归算法构建广告投放收益模型 |
| 大数据分案例-基于随机森林算法构建返乡人群预测模型 |
| 大数据分析案例-基于决策树算法构建金融反欺诈分类模型 |
目录
1.项目背景
2.项目简介
2.1研究目的及意义
2.2研究方法与思路
2.3技术工具
3.算法原理
4.项目实施步骤
4.1理解数据
4.2探索性数据分析
4.3数据预处理
4.4特征工程
4.5模型构建
4.6模型评估
5.实验总结
1.项目背景
信用评分是利用数学模型将相关数据转化为某个数值来指导信用决策,是信任的工业化转换。
20世纪30年代,一些邮购公司开始使用数字的评分系统来克服信用分析员在信贷决策中标准不一致的问题(邮购公司存在征信的场景,常常通过先将货物寄出,允许消费者在一段时间后再付款)。
20世纪50年代,美国零售商和邮购商开始应用信用评分。
20世纪60年代末信用卡的诞生,使银行和其它信用卡的发卡机构认识到信用评分的实用性,用来判断借款人是否有能力遵守约定并按时还款。每天申请信用卡的人数之多使得无论从经济上还是人力上,都不得不对发卡决策实行自动化。通过利用计算机技术,这些发卡机构发现,利用信用评分进行发卡决策比任何主观判断都更具有更高预测性,不良率下降了50%以上。
20世纪80年代,信用评分在信用卡中的成功应用使银行开始将评分用于其他产品,例如个人贷款,信用评分也开始在住房抵押贷款和小企业贷款中运用。
信用评分和以下内容紧密相关:
1、 风险评估模型;
2、 数据—客户的信用信息,可来自客户自身、内部系统或征信系统;
3、 风险评估—评估每一笔贷款时,除了信用评分模型,也可参考政策规则和人为判断;
4、 决策规则—指导各类决策行为的策略,包括审批、定价、兑付、催收等。
为什么要用信用评分?
1、对于机构来说,信用评分实现了决策工业化,相比于人为决策大大降低了成本。信用评分在信贷审批时作用最大,同时也在市场营销、账户管理、欠款催收和防范诈骗等领域发挥作用;
2、 对于客户来说,通过信用评分来购买所需的商品和服务,不仅能提高生活品质,也可以满足一些经营的需求。
2.项目简介
2.1研究目的及意义
通过使用python大数据的方法来建立信用评分模型,能提高效率,降低了人为决策的成本。对于金融机构来说,可以根据这个分数决定授信与否,授信额度,利率等。而对于客户来说,通过了解自己的信用分数,可以更好的做出决策。
2.2研究方法与思路
首先使用pandas加载数据并了解数据基本情况,接着使用matplotlib对数据进行可视化,最后使用sklearn拆分数据集为训练和测试集、构建回归模型、评估模型。
2.3技术工具
Python版本:3.9
代码编辑器:jupyter notebook
3.算法原理
线性回归是一个主要影响因素作为自变量来解释因变量的变化,在现实问题研究中,因变量的变化往往受几个重要因素的影响,此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化,这就是多元回归亦称多重回归。当多个自变量与因变量之间是线性关系时,所进行的回归分析就是多元线性回归。 设y为因变量X1,X2…Xk为自变量,并且自变量与因变量之间为线性关系时,则多元线性回归模型为:
Y=b0+b1x1+…+bkxk+e
其中,b0为常数项,b1,b2…bk为回归系数,b1为X1,X2…Xk固定时,x1每增加一个单位对y的效应,即x1对y的偏回归系数;同理b2为X1,X2…Xk固定时,x2每增加一个单位对y的效应,即,x2对y的偏回归系数,等等。如果两个自变量x1,x2同一个因变量y呈线相关时,可用二元线性回归模型描述为:
y=b0 +b1x1 +b2x2 +e
建立多元线性回归模型时,为了保证回归模型具有优良的解释能力和预测效果,应首先注意自变量的选择,其准则是:
(1)自变量对因变量必须有显著的影响,并呈密切的线性相关;
(2)自变量与因变量之间的线性相关必须是真实的,而不是形式上的;
(3)自变量之间应具有一定的互斥性,即自变量之间的相关程度不应高于自变量与因变量之间的相关程度;
(4)自变量应具有完整的统计数据,其预测值容易确定。
4.项目实施步骤
4.1理解数据
导入实验用到的第三方包并加载数据查看前五行
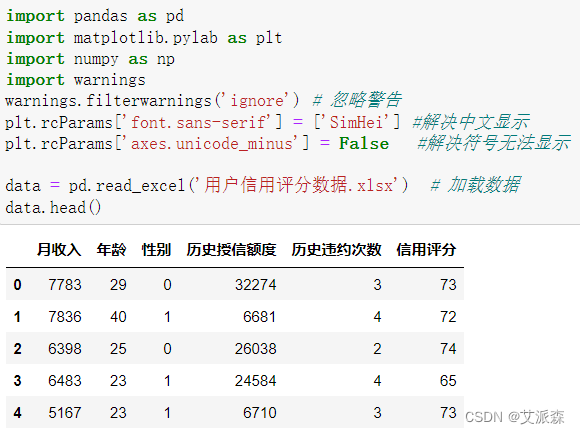
查看数据描述性统计

从描述性统计结果中我们可以看出这六列特征的均值、方差、最大最小值、四分位数等信息。
查看数据基本信息

这六列特征都为整数类型。
4.2探索性数据分析
分析历史违约次数与信用评分之间的相关性

从图中可看出违约次数越高,信用评分越低,两者呈负相关,符合正常逻辑。
分析信用评分的分布情况

从直方图中可看出信用评分主要集中在80-90分,60-80分之间呈正态分布。
4.3数据预处理

在数据预处理这我们删除了缺失值和重复值。
4.4特征工程
我们选取了除了信用评分这一列的其他五个特征为自变量,选取信用评分为因变量,并拆分数据集,其中训练集比例为0.8,测试集比例为0.2。

4.5模型构建
构建线性回归模型并输出模型平均绝对误差

可以看出线性回归模型的平均绝对误差为3.368
构建决策树回归模型并输出模型平均绝对误差

可以看出决策树回归模型的平均绝对误差为4.625,大于线性回归模型的误差,故应选取线性回归模型作为最终训练模型。
4.6模型评估
模型评估选取了R方和均方误差

从结果中看出线性回归模型的均方误差为18.29,模型R方为0.68,模型效果一般。
接着我们选取了前五十的真实值和预测值进行可视化
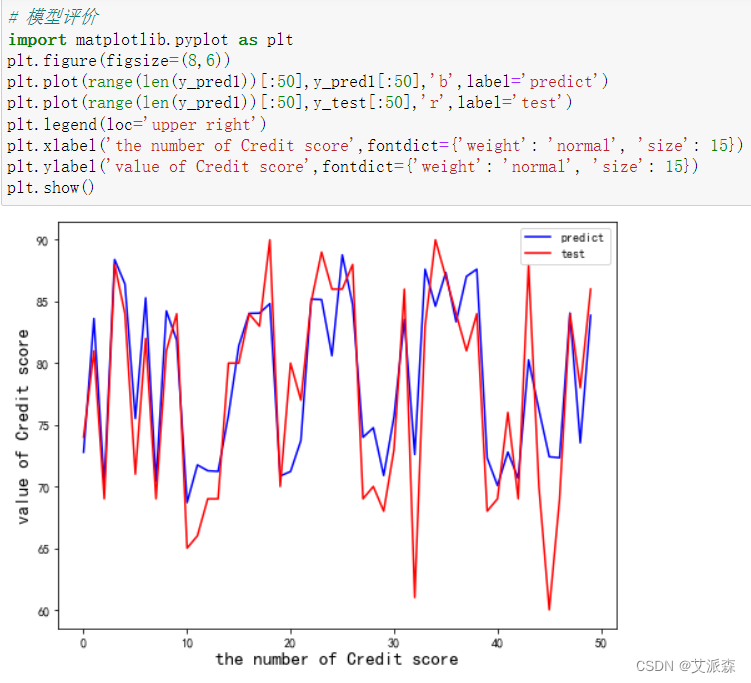
从图中也可看出,预测值和真实值之间还有一定的差距,模型效果还需改善。
5.实验总结
本次实验最后构建的模型为线性回归模型,模型平均绝对误差为3.36,均方误差为18.29,R方为0.68,模型效果一般,还有待提高。
通过这次Python项目实战,我学到了许多新的知识,这是一个让我把书本上的理论知识运用于实践中的好机会。原先,学的时候感叹学的资料太难懂,此刻想来,有些其实并不难,关键在于理解。
在这次实战中还锻炼了我其他方面的潜力,提高了我的综合素质。首先,它锻炼了我做项目的潜力,提高了独立思考问题、自我动手操作的潜力,在工作的过程中,复习了以前学习过的知识,并掌握了一些应用知识的技巧等
在此次实战中,我还学会了下面几点工作学习心态:
1)继续学习,不断提升理论涵养。在信息时代,学习是不断地汲取新信息,获得事业进步的动力。作为一名青年学子更就应把学习作为持续工作用心性的重要途径。走上工作岗位后,我会用心响应单位号召,结合工作实际,不断学习理论、业务知识和社会知识,用先进的理论武装头脑,用精良的业务知识提升潜力,以广博的社会知识拓展视野。
2)努力实践,自觉进行主角转化。只有将理论付诸于实践才能实现理论自身的价值,也只有将理论付诸于实践才能使理论得以检验。同样,一个人的价值也是透过实践活动来实现的,也只有透过实践才能锻炼人的品质,彰显人的意志。
3)提高工作用心性和主动性。实习,是开端也是结束。展此刻自我面前的是一片任自我驰骋的沃土,也分明感受到了沉甸甸的职责。在今后的工作和生活中,我将继续学习,深入实践,不断提升自我,努力创造业绩,继续创造更多的价值。
这次Python实战不仅仅使我学到了知识,丰富了经验。也帮忙我缩小了实践和理论的差距。在未来的工作中我会把学到的理论知识和实践经验不断的应用到实际工作中,为实现理想而努力。
源代码
import pandas as pd
import matplotlib.pylab as plt
import numpy as np
import warnings
warnings.filterwarnings('ignore') # 忽略警告
plt.rcParams['font.sans-serif'] = ['SimHei'] #解决中文显示
plt.rcParams['axes.unicode_minus'] = False #解决符号无法显示
data = pd.read_excel('用户信用评分数据.xlsx') # 加载数据
print(data.head())
# 描述性统计
print(data.describe())
# 数据基本信息
print(data.info())
# 数据预处理
# 删除缺失值
data.dropna(inplace=True)
# 删除重复值
data.drop_duplicates(inplace=True)
# 分析历史违约次数与信用评分之间的相关性
plt.scatter(data['历史违约次数'],data['信用评分'])
plt.title('历史违约次数与信用评分之间的相关性')
plt.xlabel('历史违约次数')
plt.ylabel('信用评分')
plt.show()
# 分析信用评分的分布情况
plt.hist(data['信用评分'])
plt.title('信用评分分布直方图')
plt.show()
# 特征筛选
X = data.drop('信用评分',axis=1)
y = data['信用评分']
# 拆分数据集,测试集比例为0.2
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X, y,test_size=0.2)
# 线性回归模型
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
linear = LinearRegression()
linear.fit(x_train,y_train)
y_pred1 = linear.predict(x_test)
print('模型平均绝对误差为:',mean_absolute_error(y_test,y_pred1))
# 决策树回归模型
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_absolute_error
tree = DecisionTreeRegressor()
tree.fit(x_train,y_train)
y_pred2 = tree.predict(x_test)
print('模型平均绝对误差为:',mean_absolute_error(y_test,y_pred2))
# 模型评估
from sklearn.metrics import r2_score,mean_squared_error
print('线性回归模型的均方误差为:',mean_squared_error(y_test,y_pred1))
print('线性回归模型的R方为:',r2_score(y_test,y_pred1))
# 模型评价
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
plt.plot(range(len(y_pred1))[:50],y_pred1[:50],'b',label='predict')
plt.plot(range(len(y_pred1))[:50],y_test[:50],'r',label='test')
plt.legend(loc='upper right')
plt.xlabel('the number of Credit score',fontdict={'weight': 'normal', 'size': 15})
plt.ylabel('value of Credit score',fontdict={'weight': 'normal', 'size': 15})
plt.show()