聚类问题概述：把样本划分为由相似的对象组成的多个类的过程。

K均值聚类算法和K均值++聚类算法

K均值聚类算法流程：

1. 指定需要划分的簇的个数K。
2. 随机选择K个数据对象作为初始的聚类中心（不一定是样本点）。
3. 计算其他的各个数据对象到这K个聚类中心的距离，把数据对象划分到距离它最近的它最近的中心所在的簇中；
4. 调整新类并更新该簇的聚类中心。
5. 循环过程三四，直到聚类中心收敛（不变）或达到最大迭代次数。

K均值算法的优点：算法简单且快速，对于大数据集该算法的效率是很高的。

K均值算法的缺点：

• 必须由使用者事先给出需要生产的簇的个数K；
• 对初值非常敏感；
• 对于孤立点数据敏感。

K均值++算法概述：K均值++算法是K均值算法的改进，只修改了初始化聚类中心的过程，可以避免K均值算法的后面两个缺点。

K均值++算法选择初始聚类中心的基本原则：初始聚类中心之间的相互距离要尽可能的远。

K均值++算法初始化聚类中心的过程：

1. 随机选择一个样本作为第一个聚类中心；
2. 计算每个样本与当前已有聚类中心的最短距离，这个值越大，表示被选为下一个聚类中心的概率越大，最后用轮盘法选出下一个聚类中心。
3. 重复上一个步骤直到选出K个聚类中心。

SPSS使用K均值++算法进行聚类的步骤：

1.打开SPSS软件并导入数据，依次点击：分析→分类→K均值聚类

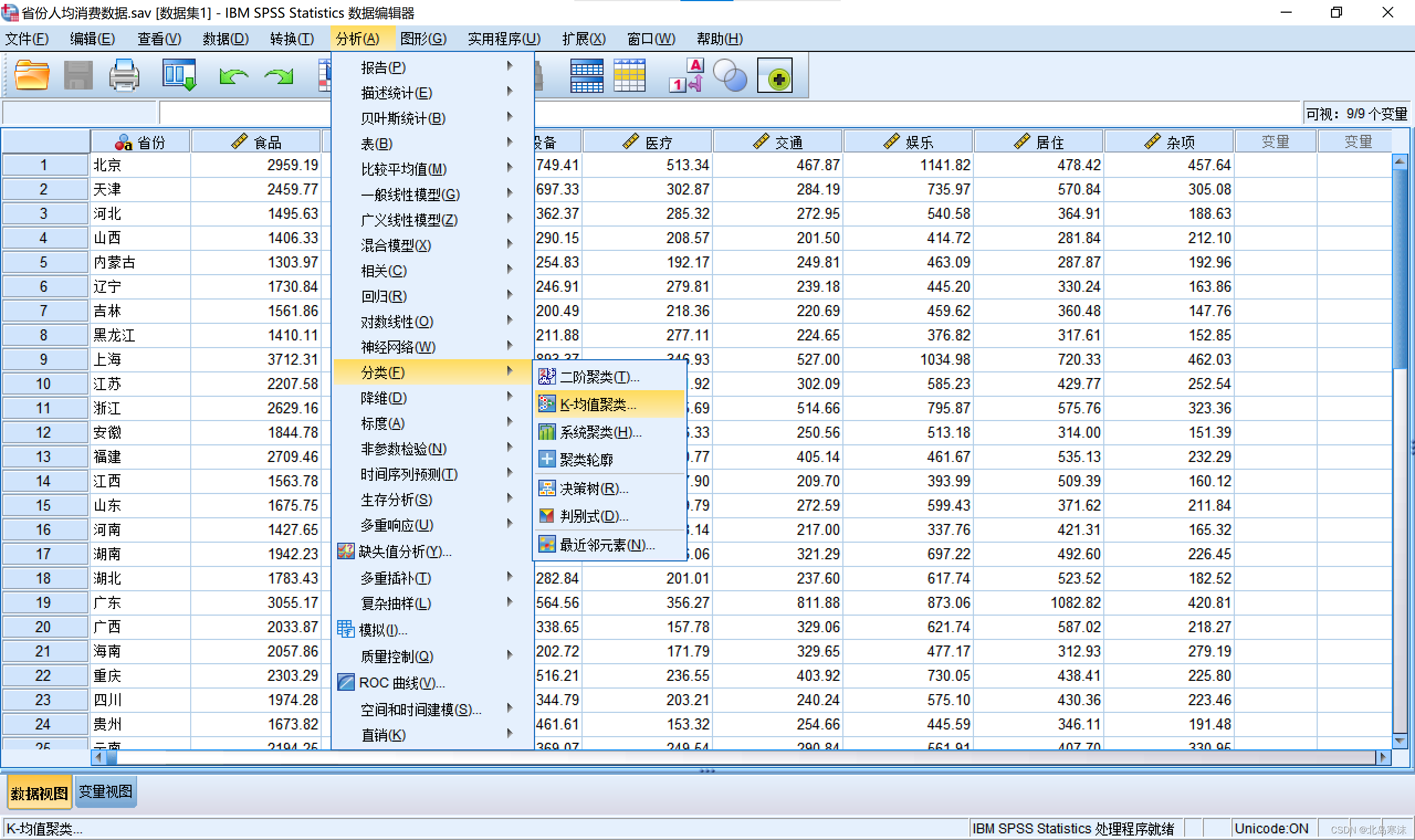
2.添加自变量和聚类的标签变量，并指定聚类生成的簇的个数（默认为2）

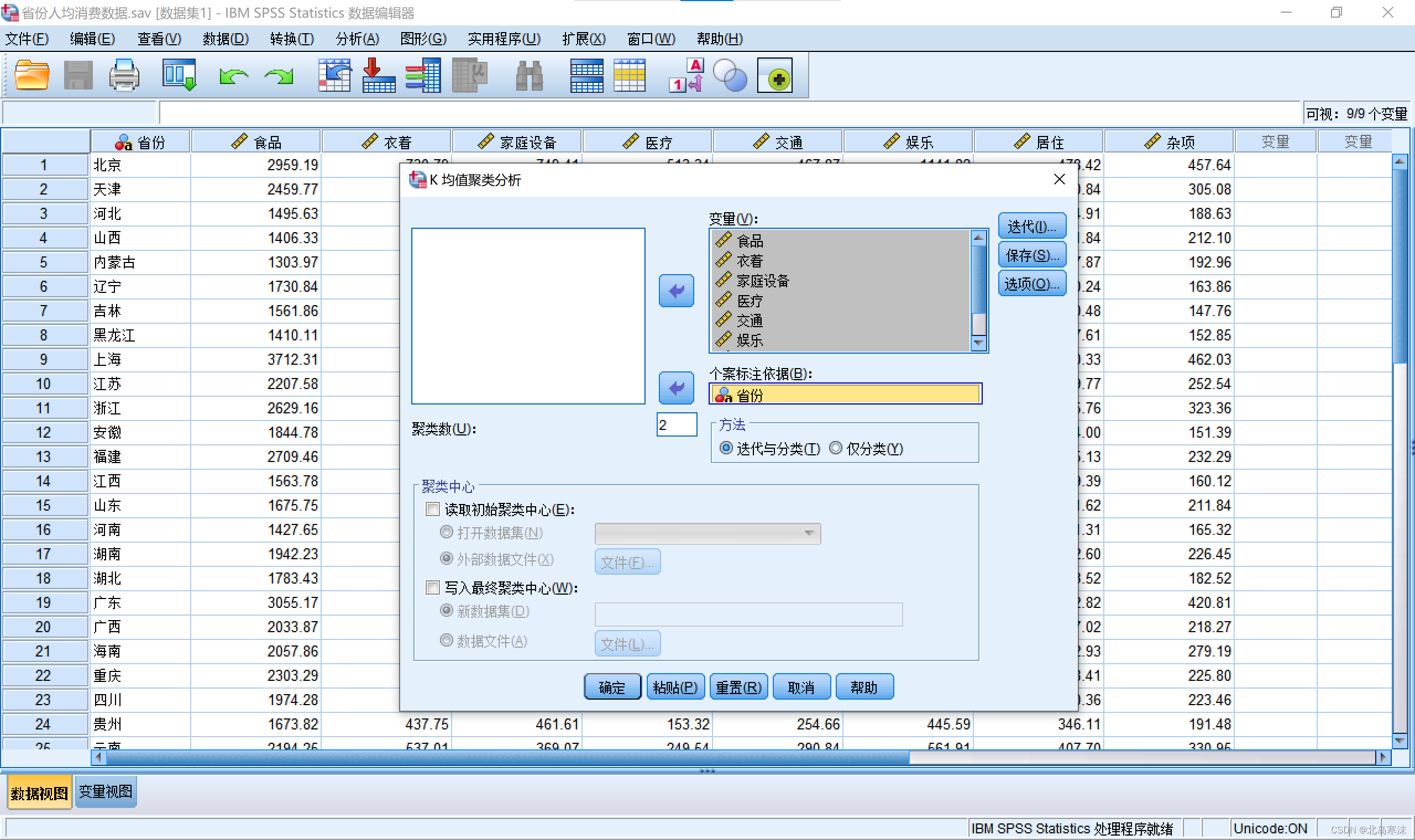
3.在“迭代”按钮菜单中可以调整最大迭代次数（迭代次数过少可能会影响聚类结果）

4.在“保存”按钮菜单中同时勾选聚类成员和与聚类中心的距离。

5.在“选项”按钮菜单中勾选初始聚类中心和每个个案的聚类信息。

SPSS进行K均值++聚类的结果分析：

• 初始聚类中心：

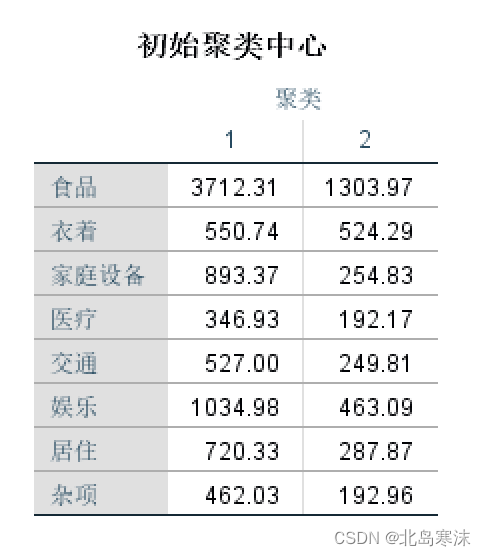
• 最终聚类中心：

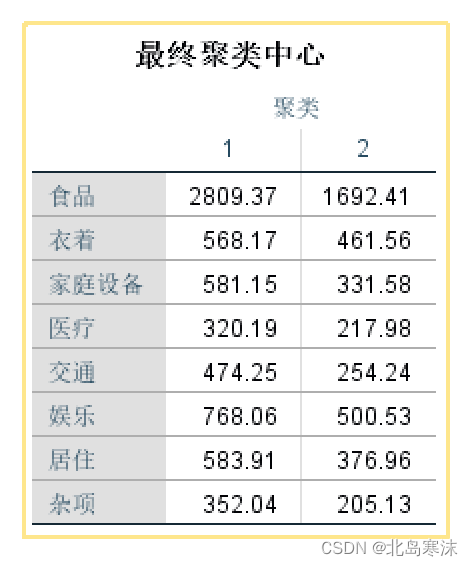
• 最终聚类中心之间的距离：

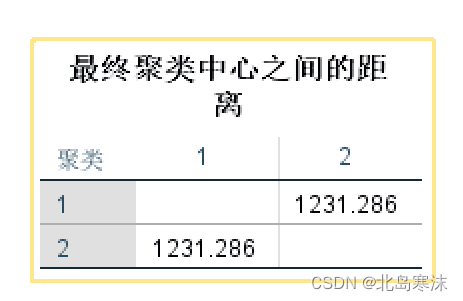
• 每个聚类中的个案数目：

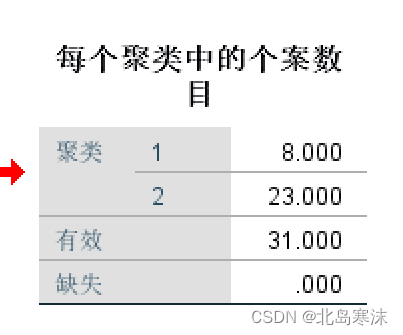
• 聚类结果：

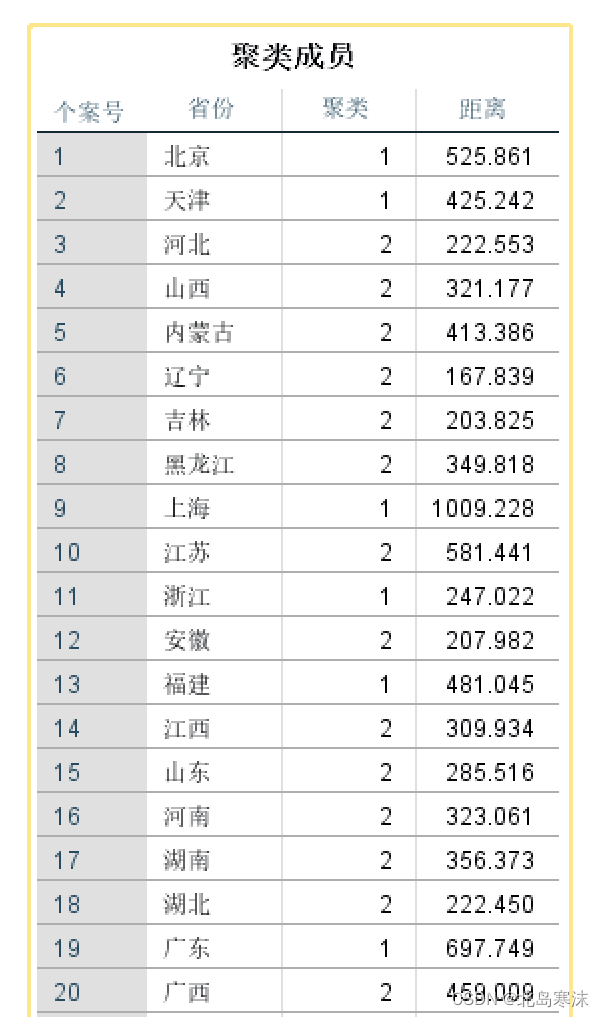
K均值聚类的簇个数如何确定：通常都会多取几个K值，看一看分为几个簇会更好解释。

K均值算法注意事项：K均值聚类使用之前需要对数据进行去量纲化处理，常使用标准化。

使用SPSS进行数据标准化的方法：

1.依次点击：分析→描述统计→描述

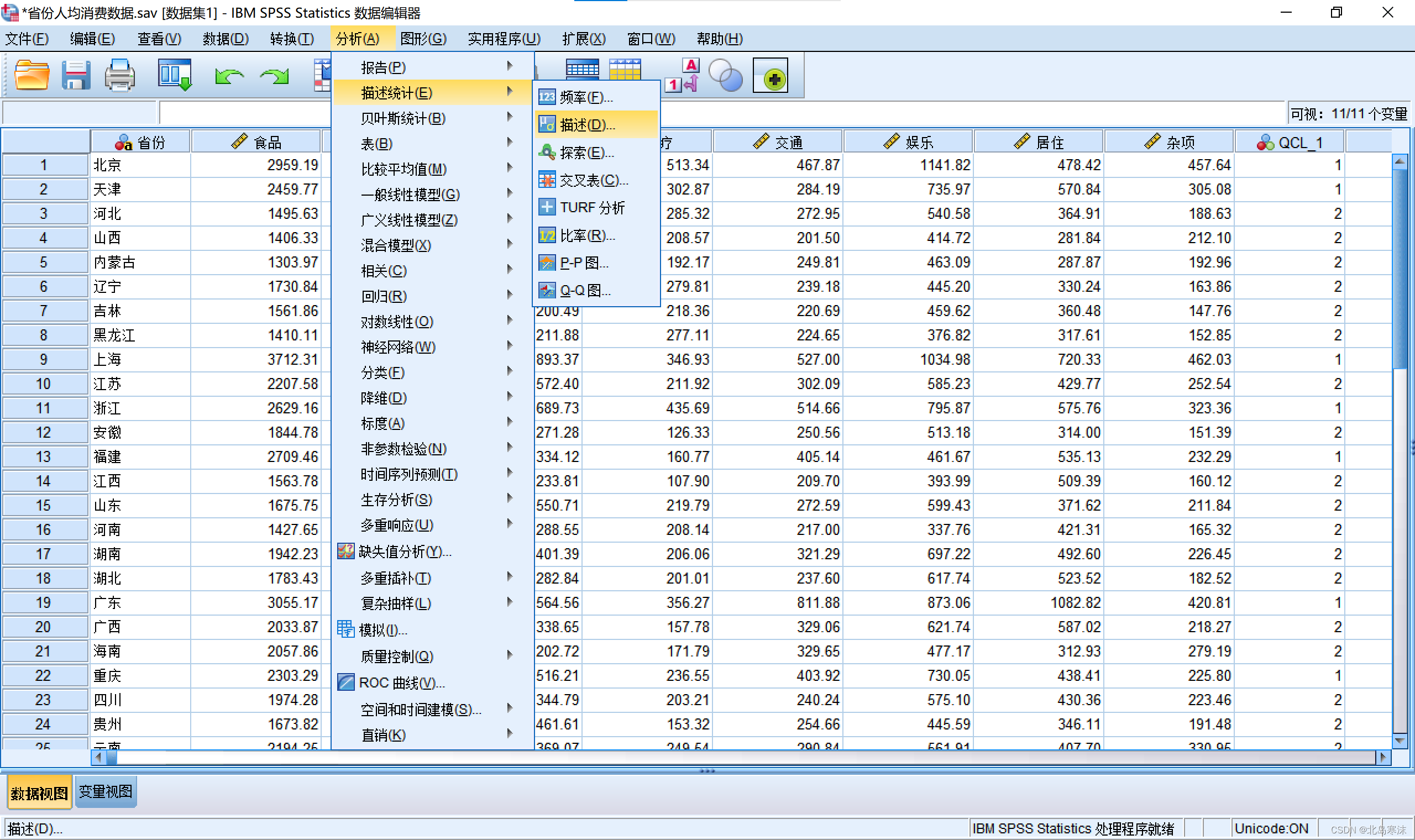
2.选择需要进行标准化的属性，并勾选“将标准化值另存为变量”。

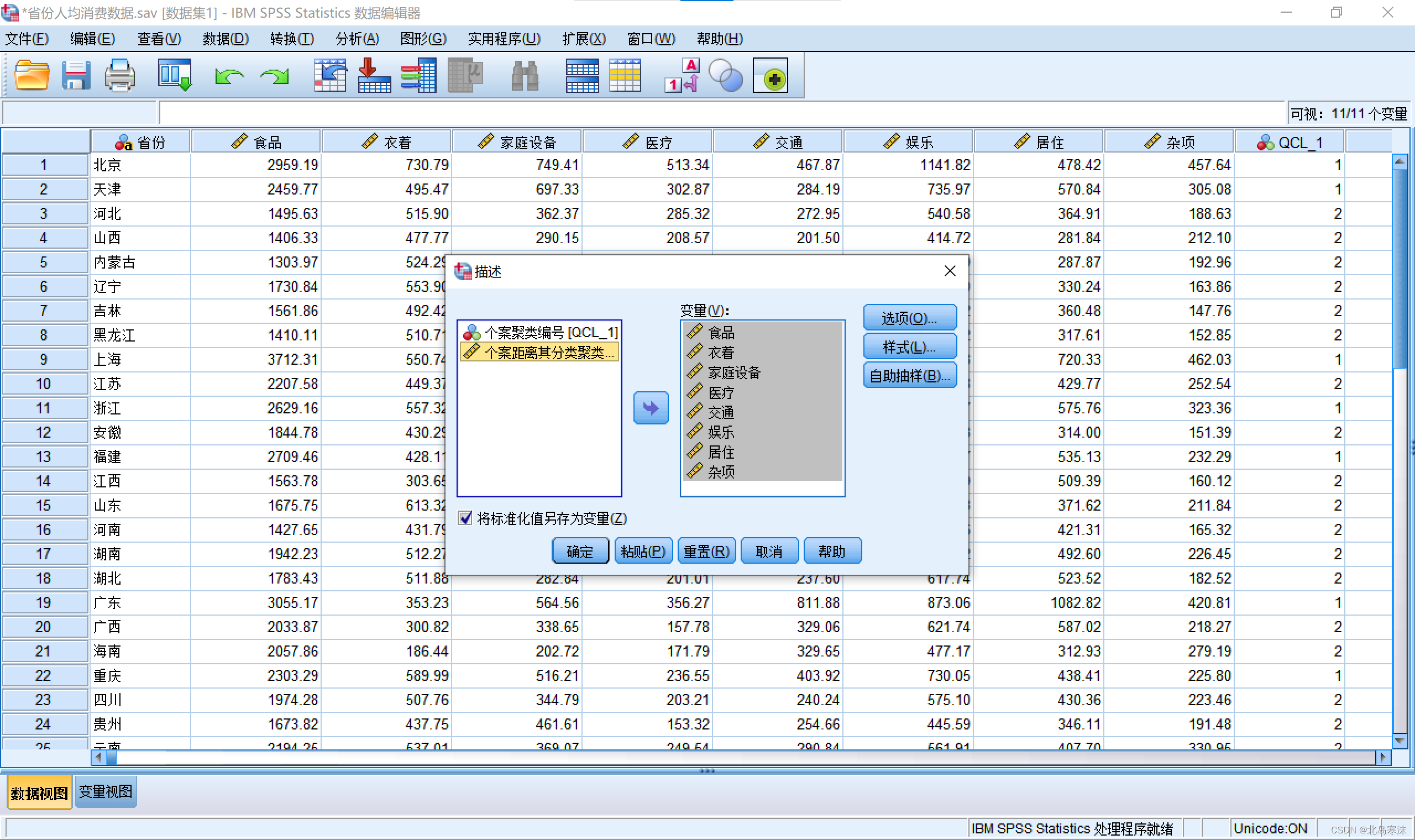
系统聚类算法（层次聚类）

样本间距离的常用类型：

• 曼哈顿距离（绝对值距离）；
• 欧氏距离；
• 闵可夫斯基距离（曼哈顿距离和欧氏距离的推广）；
• 切比雪夫距离；
• 马氏距离。

系统聚类法的算法流程：

1. 写出样本之间的距离矩阵。
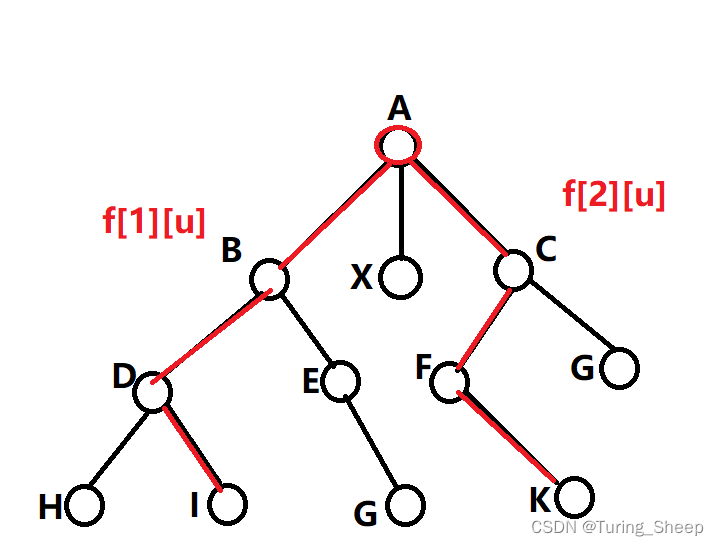
2. 将每一个样本视为一个类，将两两之间距离最小的两个样本聚成一类，更新这个类的聚类中心。并得到新的距离矩阵。
3. 重复上述过程，直到最后只剩下一个簇。

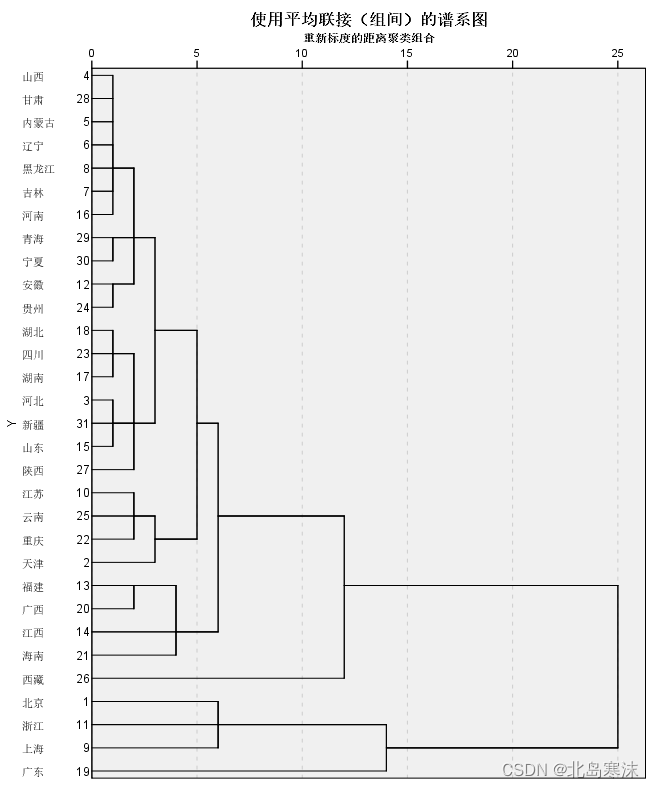
谱系图：谱系图是系统聚类的结果，可以根据谱系图选择最合适的聚类个数。

注意事项：使用系统聚类之前也需要对数据进行去量纲化处理。

使用SPSS进行系统聚类的步骤：

1.打开SPSS软件并导入数据，依次点击：分析→分类→系统聚类

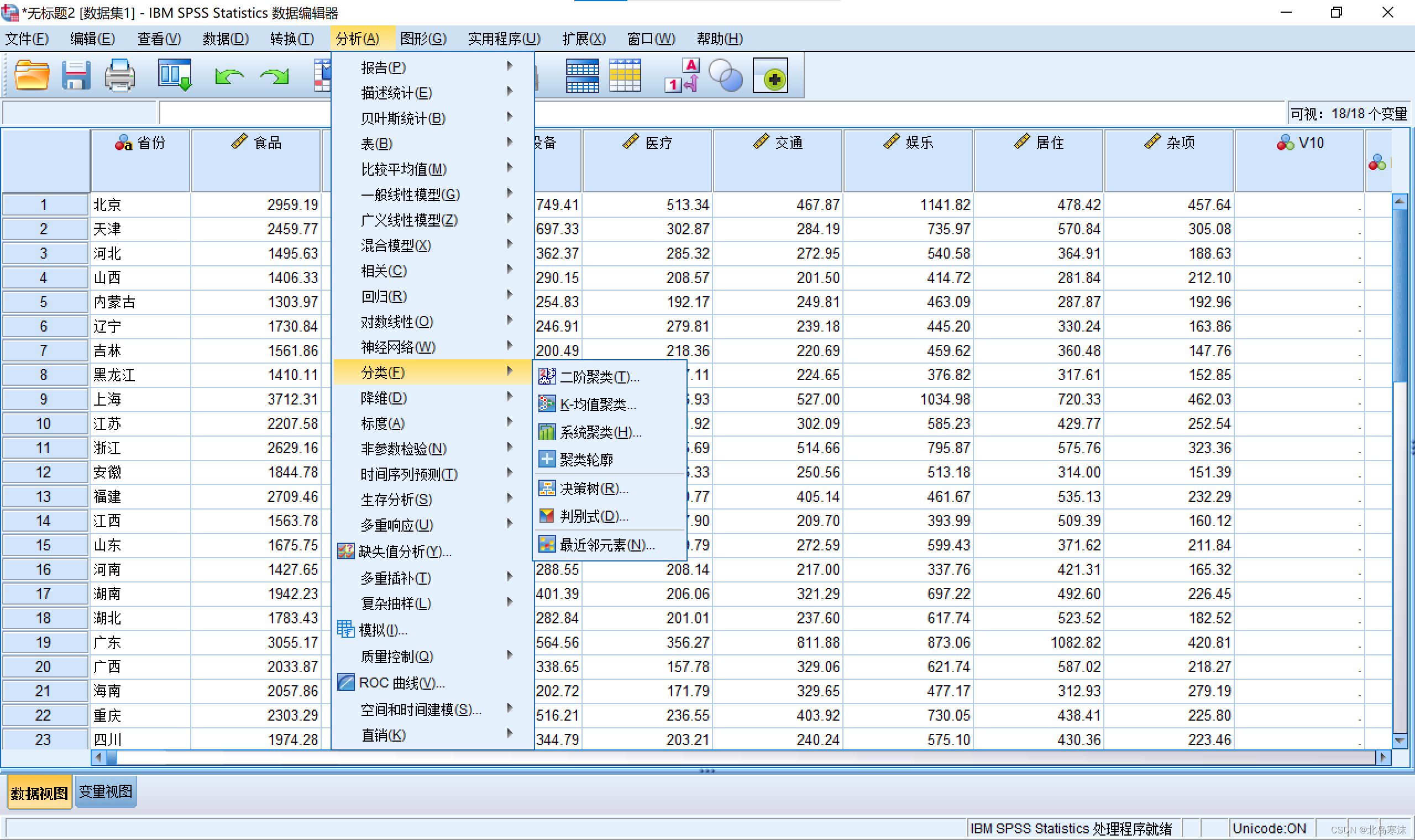
2.导入自变量和分类依据变量。

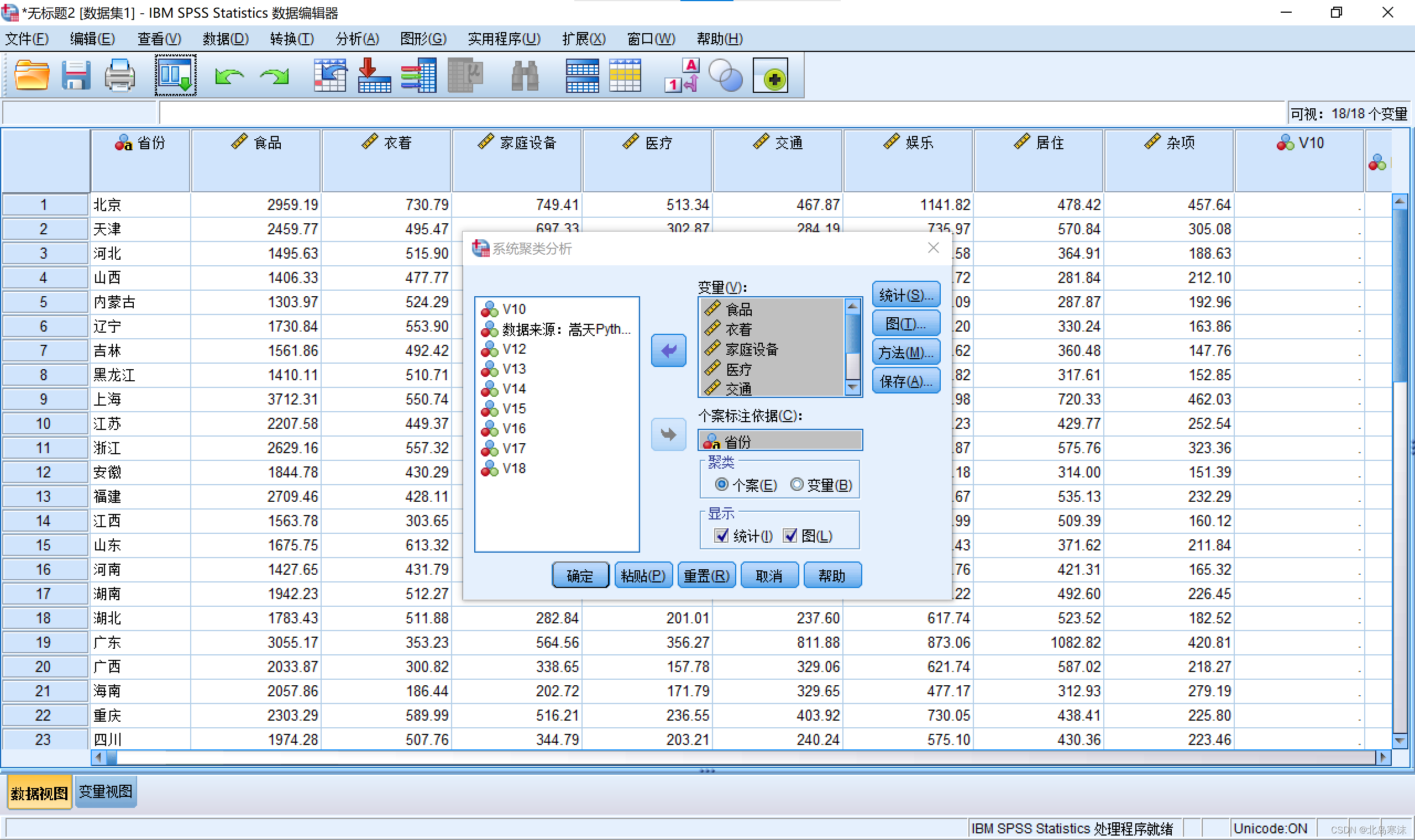
3.在“图”按钮菜单中勾选谱系图。（冰柱图使用较少）

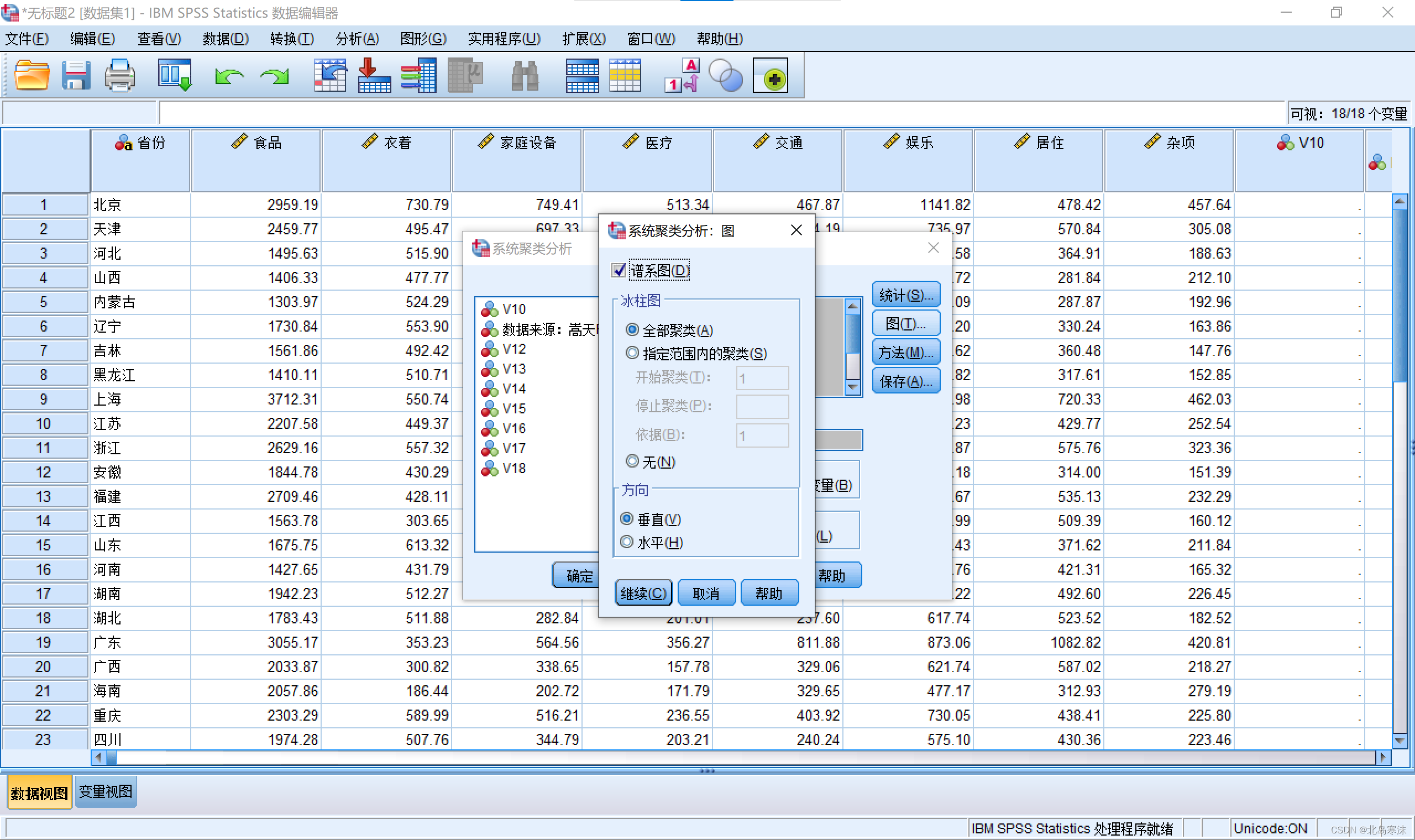
4.在“方法”按钮菜单中可以选择类与类之间的距离计算方式和点与点之间的距离计算方式。同时，如果原始数据量纲不统一，可以在左下方的转换值处对数据进行标准化。

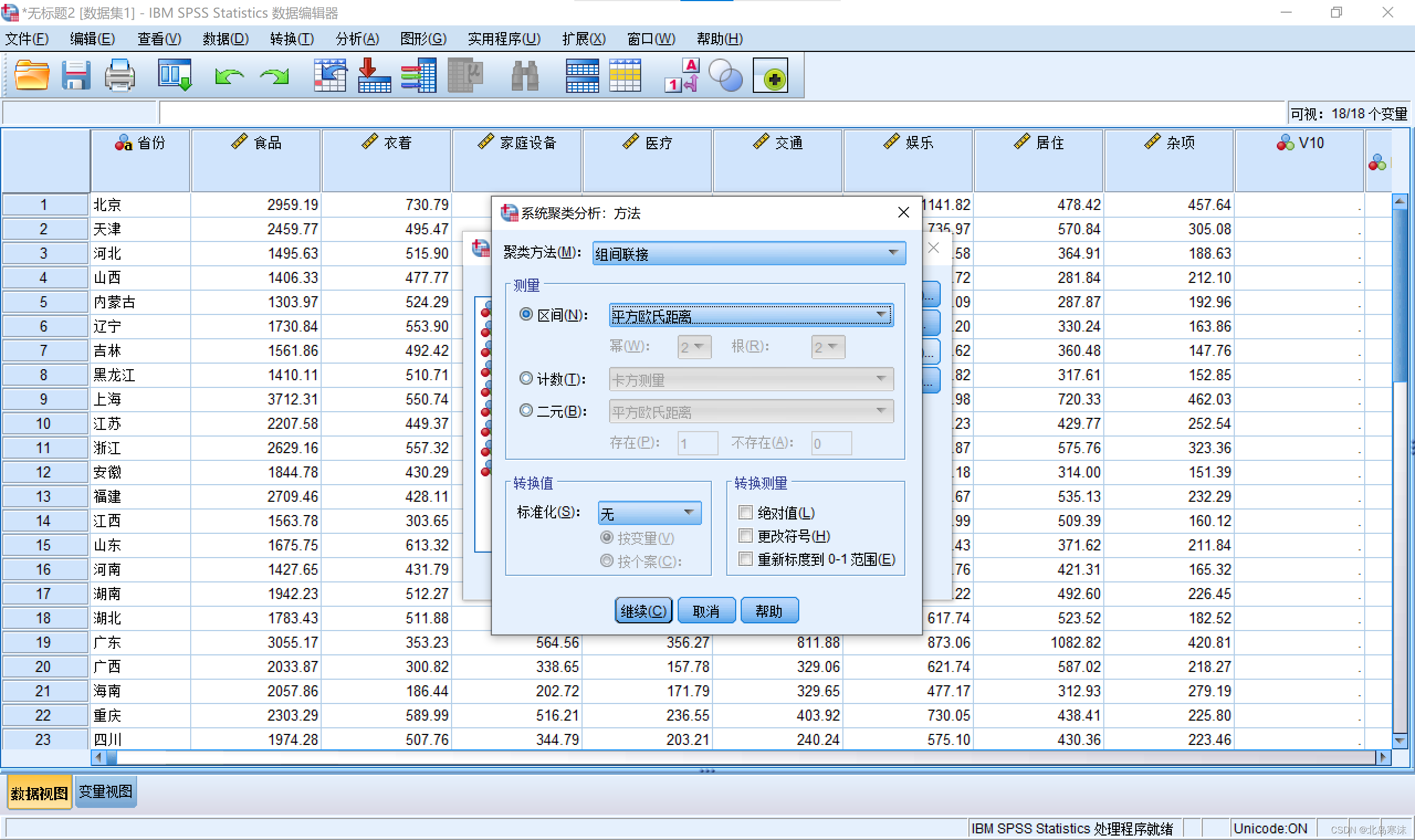
5.通过“肘部法则”等方式确定聚类个数后，重新进行一次系统聚类过程。打开系统聚类窗体后打开“保存”按钮菜单，选择单个解，并输入解的个数。

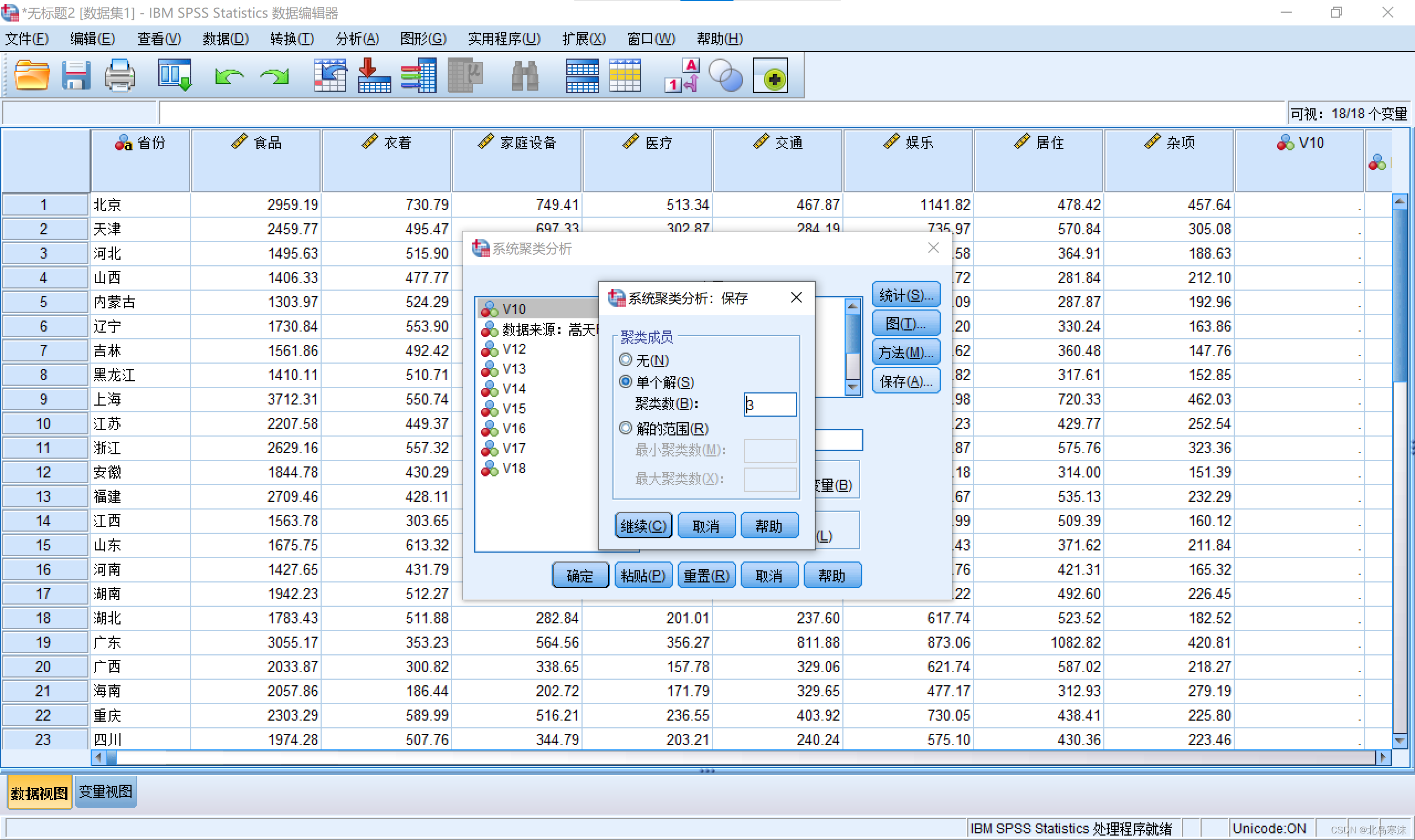
SPSS进行系统聚类的结果：

• 谱系图：
  
• 集中计划表：表格中的系数列经过倒序后可以用于绘制聚合系数折线图。
  

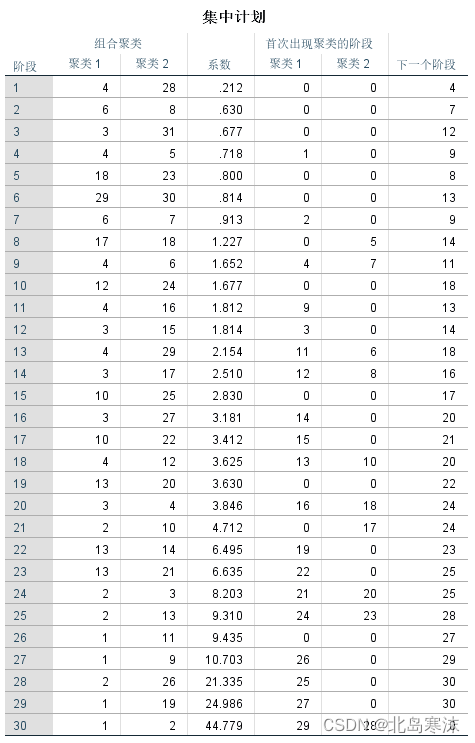
聚合系数：所有样本点离各自的聚类中心距离的平方和，也称为聚合系数，聚类个数越多则聚合系数越小。

聚合系数折线图：聚合系数随着聚类个数变化情况的曲线图。

选择最佳聚类个数（肘部法则）：选择在聚合系数折线图中下降趋势开始变缓且方便解释的点。

SPSS进行聚类结果图的绘制步骤：

• 注意事项：只有指标为二维或三维才能绘图，否则无法绘图，或者需要使用降维算法后再绘图。

1.依次点击：图形→图表构造器

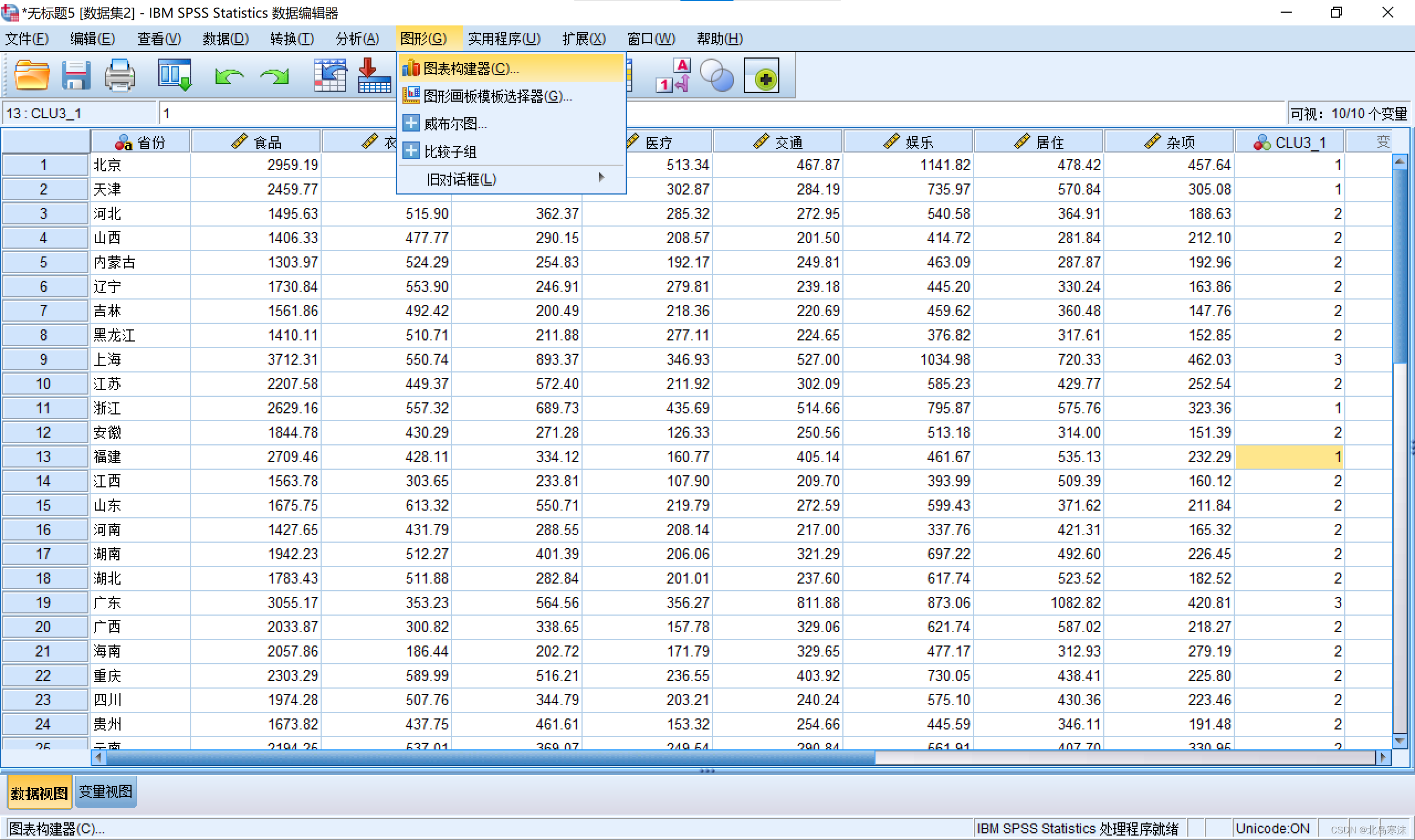
2.在窗口下方选择 散点图与点图，并根据指标个数是两个还是三个选择第三种或第五种图形样式。

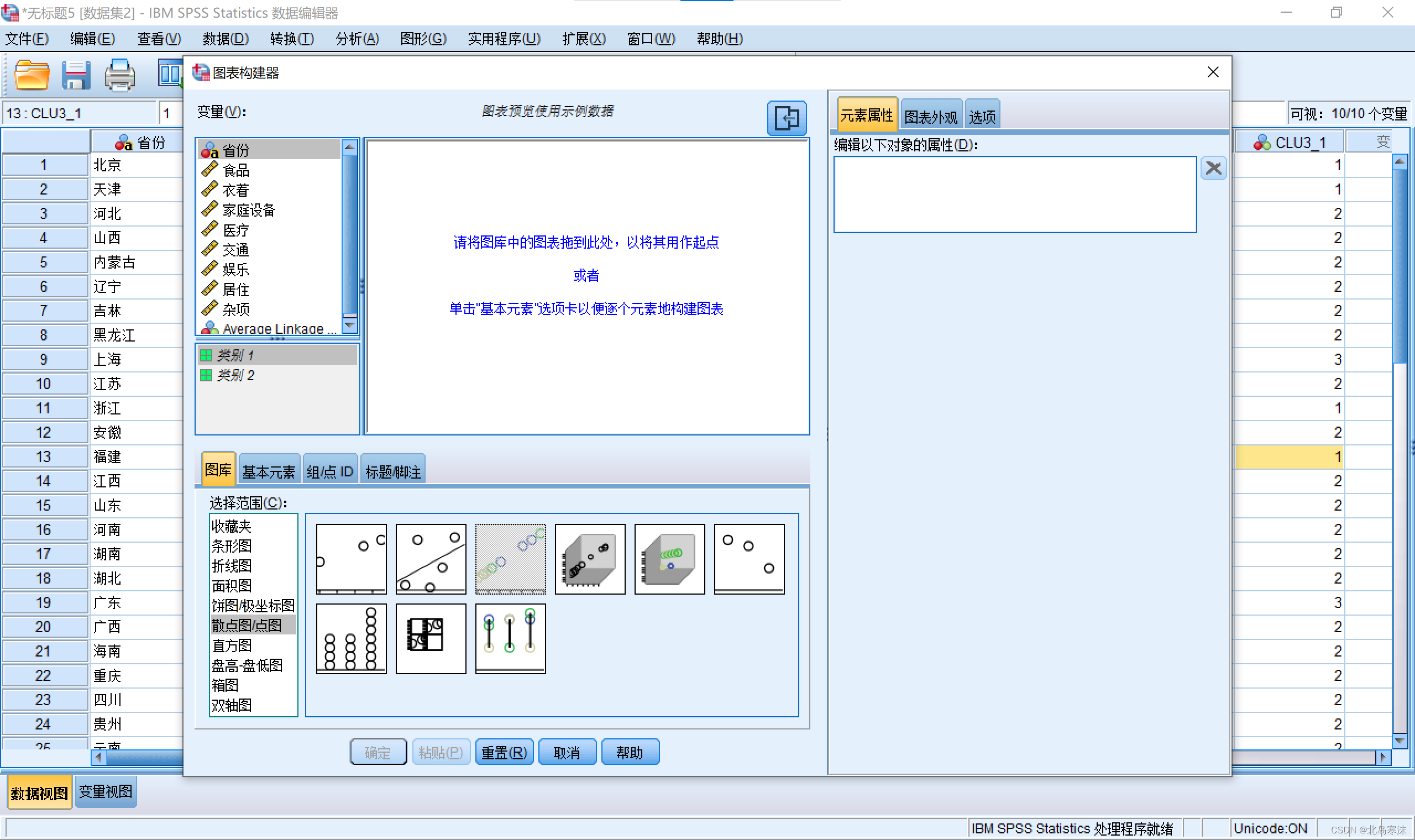
3.选择适当的散点图拖动到左上方，并设置横纵坐标。

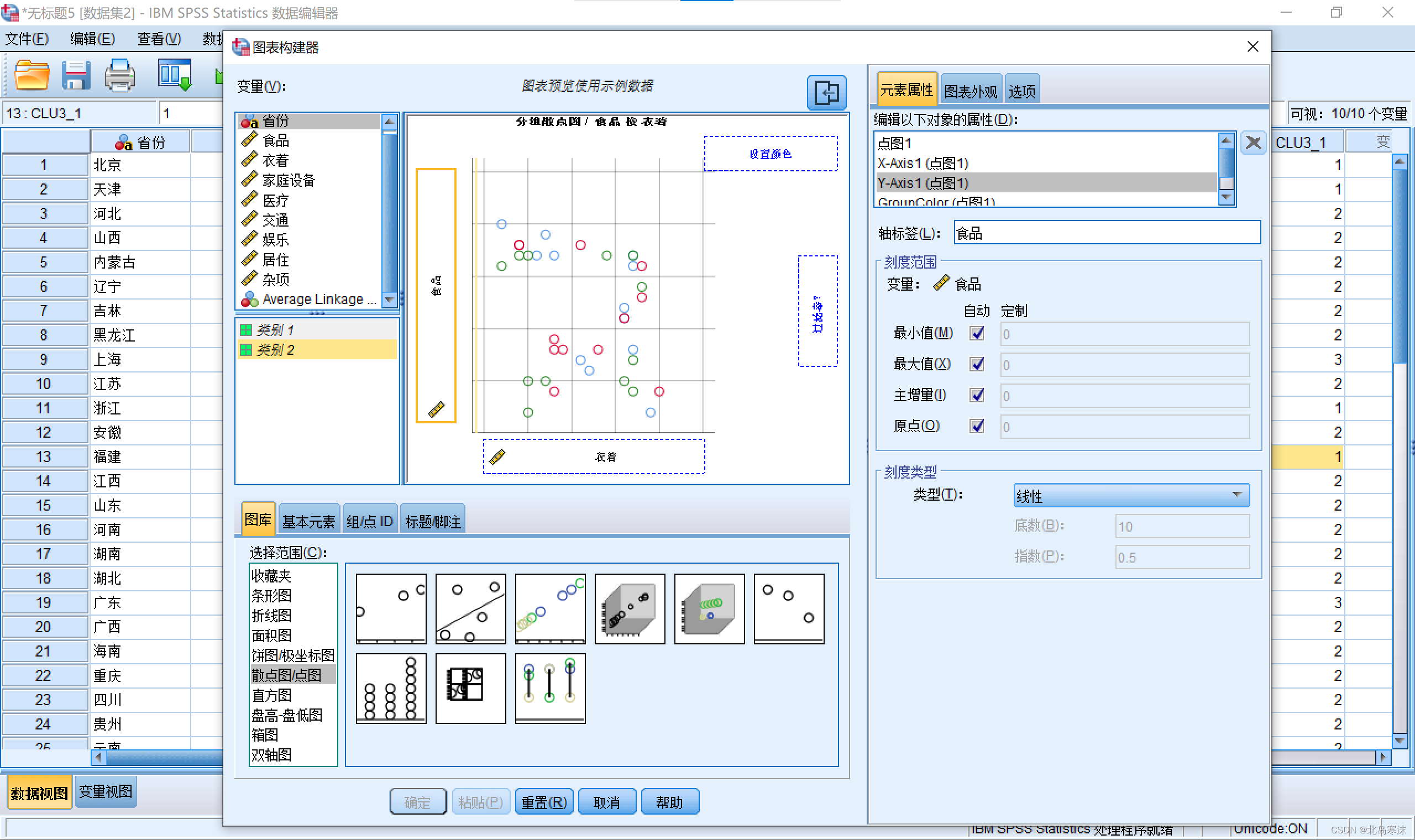
4.在“设置颜色”处选择类别划分的依据为SPSS进行聚类的结果列。

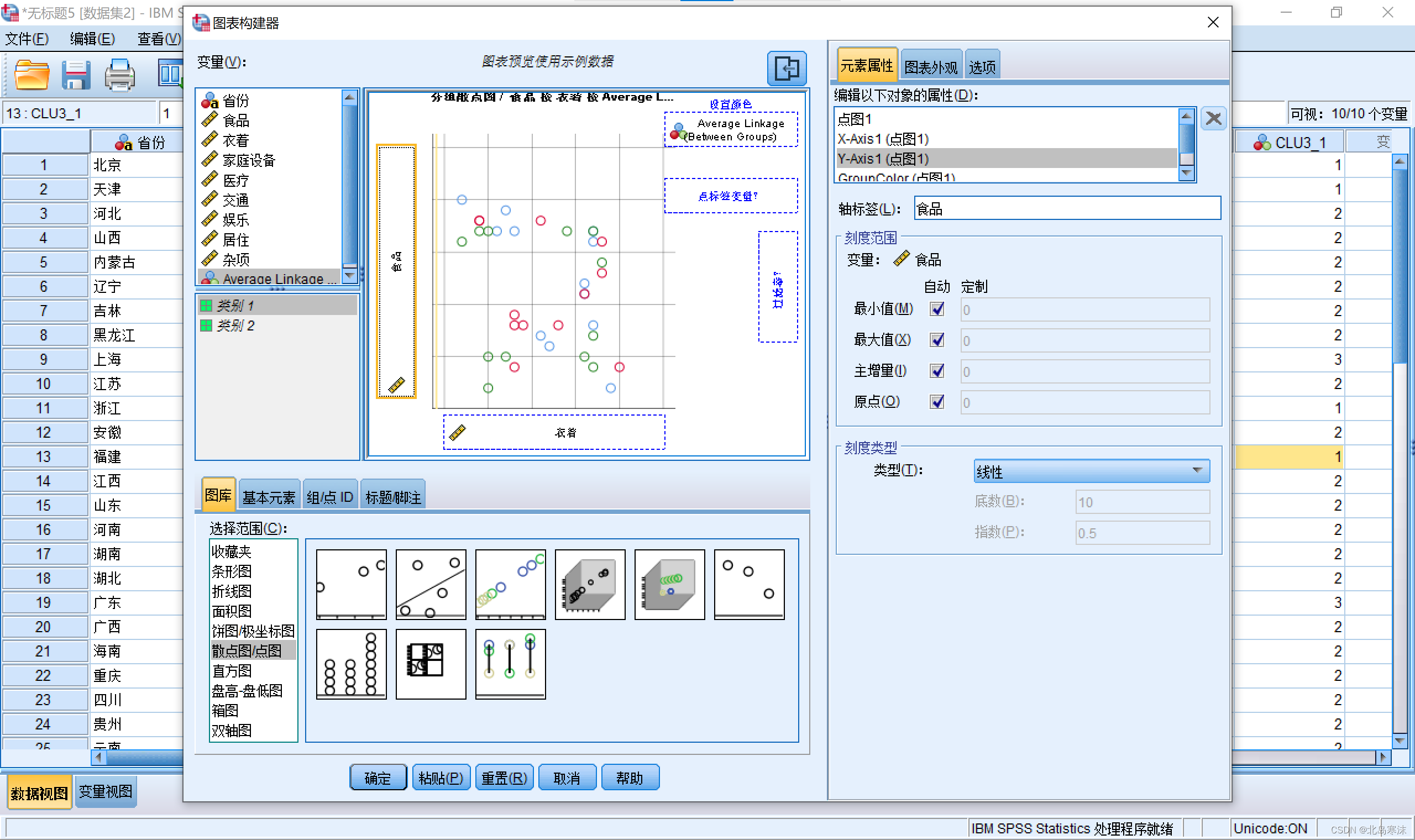
5.在组/点ID标签下，勾选点ID标签。并用拖动的方式设置点标签变量。

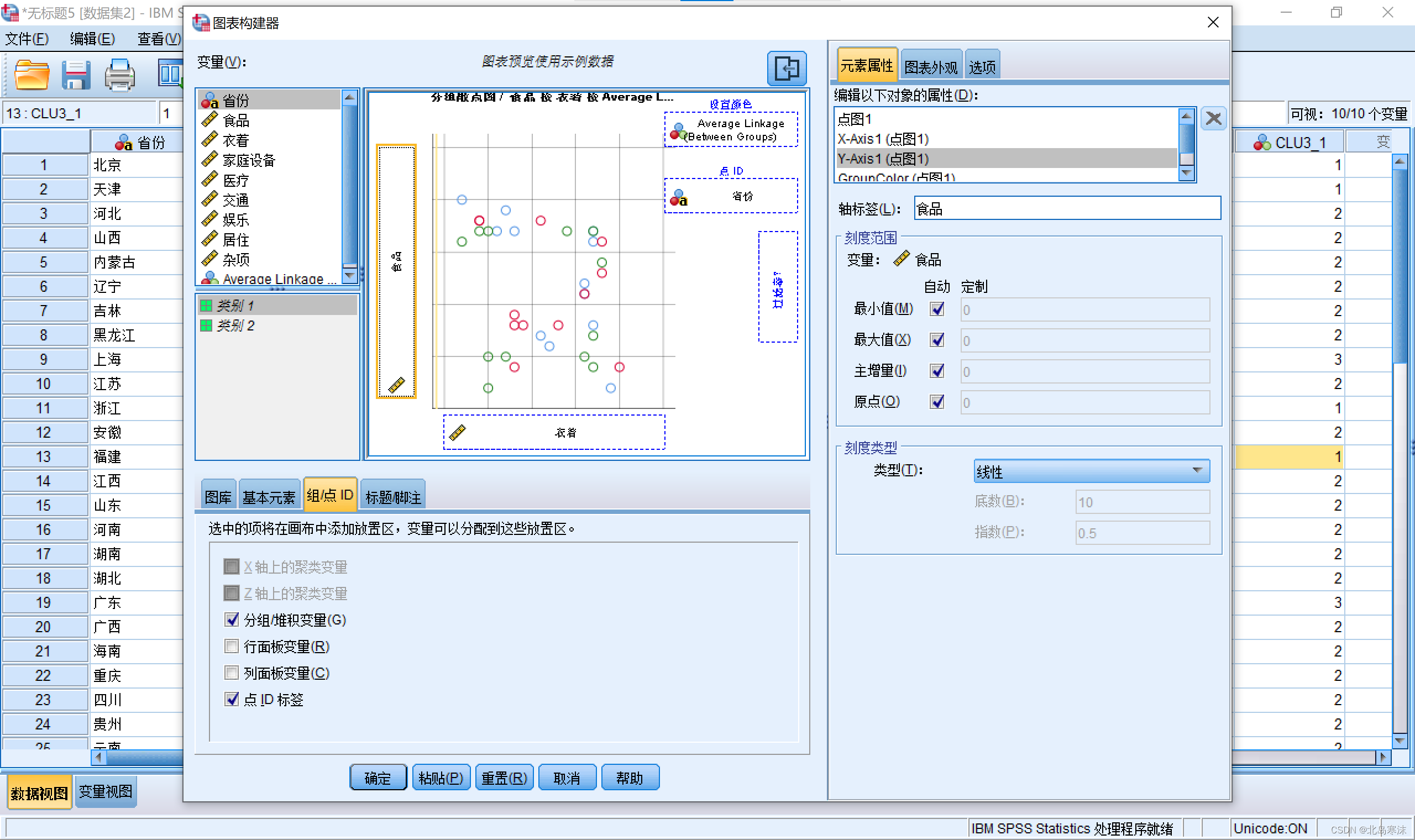
6.双击进入绘图结果，可以修改坐标点的填充色，修改背景颜色，修改图例名称等。

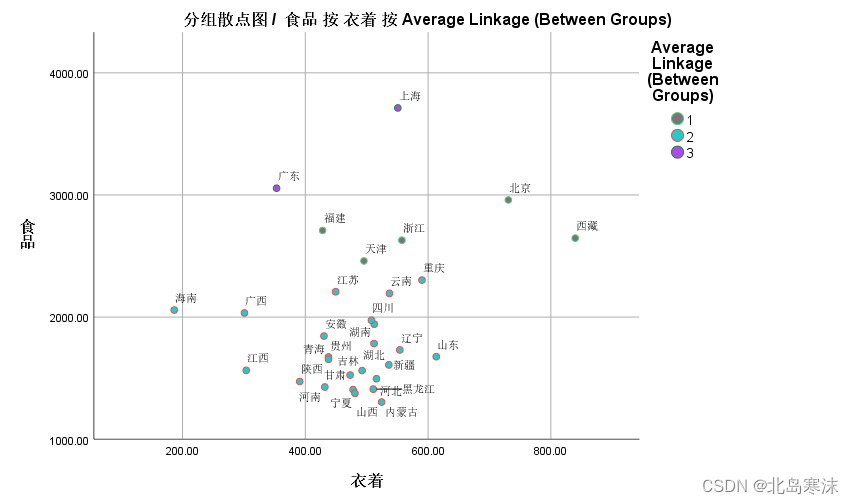
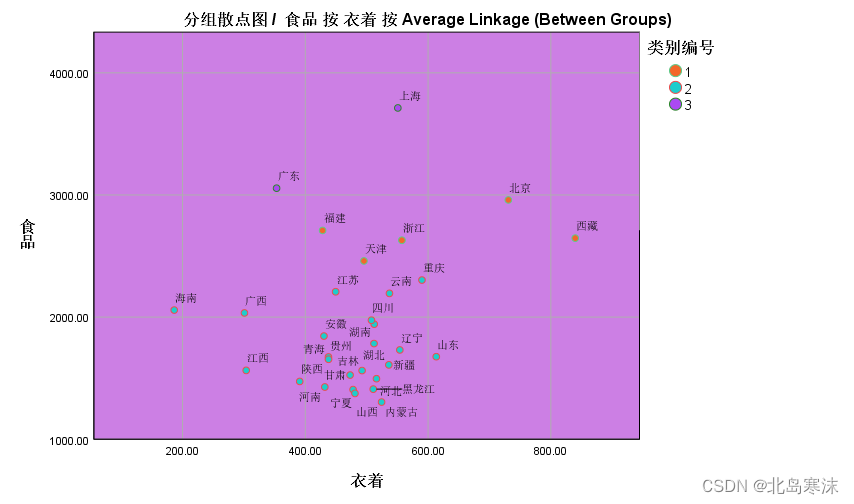
DBSCAN聚类算法

DBSCAN算法特点：

• 聚类前不需要指定簇的个数，生成的簇的个数与数据本身的特点有关。
• 可以在具有噪声的空间数据块中发现任意形状的簇，可以将密度足够大的相邻区域连接，能有效处理异常数据。

DBSCAN算法原理：要求聚类空间中的一定区域所包含对象的数目不小于某个给定的阈值。

DBSCAN算法中的三类数据点：

• 核心点：在半径内含有不少于指定阈值个数的其他点的点。
• 边界点：不是核心点，但是在核心点的邻域内；
• 噪音点：不是核心点且不是边界点的点。

DBSCAN算法优点：

• 可以处理任意形状和大小的簇；
• 可以在聚类的过程中发现异常点；
• 不需要指定簇的个数。

DBSCAN算法缺点：

• 对输入的参数非常敏感，确定参数困难；
• 当聚类的密度不均匀时聚类效果差；
• 当数据量大时，计算复杂度会非常高。