LeetCode 算法：二叉树的中序遍历 c++

news2025/1/17 14:05:09

原题链接🔗：二叉树的中序遍历
难度：简单⭐️

题目

给定一个二叉树的根节点 root ，返回它的中序遍历。

示例 1：
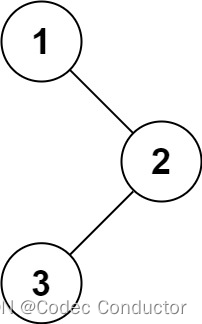
在这里插入图片描述

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

二叉树遍历

二叉树遍历是数据结构中的一个重要概念，它涉及到按照特定的顺序访问二叉树中的所有节点。二叉树的遍历主要有以下几种方式：

前序遍历（Pre-order Traversal）：
- 访问根节点。
- 遍历左子树（前序）。
- 遍历右子树（前序）。
中序遍历（In-order Traversal）：
- 遍历左子树（中序）。
- 访问根节点。
- 遍历右子树（中序）。
后序遍历（Post-order Traversal）：
- 遍历左子树（后序）。
- 遍历右子树（后序）。
- 访问根节点。
层序遍历（Level-order Traversal）：
- 使用队列实现，按照从上到下，从左到右的顺序访问每个节点。

每种遍历方式都有其特点和应用场景。下面是每种遍历方式的C++实现示例：

前序遍历

void preOrder(TreeNode* node) {
    if (node == nullptr) return;
    std::cout << node->val << " ";  // 访问根节点
    preOrder(node->left);            // 遍历左子树
    preOrder(node->right);           // 遍历右子树
}

中序遍历

void inOrder(TreeNode* node) {
    if (node == nullptr) return;
    inOrder(node->left);             // 遍历左子树
    std::cout << node->val << " ";  // 访问根节点
    inOrder(node->right);            // 遍历右子树
}

后序遍历

void postOrder(TreeNode* node) {
    if (node == nullptr) return;
    postOrder(node->left);           // 遍历左子树
    postOrder(node->right);          // 遍历右子树
    std::cout << node->val << " ";  // 访问根节点
}

层序遍历

void levelOrder(TreeNode* root) {
    if (root == nullptr) return;
    std::queue<TreeNode*> q;
    q.push(root);
    while (!q.empty()) {
        TreeNode* node = q.front();
        q.pop();
        std::cout << node->val << " ";
        if (node->left != nullptr) q.push(node->left);
        if (node->right != nullptr) q.push(node->right);
    }
}

在实际应用中，选择哪种遍历方式取决于你需要解决的问题。例如，如果你需要先访问根节点以决定后续操作，可能会选择前序遍历；如果你需要先访问所有子节点再访问根节点，可能会选择后序遍历；如果你需要按照树的层次顺序访问节点，可能会选择层序遍历。中序遍历通常用于二叉搜索树，因为它可以按照升序访问所有节点。

题解

递归法

解题思路：

二叉树的中序遍历解题思路主要基于深度优先搜索（DFS）策略。以下是中序遍历的一般步骤和思路：

理解中序遍历的顺序：中序遍历的特点是先访问左子树，然后是根节点，最后是右子树。

递归方法：

从根节点开始，递归地执行中序遍历。
对于每个节点，首先递归地遍历其左子节点。
访问当前节点（根节点）。
然后递归地遍历其右子节点。

使用栈实现非递归遍历：

使用一个栈来辅助实现非递归的中序遍历。
从根节点开始，将其压入栈中。
弹出栈顶元素，访问它的值，然后将其右子节点压入栈中。
如果弹出的节点有左子节点，将其左子节点压入栈中，重复上述步骤。
当栈为空时，遍历结束。

处理边界条件：确保在递归或非递归方法中处理空节点的情况。

代码实现：

定义一个二叉树节点结构，通常包含节点的值和指向左右子节点的指针。
实现中序遍历函数，可以是递归形式或使用栈的非递归形式。

测试：使用不同的二叉树结构来测试你的中序遍历算法，确保它可以正确地按照中序遍历的顺序访问所有节点。

优化：考虑算法的时间复杂度和空间复杂度。对于递归方法，注意递归深度可能影响性能；对于非递归方法，注意栈的使用可能会增加空间开销。

考虑特殊情况：例如，二叉树只有一个节点或没有节点，或者二叉树是一条链（所有节点只有左或只有右子节点）。

使用辅助数据结构：如果需要存储遍历结果，可以使用数组、列表或其他数据结构来收集遍历过程中访问的节点值。

复杂度：空间复杂度O(n)，时间复杂度O(n)。
c++ demo：

#include <iostream>
#include <vector>

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

void inorderTraversal(TreeNode* node) {
    if (node == nullptr) {
        return;
    }
    // 访问左子树
    inorderTraversal(node->left);
    // 访问根节点
    std::cout << node->val << " ";
    // 访问右子树
    inorderTraversal(node->right);
}

int main() {
    // 构建一个示例二叉树
    //       1
    //      / \
    //     2   3
    //     \
    //      4
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->right = new TreeNode(4);

    // 执行中序遍历
    std::cout << "Inorder traversal of the binary tree is: ";
    inorderTraversal(root);

    // 清理内存
    delete root->left->right;
    delete root->left;
    delete root->right;
    delete root;

    return 0;
}