1、背景介绍
前文已介绍对点云进行格网处理,可以计算平面点云面积、格网拓扑关系构建,相关博客如下:
(1)点云格网过程可视化(C++ PCL)-CSDN博客
(2)平面点云格网过程及可视化介绍(python)-CSDN博客
(3)详解基于格网法统计平面点云面积_点云格网法计算xy投影面积-CSDN博客
其实,点云格网化处理,还可以进行点云边缘检测,其思想类似数字图像处理,将点云进行格网化处理,类似生成一张图片,再依据非边缘格网特点识别边缘格网,以此达到边缘提取的目的。本次博客介绍利用构建的格网,实现边缘点检测,效果如下:
 |  |  |
2、原理介绍
位于边缘处的格网,其周边8个近邻格网均包含点,如下图所示,黄色格网,其周边的8个格网,均包含点集。对于位于边缘处格网,围绕其周围的8个格网,不全为空。因此,根据这一特征,可以探测边缘格网。
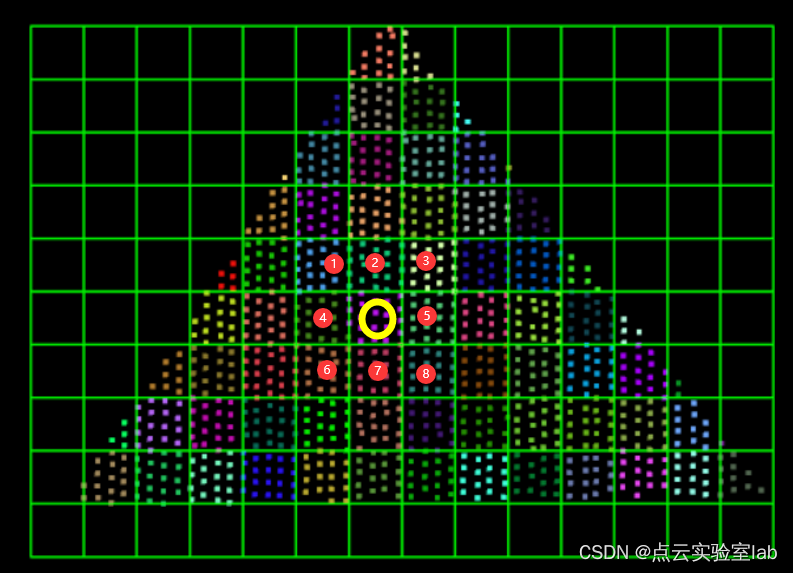
具体来说,对于一个包含点云数据的格网,根据该格网的行、列号(row、col),得到包含该格网的8个近邻格网的行、列号,分别如下:
(row-1,col-1)、(row-1,col)、(row-1,col+1)
(row,col-1)、 (row,col+1)
(row+1,col-1)、(row+1,col)、(row+1,col+1)
在获取8个近邻格网后,结合上述判断规则,获取边缘格网。
3、代码测试验证
本程序基于python编写,在pycharm上运行。下载代码链接如,下所包含的测试数据与代码如下图所示:
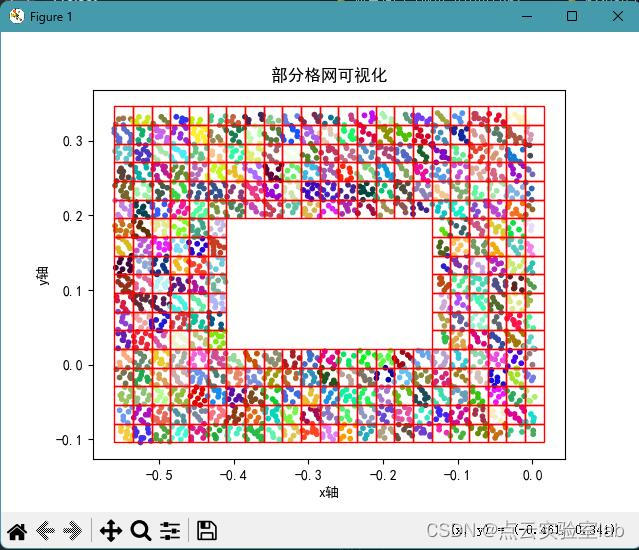
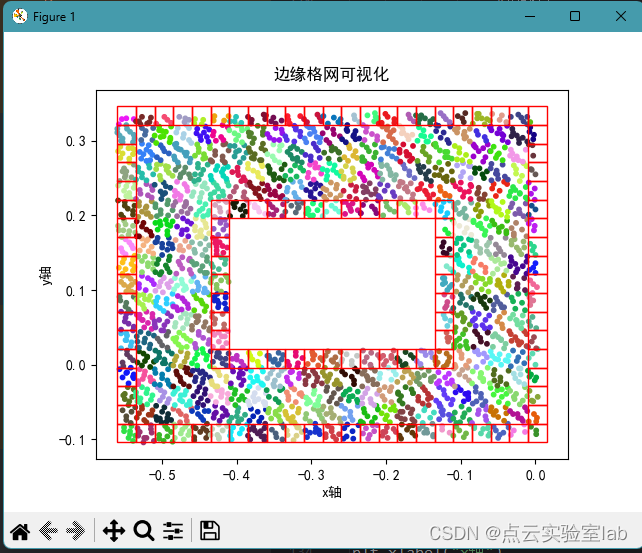
3.1 内部孔洞数据测试
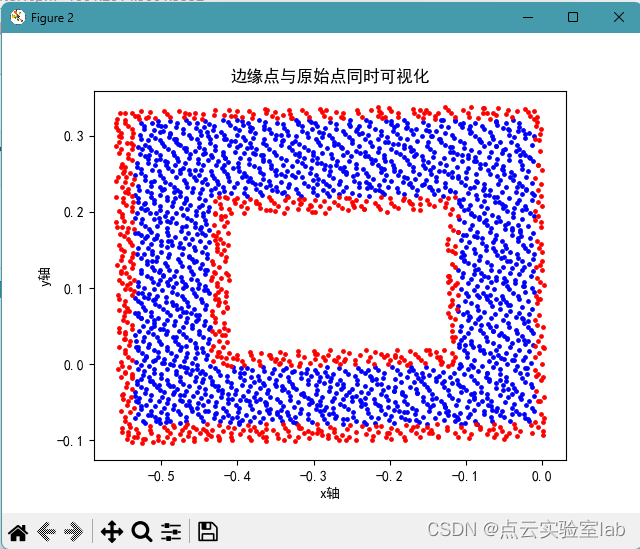
该点云分布的形状如下图所示,利用格网拓扑关系,得到的边缘格网分布如下图所示,可以发现边缘格网均分布在点云边界处,内部也存在边缘格网。随后提取的边缘点结果整体上比较理想。
 | 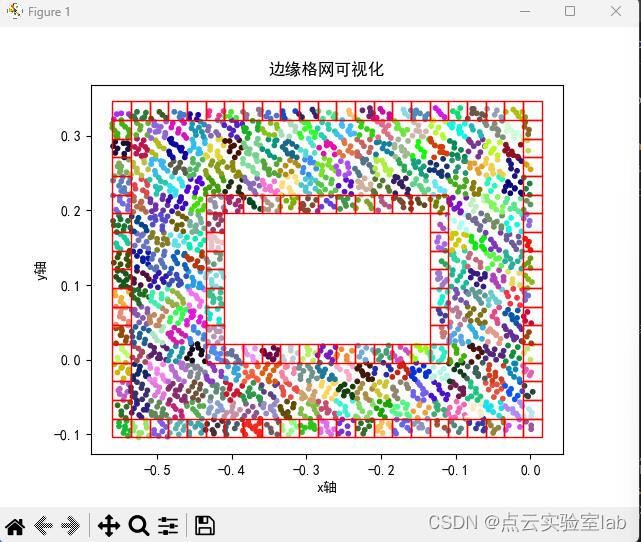 | 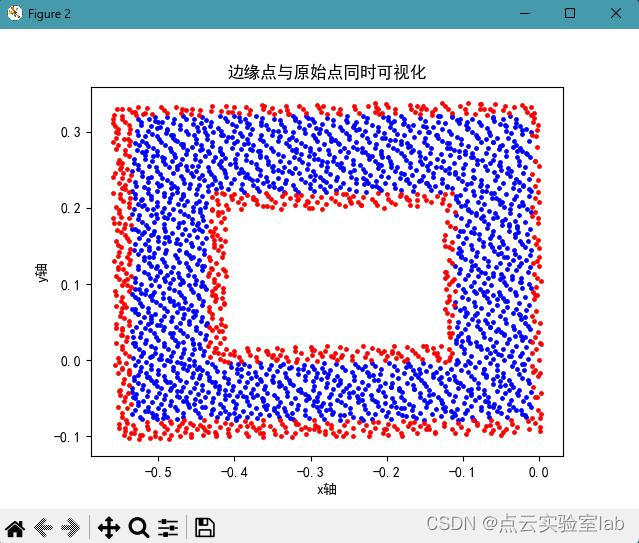 |
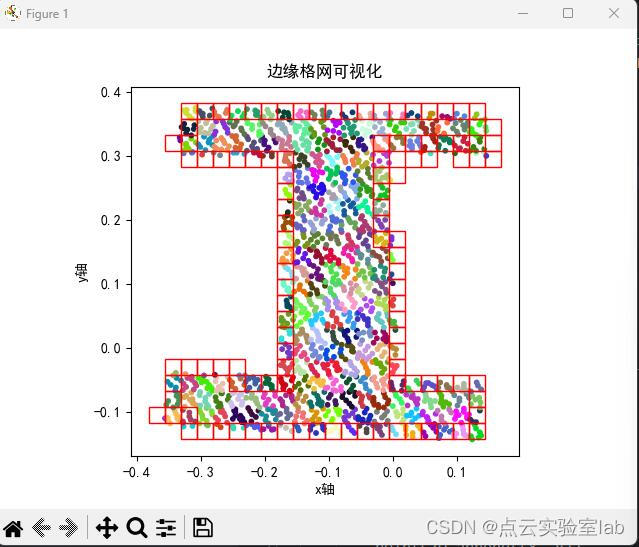
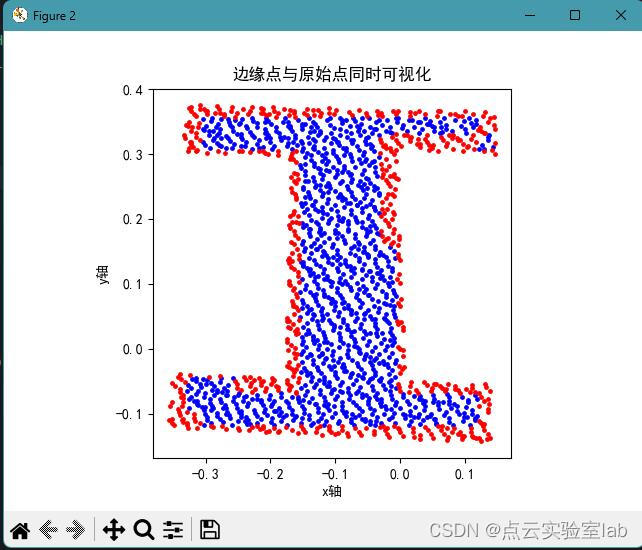
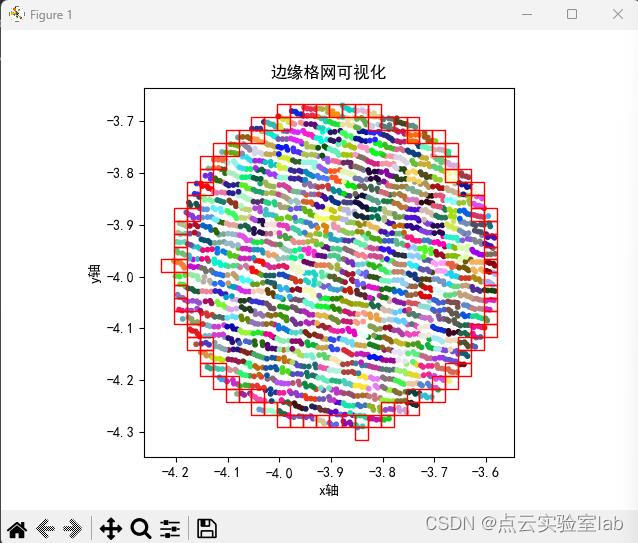
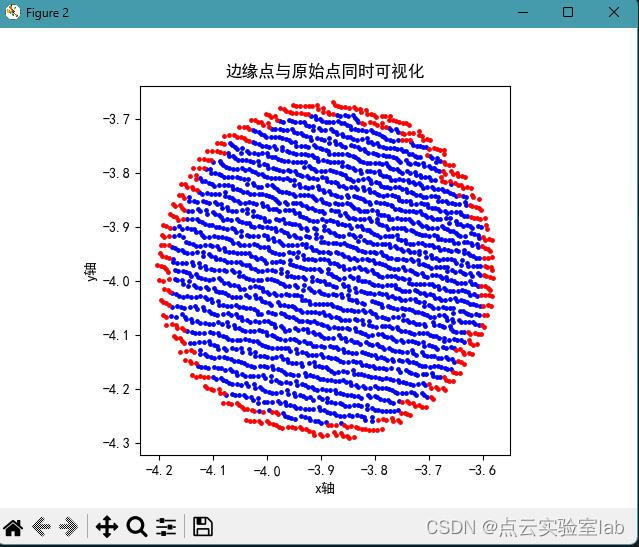
3.2 非孔洞点云提取
该点云分布的形状如下图所示,两簇点云均不包含内部孔洞,利用格网拓扑关系,得到的边缘格网分布如下图所示,可以发现边缘格网均分布在点云边界处。随后提取的边缘点结果整体上比较理想。
 |  |  |
 |  |  |
4、总结
该方法借鉴了数字图像提取边缘的思想,效率比较高,原理也比较简单。