前言

今天我们来学习与排序相关的面试题，首先我们先来学习冒泡排序，那什么是冒泡排序呢，它的关键在于数组中相邻元素进行比较，如果前一个小于后一个，它的位置可以不动，相反，则交换位置，依次两两进行相互比较，直到将数组中最大的元素放在最后的位置，每轮冒泡的结果就是将最大的元素放在数组的最后边，直到数组变为升序数组为止🎈🎈。

冒泡排序初步实现

我们知道冒泡排序需要两两比较，然后可能会交换顺序，所以我们需要自己定义一个静态方法swap()实现交换顺序的功能，同样再写一个bubble()方法实现冒泡排序，最后在主方法中调用，每轮冒泡排序需要比较数组长度-1次，一共需要进行数组长度-1次冒泡排序，所以bubble()方法里边采用的是双重循环来实现的，下面是我们冒泡排序的初步代码👇👇。

public class BubbleSort {
    public static void main(String[] args) {
        int []a = {5,9,7,4,1,3,2,8};
        bubble(a);
    }

    public static void bubble(int []a){

        for (int j =0;j<a.length-1;j++) {
            //一轮冒泡
            for (int i = 0; i < a.length-1 ; i++) {
               if(a[i]>a[i+1]){
                   swap(a,i,i+1);
               }
            }
            System.out.println("第"+j+"轮冒泡"+Arrays.toString(a));
        }

    }

    public static void swap(int[]a,int i, int j){
        int t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
}

在这里插入图片描述

我们来分析一下代码，在冒泡排序中，我们每一次都是将数组最大的元素放在数组最后面，所以在进行下一轮冒泡排序的时候，数组最后边的元素已经是最大的了，所以不用再进行比较，所以我们接下来要对上边的代码进行优化💪💪。

冒泡排序_优化_减少比较次数

接下来我们对冒泡排序的比较次数进行优化，上述代码中，第一轮冒泡排序需要比较七次，结果是将数组最大的元素9放在了数组最后的索引位置，第二轮冒泡排序时，就不用再与9进行比较，所以需要比较六次，以此类推，每一轮冒泡排序都会减少一次比较次数，我们总结出规律，将内层循环的次数改为i<a.length-1-j就可以减少比较次数了，结果相同，但是效率会更高🎉🎉。

public class BubbleSort {
    public static void main(String[] args) {
        int []a = {5,9,7,4,1,3,2,8};
        bubble(a);
    }

    public static void bubble(int []a){

        for (int j =0;j<a.length-1;j++) {
            //一轮冒泡
            for (int i = 0; i < a.length-1-j ; i++) {
               if(a[i]>a[i+1]){
                   swap(a,i,i+1);
               }
            }
            System.out.println("第"+j+"轮冒泡"+Arrays.toString(a));
        }

    }

    public static void swap(int[]a,int i, int j){
        int t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
}

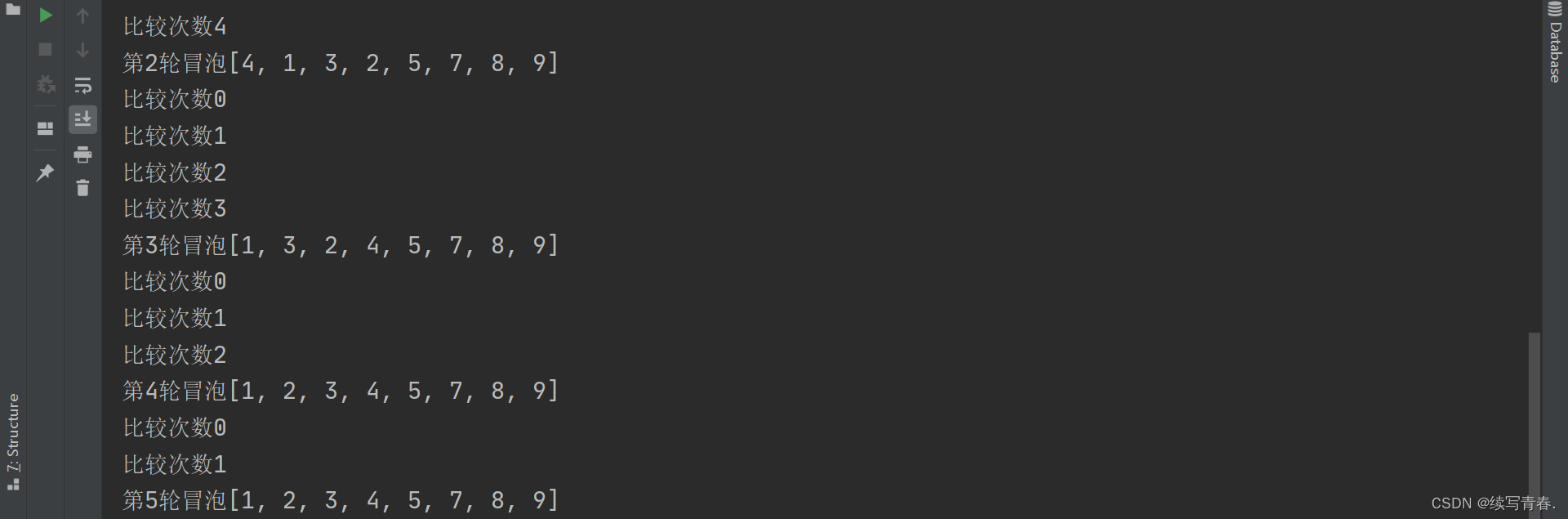
在这里插入图片描述

我们分析运行结果，第四轮冒泡排序完成后，其实数组已经是一个升序数组了，不用再进行第五轮和第六轮冒泡排序了，所以我们还要对代码进行进一步的优化💪💪。

冒泡排序_优化_减少冒泡次数

那怎么去进行优化呢，也就是怎么去判断你这个数组是有序的，什么时候能得到这个数组已经有序，不用冒泡了呢，我们可以这么来想，如果它某一轮冒泡排序，相邻元素两两进行比较，没有发生过一次交换，那是不是就证明数组已经有序了，那我们就可以以数组有没有交换作为判断依据，在代码中，我们可以在每次冒泡排序前，设置一个boolean swapped=false,表示还没有交换，然后在if()判断里边设置swapped=true表示如果发生了交换，就将swapped的值设置为true,最后在每次冒泡排序完成后·判断swapped的值是否为false·,如果为false,就break跳出外层循环，结束冒泡排序👇👇。

public class BubbleSort {
    public static void main(String[] args) {
        int []a = {5,9,7,4,1,3,2,8};
        bubble(a);
    }

    public static void bubble(int []a){

        for (int j =0;j<a.length-1;j++) {
            //一轮冒泡
            boolean swapped = false;
            for (int i = 0; i < a.length-1-j ; i++) {
                System.out.println("比较次数"+i);
               if(a[i]>a[i+1]){
                   swap(a,i,i+1);
                   swapped = true;
               }
            }
            System.out.println("第"+j+"轮冒泡"+Arrays.toString(a));
            if(!swapped){
               break;
            }
        }

    }

    public static void swap(int[]a,int i, int j){
        int t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
}

在这里插入图片描述

冒泡排序_优化_进一步优化比较次数

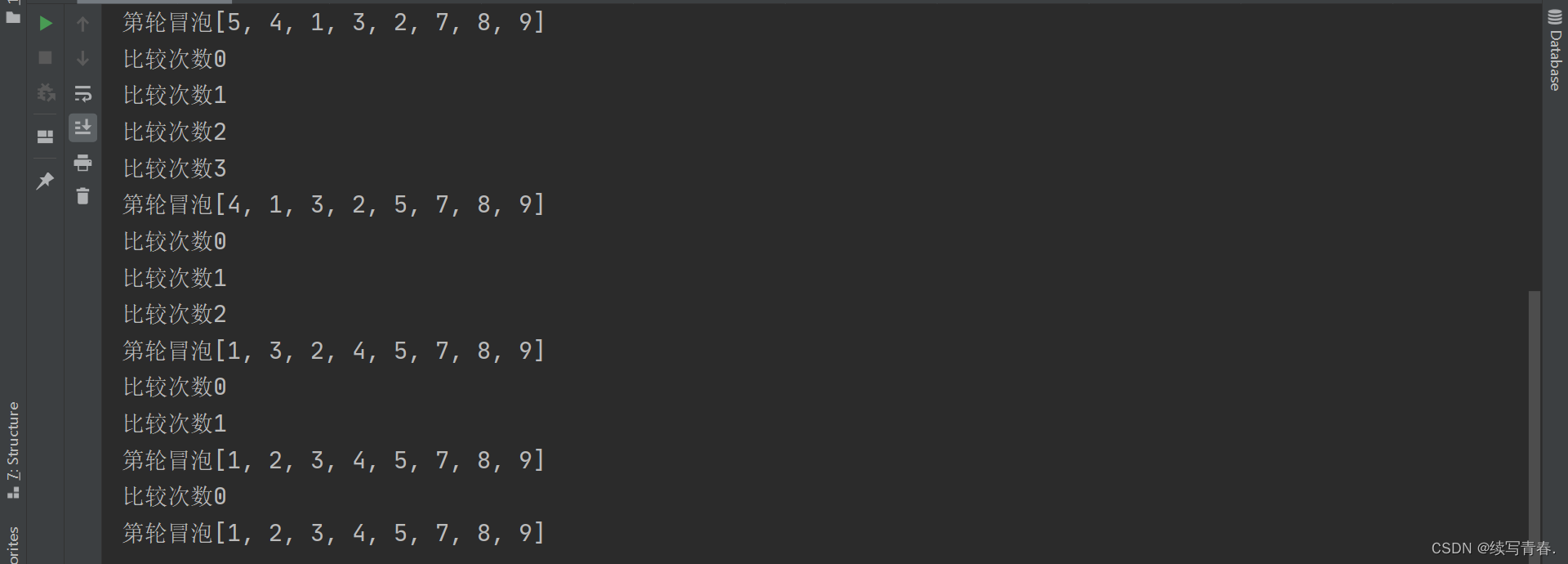
虽然前边已经对冒泡排序进行了优化，但是还有一种比较特殊的情况，比如现在有一个无序数组：{5,2,7,4,1,3,8,9},在经历第一轮冒泡排序经历七次比较后变为{2,5,4,1,3,7,8,9}，这个时候能确定的最大元素是9，接下来第二轮冒泡排序时，我们会发现仍然是需要比较六次，但是我们自己知道其实第二轮不用再比较六次，因为第一轮8跟9，5跟7都已经比较过了，所以下一轮冒泡排序的时候，没有必要再进行比较，所以我们要进一步优化✍️✍️。

那怎么去优化呢，我们只需要在每次冒泡排序完记录最后一次交换发生的位置，来当做下一轮冒泡排序的比较次数🎉🎉。

public class BubbleSort {
    public static void main(String[] args) {
        int []a = {5,9,7,4,1,3,2,8};
        bubble_v2(a);
    }

    public static void bubble_v2(int[]a){
        int n = a.length-1;
        while (true) {
            int last=0;//表示最后一次交换索引的位置
            for (int i = 0; i < n; i++) {
                System.out.println("比较次数"+i);
                if(a[i]>a[i+1]){
                    swap(a,i,i+1);
                    last = i;
                }
            }
                n = last;
            System.out.println("第轮冒泡"+Arrays.toString(a));
            if(n==0){
                break;
            }
        }
    }
     public static void swap(int[]a,int i, int j){
        int t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
}