稀疏表示方法是一种利用最少原子在过完备字典上表示或逼近信号的方法,该方法具有信号表示的高分辨率、稀疏性、强抗干扰能力和自适应性等优点。稀疏表示聚焦于设计合适的稀疏表示字典和挖掘有用的稀疏先验信息,其核心思想是将故障特征信息近似表示为字典中少量原子的组合。由于旋转机械的高转速导致故障波形混叠变异,同时复杂的结构导致故障波形受到时变噪声及谐波的干扰,因此,旋转机械信号是极其复杂的。稀疏表示能够适用于任意复杂信号的描述,该方法利用冗余和超完备字典进行原子分解,具有高度的灵活性和适应性。
当滚动轴承发生局部故障时,会产生具有稀疏性和准周期性的故障信号,这是局部故障的关键特征,但是噪声干扰则不具备稀疏性和准周期性,因此可以通过稀疏表示方法准确地用少数原子表示轴承故障信号。
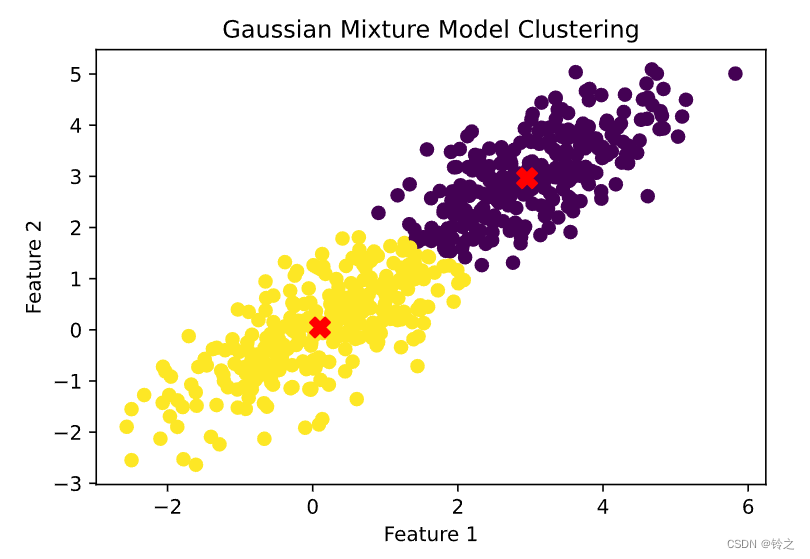
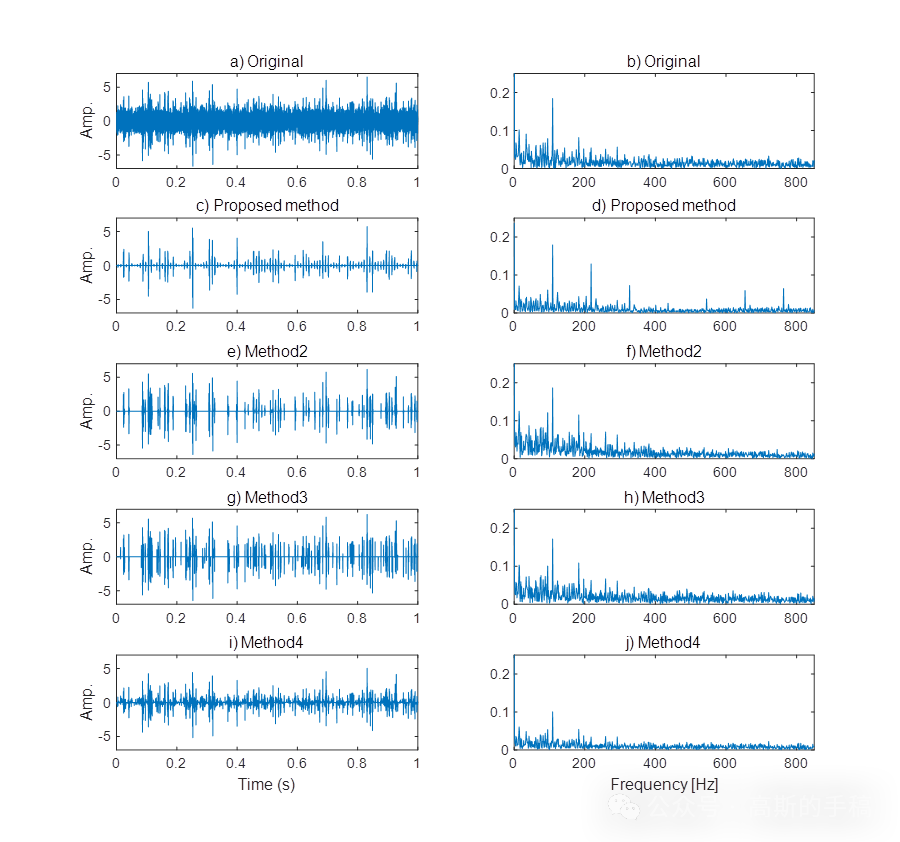
鉴于此,采用一种与稀疏表示方法类似的稀疏学习方法对旋转机械进行故障诊断,即稀疏贝叶斯学习故障诊断框架,运行环境为MATLAB R2018A,运行结果如下:
narginchk(2,10)
Sig = squeeze(Sig);
if size(Sig,1) == 2
Sig = Sig';
end
p = inputParser;
Chk1 = @(x) isnumeric(x) && ismatrix(x) && (min(size(x)) ==2) && numel(x)>20;
addRequired(p,'Sig',Chk1);
addRequired(p,'Mobj',@(x) isstruct(x));
addParameter(p,'Scales',3,@(x) isnumeric(x) && (length(x)==1) && (x>1));
addParameter(p,'RadNew',0,@(x) ismember(x,0:4) && ...
any(validatestring(func2str(Mobj.Func),{'XSampEn';'XApEn'})));
addParameter(p,'Refined',false,@(x) islogical(x) && ...
any(validatestring(func2str(Mobj.Func),{'XSampEn'})));
addParameter(p,'Plotx',false,@(x) islogical(x));
parse(p,Sig, Mobj, varargin{:})
MSx = zeros(1,p.Results.Scales);
RadNew = p.Results.RadNew;
Fields = fieldnames(Mobj);
Y = struct2cell(Mobj);
C = [Fields(2:end),Y(2:end)].';
完整代码可通过知乎学术咨询获得:
https://www.zhihu.com/consult/people/792359672131756032?isMe=1擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。