- 数据探索
波士顿房价数据集:卡内基梅隆大学收集,StatLib库,1978年,涵盖了麻省波士顿的506个不同郊区的房屋数据。
一共含有506条数据。每条数据14个字段,包含13个属性,和一个房价的平均值。
数据读取方法:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
names =['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT','MEDV']
data=pd.read_csv('housing.csv', names=names, delim_whitespace=True)
data1=data.head(10)- 请绘制散点图探索波士顿房价数据集中犯罪率(CRIM)和房价中位数(MEDV)之间的相关性。
# 创建散点图
sns.scatterplot(x=data1['CRIM'], y=data1['ZN'])
# 添加数据标签
for i in range(len(data1['CRIM'])):
plt.text(data1['CRIM'][i], data1['ZN'][i], str(i), fontsize=8, color='black')
# 添加标题
plt.title('Correlation between CRIM and ZN')
# 显示图形
plt.show() 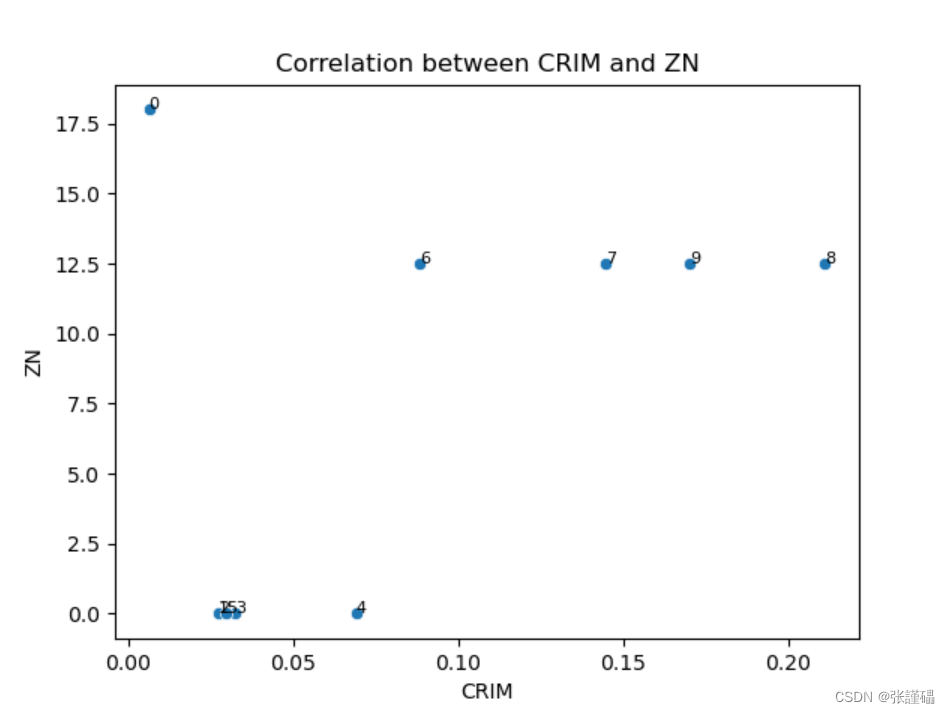
- 请使用波士顿房价数据集中房价中位数(MEDV)来绘制箱线图。
# 创建箱线图
sns.boxplot(data['CRIM'])
# 添加数据标签
# for i in range(len(data['CRIM'])):
# plt.text(1, data['CRIM'][i], data['CRIM'][i], horizontalalignment='center', verticalalignment='bottom')
plt.title('Boxplot of CRIM')
plt.show() 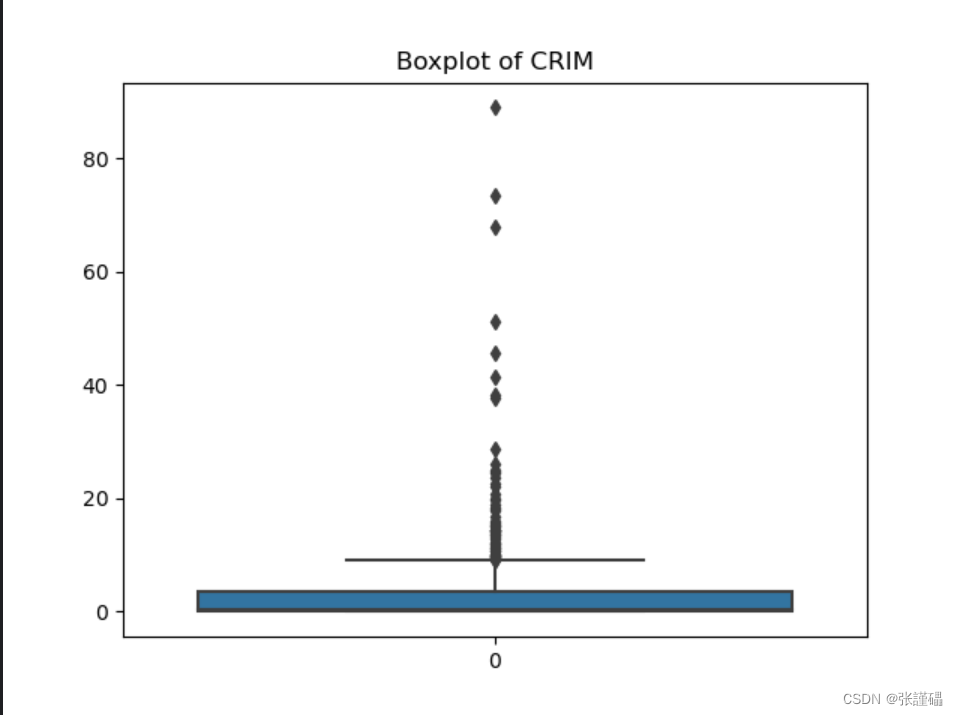
- 请使用暗点图矩阵探索波士顿房价数据集。
sns.pairplot(data)
plt.show()
print(data['CRIM'].corr(data['MEDV'],method='pearson'))
print(data['CRIM'].corr(data['MEDV'],method='spearman'))
print(data['CRIM'].corr(data['MEDV'],method='kendall')) 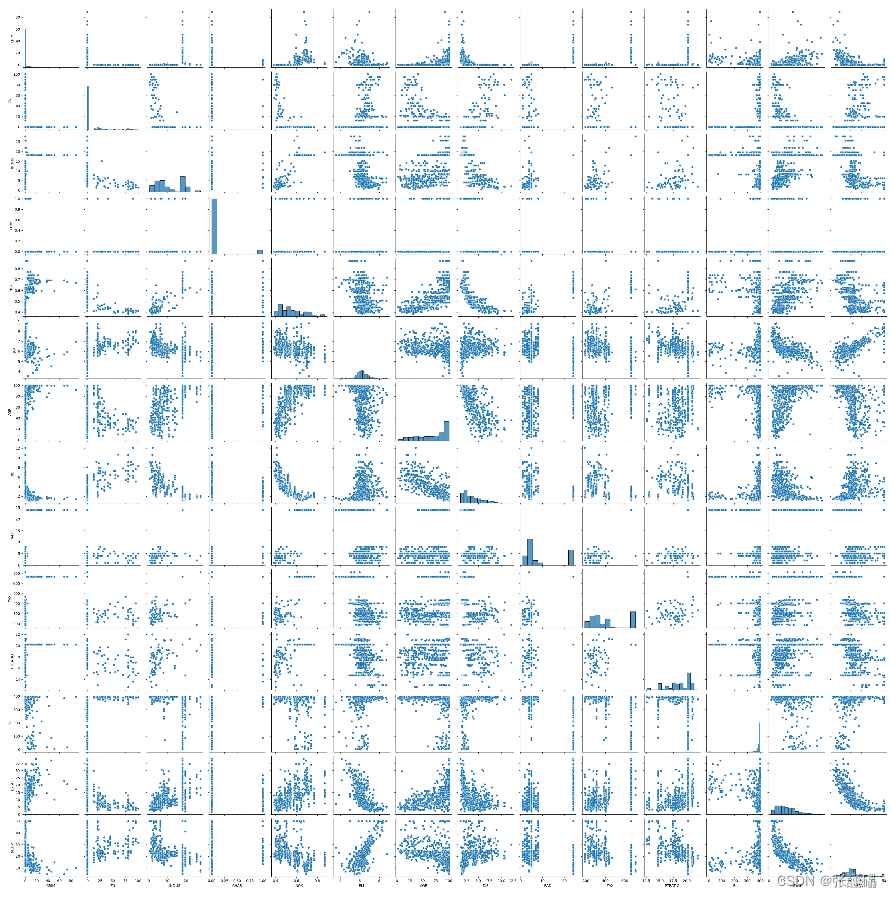
- 请分别使用皮尔逊(pearson)、斯皮尔曼(spearman)、肯德尔(kendall)相关系数对犯罪率(CRIM)和房价中位数(MEDV)之间的相关性进行度量。
print(data['CRIM'].corr(data['MEDV'],method='pearson'))
print(data['CRIM'].corr(data['MEDV'],method='spearman'))
print(data['CRIM'].corr(data['MEDV'],method='kendall'))

相关系数计算方法:
- 请绘制波士顿房价数据集中各变量之间相关系数的热力图。
需提前安装seaborn库:pip install seaborn
plt.figure(figsize=(12, 10))
sns.heatmap(data.corr(),annot=True,cmap='Blues_r')
plt.show() 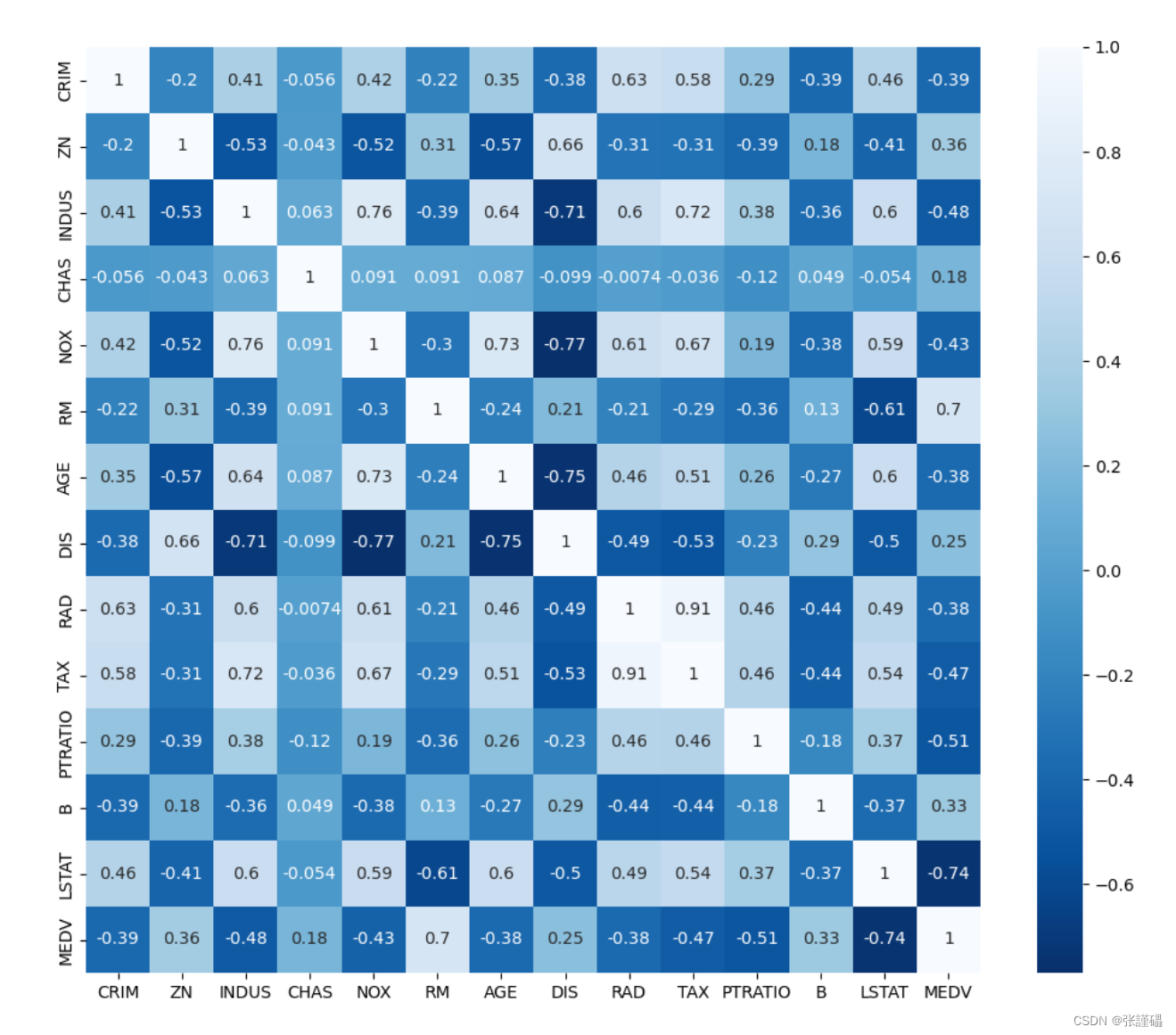
- 数据预处理
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | y |
| 1 | 22.08 | 11.46 | 2 | 4 | 4 | 1.585 | 0 | 0 | 0 | 1 | 2 | 100 | 1213 | 0 |
| 0 | 22.67 | 7 | 2 | 8 | 4 | 0.165 | 0 | 0 | 0 | 0 | 2 | 160 | 1 | 0 |
| 0 | 29.58 | 1.75 | 1 | 4 | 4 | 1.25 | 0 | 0 | 0 | 1 | 2 | 280 | 1 | 0 |
| 0 | 21.67 | 1 | 5 | 3 | 0 | 1 | 1 | 11 | 1 | 2 | 0 | 1 | 1 | |
| 1 | 20.17 | 8.17 | 2 | 6 | 4 | 1.96 | 1 | 1 | 14 | 0 | 2 | 60 | 159 | 1 |
| 0 | 0.585 | 2 | 8 | 8 | 1 | 1 | 2 | 0 | 2 | 1 | 1 | |||
| 1 | 17.42 | 6.5 | 2 | 3 | 4 | 0.125 | 0 | 0 | 0 | 0 | 2 | 60 | 101 | 0 |
| 0 | 58.67 | 4.46 | 2 | 11 | 8 | 3.04 | 1 | 1 | 6 | 0 | 2 | 43 | 561 | 1 |
| 1 | 27.83 | 1 | 1 | 2 | 8 | 3 | 0 | 0 | 0 | 0 | 2 | 176 | 538 | 0 |
| 0 | 55.75 | 7.08 | 2 | 4 | 8 | 6.75 | 1 | 1 | 3 | 1 | 2 | 100 | 51 | 0 |
| 1 | 33.5 | 1.75 | 2 | 14 | 8 | 1 | 1 | 4 | 1 | 2 | 253 | 858 | 1 | |
| 1 | 41.42 | 5 | 2 | 11 | 8 | 5 | 1 | 1 | 6 | 1 | 2 | 470 | 1 | 1 |
| 1 | 20.67 | 1.25 | 1 | 8 | 8 | 1.375 | 1 | 1 | 3 | 1 | 2 | 140 | 0 | |
| 34.92 | 5 | 2 | 14 | 8 | 7.5 | 1 | 1 | 6 | 1 | 2 | 0 | 1001 | 1 | |
| 1 | 2.71 | 2 | 8 | 4 | 2.415 | 0 | 0 | 1 | 2 | 320 | 1 | 0 | ||
| 1 | 48.08 | 6.04 | 2 | 4 | 4 | 0 | 0 | 0 | 0 | 2 | 0 | 2691 | 1 | |
| 1 | 29.58 | 4.5 | 2 | 9 | 4 | 7.5 | 1 | 1 | 2 | 1 | 2 | 330 | 1 | 1 |
| 0 | 18.92 | 9 | 2 | 6 | 4 | 0.75 | 1 | 1 | 2 | 0 | 2 | 88 | 592 | 1 |
| 1 | 20 | 1.25 | 1 | 4 | 4 | 0.125 | 0 | 0 | 0 | 0 | 2 | 140 | 5 | 0 |
| 0 | 22.42 | 5.665 | 2 | 11 | 4 | 2.585 | 1 | 7 | 0 | 2 | 129 | 3258 | 1 | |
| 0 | 28.17 | 0.585 | 2 | 6 | 4 | 0.04 | 0 | 0 | 0 | 2 | 1005 | 0 | ||
| 0 | 19.17 | 0.585 | 1 | 6 | 4 | 0.585 | 1 | 0 | 0 | 1 | 2 | 160 | 1 | 0 |
| 1 | 41.17 | 1.335 | 2 | 2 | 4 | 0.165 | 0 | 0 | 0 | 0 | 2 | 168 | 1 | 0 |
| 1 | 41.58 | 1.75 | 2 | 4 | 4 | 0.21 | 1 | 0 | 0 | 2 | 160 | 1 | 0 | |
| 19.5 | 2 | 6 | 4 | 0.79 | 0 | 0 | 0 | 0 | 2 | 80 | 351 | 0 | ||
| 1 | 32.75 | 1.5 | 2 | 13 | 8 | 5.5 | 1 | 1 | 3 | 1 | 2 | 0 | 1 | 1 |
| 1 | 22.5 | 0.125 | 1 | 4 | 4 | 0.125 | 0 | 0 | 0 | 0 | 2 | 200 | 71 | 0 |
| 1 | 33.17 | 3.04 | 1 | 8 | 8 | 2.04 | 1 | 1 | 1 | 1 | 2 | 180 | 18028 | 1 |
| 0 | 30.67 | 12 | 2 | 8 | 4 | 2 | 1 | 1 | 1 | 0 | 2 | 220 | 20 | 1 |
| 1 | 23.08 | 2.5 | 2 | 8 | 4 | 1.085 | 1 | 1 | 11 | 1 | 2 | 60 | 2185 | 1 |
| 1 | 27 | 0.75 | 2 | 8 | 8 | 1 | 1 | 3 | 1 | 2 | 312 | 151 | 1 | |
| 0 | 20.42 | 10.5 | 1 | 14 | 8 | 0 | 0 | 0 | 0 | 1 | 2 | 154 | 33 | 0 |
| 1 | 52.33 | 1.375 | 1 | 8 | 8 | 9.46 | 1 | 0 | 1 | 2 | 200 | 101 | 0 | |
| 1 | 23.08 | 11.5 | 2 | 9 | 8 | 2.125 | 1 | 1 | 11 | 1 | 2 | 290 | 285 | 1 |
| 1 | 42.83 | 1.25 | 2 | 7 | 4 | 13.875 | 0 | 1 | 1 | 1 | 2 | 352 | 113 | 0 |
| 1 | 74.83 | 19 | 1 | 1 | 1 | 0.04 | 0 | 1 | 2 | 0 | 2 | 0 | 352 | 0 |
| 1 | 25 | 2 | 6 | 4 | 3 | 1 | 0 | 0 | 1 | 20 | 1 | 1 | ||
| 1 | 39.58 | 13.915 | 2 | 9 | 4 | 8.625 | 1 | 1 | 6 | 1 | 2 | 70 | 1 | 1 |
| 0 | 47.75 | 8 | 2 | 8 | 4 | 7.875 | 1 | 1 | 6 | 1 | 2 | 0 | 1261 | 1 |
| 0 | 47.42 | 3 | 2 | 14 | 4 | 13.875 | 1 | 1 | 2 | 1 | 2 | 519 | 1705 | 1 |
| 1 | 23.17 | 0 | 2 | 13 | 4 | 0.085 | 1 | 0 | 0 | 2 | 0 | 1 | 1 | |
| 1 | 22.58 | 1.5 | 1 | 6 | 4 | 0.54 | 0 | 0 | 0 | 1 | 2 | 120 | 68 | 0 |
| 1 | 26.75 | 1.125 | 2 | 14 | 8 | 1.25 | 1 | 0 | 0 | 0 | 2 | 0 | 5299 | 1 |
| 1 | 63.33 | 0.54 | 2 | 8 | 4 | 0.585 | 1 | 1 | 3 | 1 | 2 | 180 | 1 | 0 |
| 1 | 23.75 | 0.415 | 1 | 8 | 4 | 0.04 | 0 | 1 | 2 | 0 | 2 | 128 | 7 | 0 |
| 0 | 20.75 | 2 | 11 | 4 | 0.71 | 1 | 1 | 2 | 1 | 2 | 49 | 1 | 1 | |
| 0 | 24.5 | 1.75 | 1 | 8 | 4 | 0.165 | 0 | 0 | 0 | 0 | 2 | 132 | 1 | 0 |
| 1 | 16.17 | 0.04 | 2 | 8 | 4 | 0.04 | 0 | 0 | 0 | 0 | 2 | 0 | 1 | 1 |
| 0 | 29.5 | 2 | 1 | 10 | 8 | 2 | 0 | 0 | 0 | 0 | 2 | 256 | 18 | 0 |
| 0 | 52.83 | 15 | 2 | 8 | 4 | 5.5 | 1 | 1 | 14 | 0 | 2 | 0 | 2201 | 1 |
| 1 | 32.33 | 3.5 | 2 | 4 | 4 | 0.5 | 0 | 0 | 0 | 1 | 2 | 232 | 1 | 0 |
| 1 | 21.08 | 4.125 | 1 | 3 | 8 | 0.04 | 0 | 0 | 0 | 2 | 140 | 101 | 0 | |
| 1 | 28.17 | 0.125 | 1 | 4 | 4 | 0.085 | 0 | 0 | 0 | 0 | 2 | 216 | 2101 | 0 |
| 1 | 19 | 1.75 | 1 | 8 | 4 | 2.335 | 0 | 0 | 0 | 1 | 2 | 112 | 7 | 0 |
| 1 | 27.58 | 3.25 | 11 | 8 | 5.085 | 0 | 1 | 2 | 1 | 2 | 2 | 0 | ||
| 1 | 27.83 | 1.5 | 2 | 9 | 4 | 2 | 1 | 1 | 11 | 1 | 2 | 434 | 36 | 1 |
| 1 | 6.5 | 2 | 6 | 5 | 3.5 | 1 | 1 | 1 | 0 | 2 | 0 | 501 | 1 | |
| 0 | 37.33 | 2.5 | 2 | 3 | 8 | 0.21 | 0 | 0 | 0 | 0 | 2 | 260 | 0 | |
| 1 | 42.5 | 4.915 | 1 | 9 | 4 | 3.165 | 1 | 0 | 1 | 2 | 52 | 1443 | 1 | |
| 1 | 56.75 | 12.25 | 2 | 7 | 4 | 1.25 | 1 | 1 | 4 | 1 | 2 | 200 | 1 | 1 |
| 1 | 43.17 | 5 | 2 | 3 | 5 | 2.25 | 0 | 0 | 0 | 1 | 2 | 141 | 1 | 0 |
| 0 | 23.75 | 0.71 | 2 | 9 | 4 | 0.25 | 0 | 1 | 1 | 1 | 2 | 240 | 5 | 0 |
| 1 | 18.5 | 2 | 2 | 3 | 4 | 1.5 | 1 | 1 | 2 | 0 | 2 | 120 | 301 | 1 |
| 0 | 40.83 | 3.5 | 2 | 3 | 5 | 0.5 | 0 | 0 | 0 | 0 | 1 | 1160 | 1 | 0 |
| 0 | 24.5 | 0.5 | 2 | 11 | 8 | 1.5 | 1 | 0 | 0 | 0 | 2 | 280 | 825 | 1 |
- 读取“银行贷款审批数据.xlsx”表,自变量为x1-x14,决策变量为y(1-同意贷款,0-不同意贷款),自变量中有连续变量(x2,x3,x5,x6,x7,x10,x13,x14)和离散变量(x1,x4,x8,x9,x11,x12),请对连续变量中的缺失值用均值策略填充,对离散变量中的缺失值用最频繁值策略填充。
import pandas as pd
# 读取Excel文件
df = pd.read_excel("银行贷款审批数据.xlsx")
# 定义连续变量和离散变量列表
continuous_vars = ['x2', 'x3', 'x5', 'x6', 'x7', 'x10', 'x13', 'x14']
discrete_vars = ['x1', 'x4', 'x8', 'x9', 'x11', 'x12']
# 使用均值填充连续变量的缺失值
for var in continuous_vars:
df[var].fillna(df[var].mean(), inplace=True)
# 使用最频繁值填充离散变量的缺失值
for var in discrete_vars:
most_frequent_value = df[var].mode()[0]
df[var].fillna(most_frequent_value, inplace=True)
# 检查是否还有缺失值
missing_values = df.isnull().sum().sum()
if missing_values == 0:
print("所有缺失值已填充。")
else:
print("仍有缺失值未填充。")
# 输出填充后的数据框的前几行
print(df.head())
# 保存填充后的数据框到Excel文件
df.to_excel("填充后的银行贷款审批数据.xlsx", index=False) 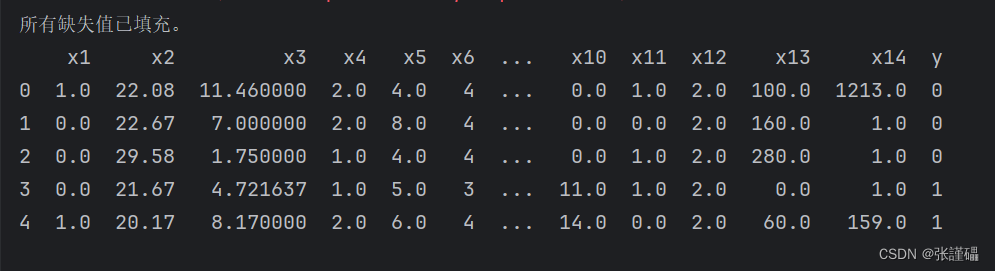
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | y |
| 1 | 22.08 | 11.46 | 2 | 4 | 4 | 1.585 | 0 | 0 | 0 | 1 | 2 | 100 | 1213 | 0 |
| 0 | 22.67 | 7 | 2 | 8 | 4 | 0.165 | 0 | 0 | 0 | 0 | 2 | 160 | 1 | 0 |
| 0 | 29.58 | 1.75 | 1 | 4 | 4 | 1.25 | 0 | 0 | 0 | 1 | 2 | 280 | 1 | 0 |
| 0 | 21.67 | 4.721637298 | 1 | 5 | 3 | 0 | 1 | 1 | 11 | 1 | 2 | 0 | 1 | 1 |
| 1 | 20.17 | 8.17 | 2 | 6 | 4 | 1.96 | 1 | 1 | 14 | 0 | 2 | 60 | 159 | 1 |
| 0 | 31.59438053 | 0.585 | 2 | 8 | 8 | 2.229175258 | 1 | 1 | 2 | 0 | 2 | 183.7609971 | 1 | 1 |
| 1 | 17.42 | 6.5 | 2 | 3 | 4 | 0.125 | 0 | 0 | 0 | 0 | 2 | 60 | 101 | 0 |
| 0 | 58.67 | 4.46 | 2 | 11 | 8 | 3.04 | 1 | 1 | 6 | 0 | 2 | 43 | 561 | 1 |
| 1 | 27.83 | 1 | 1 | 2 | 8 | 3 | 0 | 0 | 0 | 0 | 2 | 176 | 538 | 0 |
| 0 | 55.75 | 7.08 | 2 | 4 | 8 | 6.75 | 1 | 1 | 3 | 1 | 2 | 100 | 51 | 0 |
| 1 | 33.5 | 1.75 | 2 | 14 | 8 | 2.229175258 | 1 | 1 | 4 | 1 | 2 | 253 | 858 | 1 |
| 1 | 41.42 | 5 | 2 | 11 | 8 | 5 | 1 | 1 | 6 | 1 | 2 | 470 | 1 | 1 |
| 1 | 20.67 | 1.25 | 1 | 8 | 8 | 1.375 | 1 | 1 | 3 | 1 | 2 | 140 | 1023.653061 | 0 |
| 1 | 34.92 | 5 | 2 | 14 | 8 | 7.5 | 1 | 1 | 6 | 1 | 2 | 0 | 1001 | 1 |
| 1 | 31.59438053 | 2.71 | 2 | 8 | 4 | 2.415 | 0 | 0 | 2.424597365 | 1 | 2 | 320 | 1 | 0 |
| 1 | 48.08 | 6.04 | 2 | 4 | 4 | 2.229175258 | 0 | 0 | 0 | 0 | 2 | 0 | 2691 | 1 |
| 1 | 29.58 | 4.5 | 2 | 9 | 4 | 7.5 | 1 | 1 | 2 | 1 | 2 | 330 | 1 | 1 |
| 0 | 18.92 | 9 | 2 | 6 | 4 | 0.75 | 1 | 1 | 2 | 0 | 2 | 88 | 592 | 1 |
| 1 | 20 | 1.25 | 1 | 4 | 4 | 0.125 | 0 | 0 | 0 | 0 | 2 | 140 | 5 | 0 |
| 0 | 22.42 | 5.665 | 2 | 11 | 4 | 2.585 | 1 | 0 | 7 | 0 | 2 | 129 | 3258 | 1 |
| 0 | 28.17 | 0.585 | 2 | 6 | 4 | 0.04 | 1 | 0 | 0 | 0 | 2 | 183.7609971 | 1005 | 0 |
| 0 | 19.17 | 0.585 | 1 | 6 | 4 | 0.585 | 1 | 0 | 0 | 1 | 2 | 160 | 1 | 0 |
| 1 | 41.17 | 1.335 | 2 | 2 | 4 | 0.165 | 0 | 0 | 0 | 0 | 2 | 168 | 1 | 0 |
| 1 | 41.58 | 1.75 | 2 | 4 | 4 | 0.21 | 1 | 0 | 2.424597365 | 0 | 2 | 160 | 1 | 0 |
| 1 | 19.5 | 4.721637298 | 2 | 6 | 4 | 0.79 | 0 | 0 | 0 | 0 | 2 | 80 | 351 | 0 |
| 1 | 32.75 | 1.5 | 2 | 13 | 8 | 5.5 | 1 | 1 | 3 | 1 | 2 | 0 | 1 | 1 |
| 1 | 22.5 | 0.125 | 1 | 4 | 4 | 0.125 | 0 | 0 | 0 | 0 | 2 | 200 | 71 | 0 |
| 1 | 33.17 | 3.04 | 1 | 8 | 8 | 2.04 | 1 | 1 | 1 | 1 | 2 | 180 | 18028 | 1 |
| 0 | 30.67 | 12 | 2 | 8 | 4 | 2 | 1 | 1 | 1 | 0 | 2 | 220 | 20 | 1 |
| 1 | 23.08 | 2.5 | 2 | 8 | 4 | 1.085 | 1 | 1 | 11 | 1 | 2 | 60 | 2185 | 1 |
| 1 | 27 | 0.75 | 2 | 8 | 8 | 2.229175258 | 1 | 1 | 3 | 1 | 2 | 312 | 151 | 1 |
| 0 | 20.42 | 10.5 | 1 | 14 | 8 | 0 | 0 | 0 | 0 | 1 | 2 | 154 | 33 | 0 |
| 1 | 52.33 | 1.375 | 1 | 8 | 8 | 9.46 | 1 | 0 | 2.424597365 | 1 | 2 | 200 | 101 | 0 |
| 1 | 23.08 | 11.5 | 2 | 9 | 8 | 2.125 | 1 | 1 | 11 | 1 | 2 | 290 | 285 | 1 |
| 1 | 42.83 | 1.25 | 2 | 7 | 4 | 13.875 | 0 | 1 | 1 | 1 | 2 | 352 | 113 | 0 |
| 1 | 74.83 | 19 | 1 | 1 | 1 | 0.04 | 0 | 1 | 2 | 0 | 2 | 0 | 352 | 0 |
| 1 | 25 | 4.721637298 | 2 | 6 | 4 | 3 | 1 | 0 | 0 | 1 | 2 | 20 | 1 | 1 |
| 1 | 39.58 | 13.915 | 2 | 9 | 4 | 8.625 | 1 | 1 | 6 | 1 | 2 | 70 | 1 | 1 |
| 0 | 47.75 | 8 | 2 | 8 | 4 | 7.875 | 1 | 1 | 6 | 1 | 2 | 0 | 1261 | 1 |
| 0 | 47.42 | 3 | 2 | 14 | 4 | 13.875 | 1 | 1 | 2 | 1 | 2 | 519 | 1705 | 1 |
| 1 | 23.17 | 0 | 2 | 13 | 4 | 0.085 | 1 | 0 | 2.424597365 | 0 | 2 | 0 | 1 | 1 |
| 1 | 22.58 | 1.5 | 1 | 6 | 4 | 0.54 | 0 | 0 | 0 | 1 | 2 | 120 | 68 | 0 |
| 1 | 26.75 | 1.125 | 2 | 14 | 8 | 1.25 | 1 | 0 | 0 | 0 | 2 | 0 | 5299 | 1 |
| 1 | 63.33 | 0.54 | 2 | 8 | 4 | 0.585 | 1 | 1 | 3 | 1 | 2 | 180 | 1 | 0 |
| 1 | 23.75 | 0.415 | 1 | 8 | 4 | 0.04 | 0 | 1 | 2 | 0 | 2 | 128 | 7 | 0 |
- 请使用StandardScaler对波士顿房价数据集进行零-均值规范化。
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
print(X_scaled)
print(X_scaled.shape)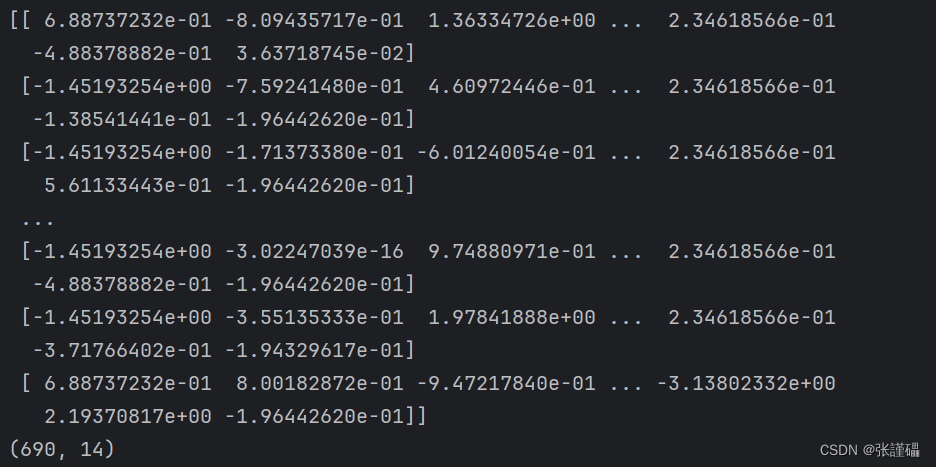
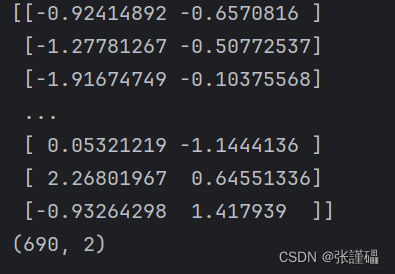
- 在上一问规范化后的数据基础上使用PCA对数据进行降维处理(降维后的特征数量为2)。
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
print(X_pca)
print(X_pca.shape)