Problem: 372. 超级次方
文章目录
- 题目描述
- 思路
- 复杂度
- Code
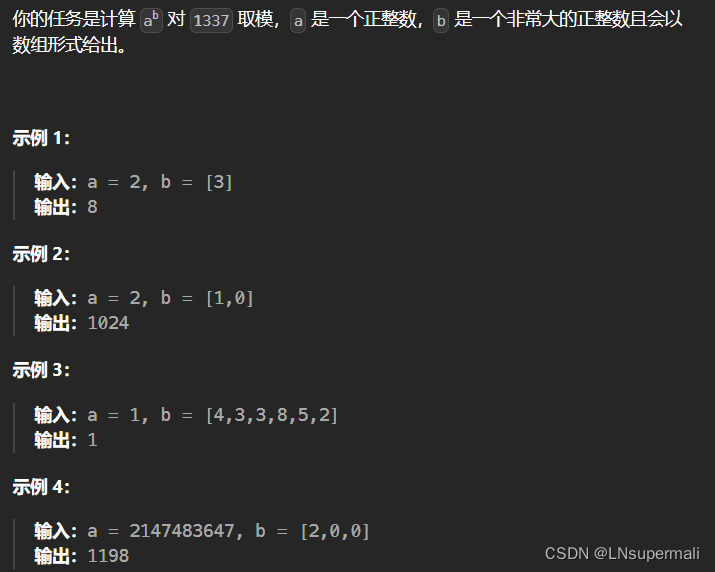
题目描述
思路
1.处理数组指数:如下图可以将其转换为一个递归的操作
2.处理 mod 运算:对于模运算我们有公式: ( a × b ) % k = ( a % k ) × ( b % k ) % k (a \times b) \% k = (a \% k) \times (b \% k) \% k (a×b)%k=(a%k)×(b%k)%k;则进一步得到k次幂的模运算为 ( a k ) % base = ( ( a % base ) k ) % base (a^k) \% \text{base} = ((a \% \text{base})^k) \% \text{base} (ak)%base=((a%base)k)%base;结合下图快速幂计算:
复杂度
时间复杂度:
O ( n × l o g k ) O(n \times logk) O(n×logk);其中 n n n为数组b的长度, k k k为数组b中的最大值
空间复杂度:
O ( n + l o g k ) O(n + logk) O(n+logk)
Code
class Solution {
private int base = 1337;
/**
* Super Pow
*
* @param a Base a
* @param b Exponent b
* @return int
*/
public int superPow(int a, int[] b) {
if (b.length == 0) {
return 1;
}
int last = b[b.length - 1];
int[] newB = Arrays.copyOf(b, b.length - 1);
int part1 = myPow(a, last);
int part2 = myPow(superPow(a, newB), 10);
return (part1 * part2) % base;
}
/**
* Fast power calculation of a to the k power
*
* @param a Base a
* @param k Exponent k
* @return int
*/
private int myPow(int a, int k) {
if (k == 0) {
return 1;
}
a %= base;
//K is odd
if (k % 2 == 1) {
return (a * myPow(a, k - 1)) % base;
} else { //K is even
int sub = myPow(a, k / 2);
return (sub * sub) % base;
}
}
}


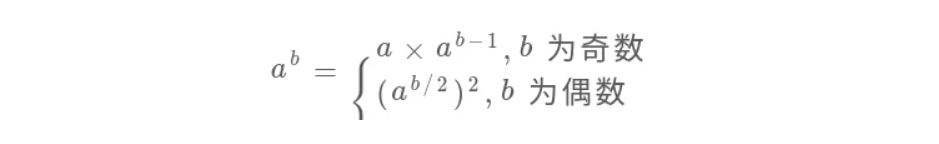
![[C++][数据结构][跳表]详细讲解](https://img-blog.csdnimg.cn/direct/041dd1f0035442a9a2020cf639326eea.png)