svm和决策树基本知识以及模型评价以及模型保存
文章目录
- 一、SVM
- 1.1,常用属性函数
- 二、决策树
- 2.1,常用属性函数
- 2.2,决策树可视化
- 2.3,决策树解释
- 3,模型评价
- 3.1,方面一(评价指标)
- 3.2,方面二(不同数据规模下,模型的性能)
- 4,模型保存与读取
- 4.1,模型的保存
- 4.2,模型的读取
一、SVM
1.1,常用属性函数
predict:返回一个数组表示个测试样本的类别。
predict_probe:返回一个数组表示测试样本属于每种类型的概率。
decision_function:返回一个数组表示测试样本到对应类型的超平面距离。
get_params:获取当前svm函数的各项参数值。
score:获取预测结果准确率。
set_params:设置SVC函数的参数 clf.n_support_:各类的支持向量的个数
clf.support_:各类的支持向量在训练样本中的索引
clf.support_vectors_:全部支持向量
原文链接:
二、决策树
2.1,常用属性函数
classes_:类标签(单输出问题)或类标签数组的列表(多输出问题)。
feature_importances_:特征重要度。
max_features_:max_features的推断值。
n_classes_:类数(用于单输出问题),或包含每个输出的类数的列表(用于多输出问题)。
n_features_:执行拟合时的特征数量。
n_outputs_:执行拟合时的输出数量。
tree_:训练(拟合):fit(train_x, train_y)
预测:predict(X)返回标签、predict_log_proba(X)、predict_proba(X)返回概率,每个点的概率和为1,一般取predict_proba(X)[:,1]
评分(返回平均准确度):score(test_x, test_y)。等效于准确率accuracy_score
参数类:获取分类器的参数get_params([deep])、设置分类器的参数set_params(params)。
原文链接:
2.2,决策树可视化
from sklearn.datasets import load_iris
from sklearn import tree
import matplotlib.pyplot as plt
# 加载鸢尾花数据集
iris = load_iris()
# 创建决策树模型
model = tree.DecisionTreeClassifier(max_depth=2)
model.fit(iris.data, iris.target)
# 可视化决策树
feature_names = iris.feature_names
plt.figure(figsize=(12,12))
_ = tree.plot_tree(model, feature_names=feature_names, class_names=iris.target_names, filled=True, rounded=True)
plt.show()
2.3,决策树解释
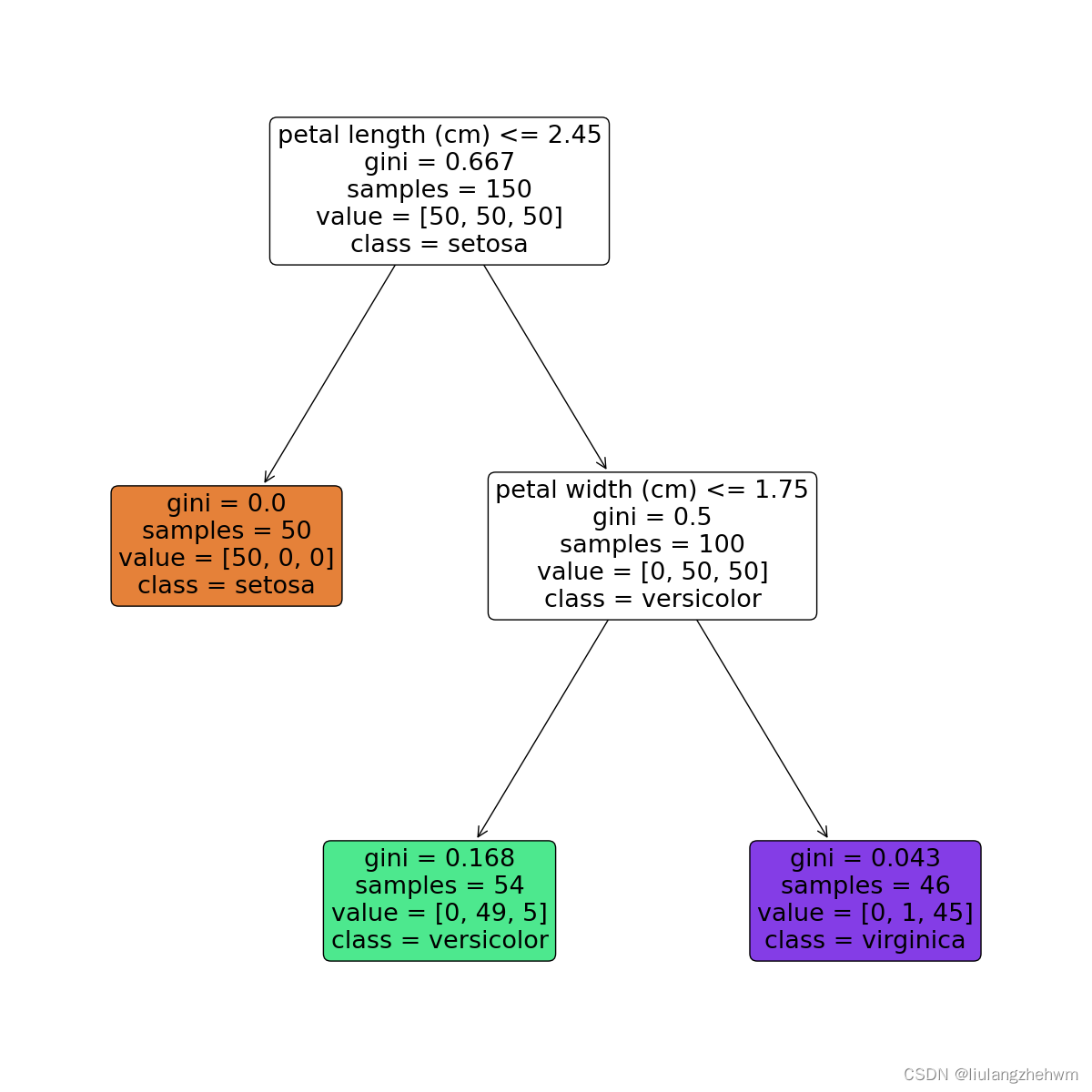
节点含义:
- petal length (cm)<=2.45表示数据特征petal width (cm)<=0.75,当petal width (cm)<=0.75,进入左边分支,否则进入右边分支;
- gini表示该节点的基尼系数;
- samples表示该节点的样本数;
- value表示各分类的样本数,例如,根节点中的[34,32,39]表示分类为Setosa的样本数为34,分类为Versicolour的样本数为32,分类为Virginica的样本数量为39;
- class表示该区块被划分为的类别,它是由value中样本数较多的类别决定的,例如,根节点中分类为Virginica的样本数最多,所以该节点的分类为Virginica,依此类推。
每一个颜色代表一个分类,随着层数的增加,颜色也会变深。
原文链接
3,模型评价
3.1,方面一(评价指标)
- 准确率
准确率是分类问题中最常用的评估指标,用于衡量模型的正确预测率。 - 精确率和召回率
精确率和召回率用于评估二分类模型的性能。精确率是指预测为正例的样本中实际为正例的比例,召回率是指实际为正例的样本中被正确预测为正例的比例。 - F1分数
F1分数是精确率和召回率的加权平均值,用于评估二分类模型的性能。
# 其他的指标
def accuracy_precision_recall_f1(y_true, y_pred):
# 1.准确率
accuracy = accuracy_score(y_true, y_pred)
# 2.精确率和召回率
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
# 3.F1分数
f1 = f1_score(y_true, y_pred)
return [accuracy, precision, recall, f1]
print(accuracy_precision_recall_f1(test_label_shulle_scaler, test_data_predict))
原文链接
- 混淆矩阵
混淆矩阵是一个二维矩阵,用于表示分类模型的性能。它将预测结果分为真正例(True Positive)、假正例(False Positive)、真反例(True Negative)和假反例(False Negative)四类,分别对应矩阵的四个象限。
def draw_confusion_matrix(label_true, label_pred, label_name, normlize, title="Confusion Matrix", pdf_save_path=None,
dpi=100):
"""
@param label_true: 真实标签,比如[0,1,2,7,4,5,...]
@param label_pred: 预测标签,比如[0,5,4,2,1,4,...]
@param label_name: 标签名字,比如['cat','dog','flower',...]
@param normlize: 是否设元素为百分比形式
@param title: 图标题
@param pdf_save_path: 是否保存,是则为保存路径pdf_save_path=xxx.png | xxx.pdf | ...等其他plt.savefig支持的保存格式
@param dpi: 保存到文件的分辨率,论文一般要求至少300dpi
@return:
example:
draw_confusion_matrix(label_true=y_gt,
label_pred=y_pred,
label_name=["Angry", "Disgust", "Fear", "Happy", "Sad", "Surprise", "Neutral"],
normlize=True,
title="Confusion Matrix on Fer2013",
pdf_save_path="Confusion_Matrix_on_Fer2013.png",
dpi=300)
"""
cm1 = confusion_matrix(label_true, label_pred)
cm = confusion_matrix(label_true, label_pred)
print(cm)
if normlize:
row_sums = np.sum(cm, axis=1)
cm = cm / row_sums[:, np.newaxis]
cm = cm.T
cm1 = cm1.T
plt.imshow(cm, cmap='Blues')
plt.title(title)
# plt.xlabel("Predict label")
# plt.ylabel("Truth label")
plt.xlabel("预测标签")
plt.ylabel("真实标签")
plt.yticks(range(label_name.__len__()), label_name)
plt.xticks(range(label_name.__len__()), label_name, rotation=45)
plt.tight_layout()
plt.colorbar()
for i in range(label_name.__len__()):
for j in range(label_name.__len__()):
color = (1, 1, 1) if i == j else (0, 0, 0) # 对角线字体白色,其他黑色
value = float(format('%.1f' % (cm[i, j] * 100)))
value1 = str(value) + '%\n' + str(cm1[i, j])
plt.text(i, j, value1, verticalalignment='center', horizontalalignment='center', color=color)
plt.show()
# if not pdf_save_path is None:
# plt.savefig(pdf_save_path, bbox_inches='tight', dpi=dpi)
labels_name = ['健康', '故障']
test_data_predict = SVC_all.predict(test_data_shuffle_scaler)
draw_confusion_matrix(label_true=test_label_shulle_scaler,
label_pred=test_data_predict,
label_name=labels_name,
normlize=True,
title="混淆矩阵",
# title="Confusion Matrix",
pdf_save_path="Confusion_Matrix.jpg",
dpi=300)
原文链接
- AUC和ROC曲线
ROC曲线是一种评估二分类模型性能的方法,它以真正例率(TPR)为纵轴,假正例率(FPR)为横轴,绘制出模型预测结果在不同阈值下的性能。AUC是ROC曲线下面积,用于评估模型总体性能。
# 画ROC曲线函数
def plot_roc_curve(y_true, y_score):
"""
y_true:真实值
y_score:预测概率。注意:不要传入预测label!!!
"""
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
fpr, tpr, threshold = roc_curve(y_true, y_score)
# plt.xlabel('False Positive Rate')
# plt.ylabel('Ture Positive Rate')
plt.xlabel('特异度')
plt.ylabel('灵敏度')
plt.title('ROC曲线')
# plt.title('roc curve')
plt.plot(fpr, tpr, color='b', linewidth=0.8)
plt.plot([0, 1], [0, 1], 'r--')
plt.show()
# print(np.sum(SVC_all.predict(test_data_shuffle_scaler)))
test_data_score = SVC_all.decision_function(test_data_shuffle_scaler)
plot_roc_curve(test_label_shulle_scaler, SVC_all.predict_proba(test_data_shuffle_scaler)[:,1])
plot_roc_curve(test_label_shulle_scaler, test_data_score)
# 计算AUC
from sklearn.metrics import roc_auc_score
print(roc_auc_score(test_label_shulle_scaler, SVC_all.predict_proba(test_data_shuffle_scaler)[:,1]))
原文链接
3.2,方面二(不同数据规模下,模型的性能)
def plot_learning_curve(estimator, title, X, y,
ax, # 选择子图
ylim=None, # 设置纵坐标的取值范围
cv=None, # 交叉验证
n_jobs=None # 设定索要使用的线程
):
train_sizes, train_scores, test_scores = learning_curve(estimator, X, y
, cv=cv, n_jobs=n_jobs)
# learning_curve() 是一个可视化工具,用于评估机器学习模型的性能和训练集大小之间的关系。它可以帮助我们理解模型在不同数据规模下的训练表现,
# 进而判断模型是否出现了欠拟合或过拟合的情况。该函数会生成一条曲线,横轴表示不同大小的训练集,纵轴表示训练集和交叉验证集上的评估指标(例如
# 准确率、损失等)。通过观察曲线,我们可以得出以下结论:
# 1,训练集误差和交叉验证集误差之间的关系:当训练集规模较小时,模型可能过度拟合,训练集误差较低,交叉验证集误差较高;当训练集规模逐渐增大时,
# 模型可能更好地泛化,两者的误差逐渐趋于稳定。
# 2,训练集误差和交叉验证集误差对训练集规模的响应:通过观察曲线的斜率,我们可以判断模型是否存在高方差(过拟合)或高偏差(欠拟合)的问题。如果
# 训练集和交叉验证集的误差都很高,且二者之间的间隔较大,说明模型存在高偏差;如果训练集误差很低而交叉验证集误差较高,且二者的间隔也较大,说
# 明模型存在高方差。
# cv : int:交叉验证生成器或可迭代的可选项,确定交叉验证拆分策略。v的可能输入是:
# - 无,使用默认的3倍交叉验证,
# - 整数,指定折叠数。
# - 要用作交叉验证生成器的对象。
# - 可迭代的yielding训练/测试分裂。
# ShuffleSplit:我们这里设置cv,交叉验证使用ShuffleSplit方法,一共取得100组训练集与测试集,
# 每次的测试集为20%,它返回的是每组训练集与测试集的下标索引,由此可以知道哪些是train,那些是test。
# n_jobs : 整数,可选并行运行的作业数(默认值为1)。windows开多线程需要
ax.set_title(title)
if ylim is not None:
ax.set_ylim(*ylim)
# *是可以接受任意数量的参数
# 而 ** 可以接受任意数量的指定键值的参数
# def m(*args,**kwargs):
# print(args)
# print(kwargs)
# m(1,2,a=1,b=2)
# #args:(1,2),kwargs:{'b': 2, 'a': 1}
ax.set_xlabel("Training examples")
ax.set_ylabel("Score")
ax.grid() # 显示网格作为背景,不是必须
ax.plot(train_sizes, np.mean(train_scores, axis=1), 'o-'
, color="r", label="Training score")
ax.plot(train_sizes, np.mean(test_scores, axis=1), 'o-'
, color="g", label="Test score")
ax.legend(loc="best")
return ax
#
# y = y.astype(np.int)
print(X.shape)
print(y.shape)
title = ["Naive_Bayes", "DecisionTree", "SVM_RBF_kernel", "RandomForest", "Logistic"]
# model = [GaussianNB(), DTC(), SVC(gamma=0.001)
# , RFC(n_estimators=50), LR(C=0.1, solver="lbfgs")]
model = [GaussianNB(), DTC(), SVC(kernel="rbf")
, RFC(n_estimators=50), LR(C=0.1, solver="liblinear")]
cv = ShuffleSplit(n_splits=10, test_size=0.5, random_state=0)
# n_splits:
# 划分数据集的份数,类似于KFlod的折数,默认为10份
# test_size:
# 测试集所占总样本的比例,如test_size=0.2即将划分后的数据集中20%作为测试集
# random_state:
# 随机数种子,使每次划分的数据集不变
# train_sizes: 随着训练集的增大,选择在10%,25%,50%,75%,100%的训练集大小上进行采样。
# 比如(CV= 5)10%的意思是先在训练集上选取10%的数据进行五折交叉验证。
# train_sizes:数组类,形状(n_ticks),dtype float或int
# 训练示例的相对或绝对数量,将用于生成学习曲线。如果dtype为float,则视为训练集最大尺寸的一部分
# (由所选的验证方法确定),即,它必须在(0,1]之内,否则将被解释为绝对大小注意,为了进行分类,
# 样本的数量通常必须足够大,以包含每个类中的至少一个样本(默认值:np.linspace(0.1,1.0,5))
# 输出:
# train_sizes_abs:
# 返回生成的训练的样本数,如[ 10 , 100 , 1000 ]
# train_scores:
# 返回训练集分数,该矩阵为( len ( train_sizes_abs ) , cv分割数 )维的分数,
# 每行数据代表该样本数对应不同折的分数
# test_scores:
# 同train_scores,只不过是这个对应的是测试集分数
print("===" * 25)
fig, axes = plt.subplots(1, 5, figsize=(30, 6))
for ind, title_, estimator in zip(range(len(title)), title, model):
times = time()
plot_learning_curve(estimator, title_, X_scaler, y,
ax=axes[ind], ylim=[0, 1.05], n_jobs=4, cv=cv)
print("{}:{}".format(title_, datetime.datetime.fromtimestamp(time() - times).strftime(" %M:%S:%f")))
plt.show()
print("===" * 25)
for i in [*zip(range(len(title)), title, model)]:
print(i)
原文链接
4,模型保存与读取
4.1,模型的保存
title = ["Naive_Bayes", "DecisionTree", "SVM_RBF_kernel", "RandomForest", "Logistic"]
model = [GaussianNB(), DTC(), SVC(gamma=0.001)
, RFC(n_estimators=50), LR(C=0.1, solver="liblinear")]
import joblib
for i_index, i in enumerate(model):
i.fit(X, y)
joblib_file = "model_save/" + title[i_index] + "_model.pkl"
with open(joblib_file, 'wb') as file:
joblib.dump(i, joblib_file)
print(i.score(X, y))
4.2,模型的读取
title = ["Naive_Bayes", "DecisionTree", "SVM_RBF_kernel", "RandomForest", "Logistic"]
for i in title:
joblib_file = "model_save/" + i + "_model.pkl"
with open(joblib_file, "rb") as file:
model = joblib.load(file)
print(i, ": ", model.score(X, y))