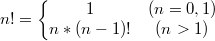在计算机控制系统中，某些系统为了避免控制作用过于频繁，消除由于频繁动作所引起的振荡，可采用带死区的PID控制算法，控制算式为：
式中，e(k)为位置跟踪偏差;e为一个可调参数，其具体数值可根据实际控制对象由实验确定。若e,值太小，会使控制动作过于频繁，达不到稳定被控对象的目的;若e值太大,则系统将产生较大的滞后。
带死区的控制系统实际上是一个非线性系统，当|e(k)|≤|e0|时，数字调节器输出为零;当|e(k)|> |e0|时，数字输出调节器有PID 输出。带死区的PID控制算法流程图如图1所示。
仿真实例：
被控对象为：
样时间为1ms ，对象输出上有一个幅值为0.5的正态分布的随机干扰信号。采用积分分离式 PID控制算法进行阶跃响应，取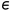 
=0.20，死区参数e=0.10，采用低通滤波器对对象输出信号进行滤波，滤波器为：
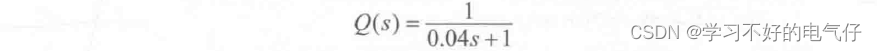
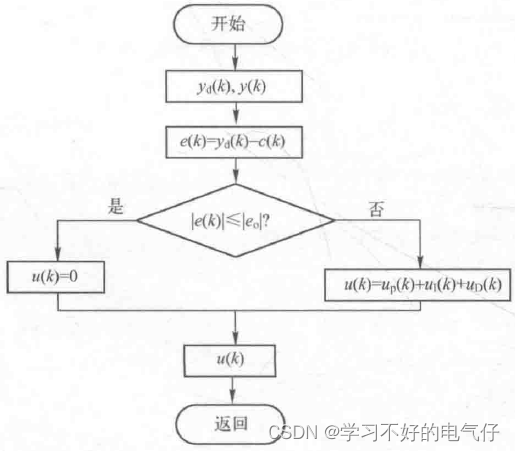
图1 带死区的PID控制算法程序框图
取M =1，采用一般积分分离式 PID控制方法，其控制结果如图2所示。取M =2，采用带死区的积分分离式PID控制方法，其控制结果如图3所示。由仿真结果可以看出，引入带死区 PID控制后，控制器输出更加平稳。
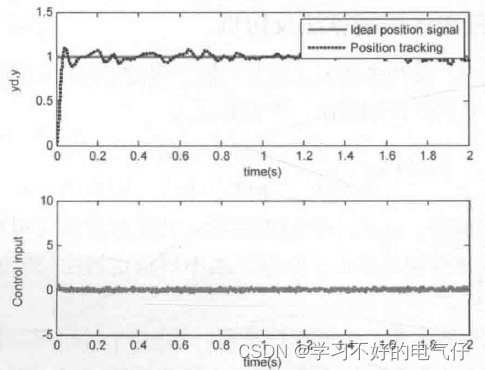
图2 不带死区PID控制（M=1）
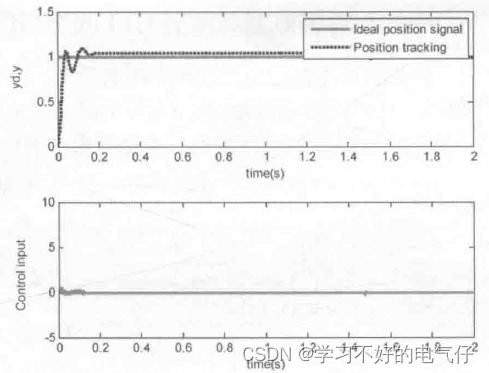
图2 带死区PID控制（M=2）
仿真程序：
clear all;
close all;
ts=0.001;
sys=tf(5.235e005,[1,87.35,1.047e004,0]);
dsys=c2d(sys,ts,'z);
[num,den]=tfdata(dsys,'v);
u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;
y 1=0;y_2=0；y_3=0；
yn_1=0;
error_1=0;error_ 2=0;ei=0;
sysl=tf([1].[0.04,1D): %Low Freq Signal Filter
dsys1=c2d(sys1,ts, tucsin');
[num1,denl]=tfdata(dsys1,'v);
f_1=0;
for k=1:1:2000
time(k)=k*ts;
yd(k)=1; %Step Signal
%Linear model
y(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*u_1+num(3)*u_2+num(4)*u_3;
n(k)=0.50*rands(1); %Noisy signal
yn(k)=y(k)+n(k);
%Low frequency filter
filty(k)=-den1(2)*f_1+numl(1)*(yn(k)+yn_1);
error(k)=yd(k)-filty(k);
if abs(error(k))<=0.20
ci=ei+error(k)*ts;
else
ei=0;
end
kp=0.50;ki=0.10;kd=0.020;
u(k)=kp*error(k)+ki*ei+kd*(error(k)-error1)/ts;
M=2;
if M==1
u(k)=u(k);
else if M==2 %Using Dead zone control
if abs(error(k))<=0.10
u(k)=0;
end
end
if u(k)>=10
u(k)=10;end
ifu(k)<=-10
u(k)=-10;end
%----------Return of PID parameters-------%
yd_1=yd(k);
u_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2；y_2=y_1；y_1=y(k);
f_1=filty(k);
yn1=yn(k);
error_ 2=error_1;error_1=error(k);
end
figure(1);subplot(211);
plot(time.yd,'r' time,y,'k:' linewidth',2);xlabel('time(s)');ylabel('yd,y');
legend('Ideal position signal','Position tracking');subplot(212);
plot(time,u,'r', linewidth ',2);
xlabel('time(s));ylabeI('Control input');figure(2);
plot(time,n,'r',linewidth' ,2);
xlabel('time(s)):ylabel('Noisy signal');
