C语言递归函数（递归调用）详解

news2024/11/16 9:22:49

一个函数在它的函数体内调用它自身称为递归调用，这种函数称为递归函数。执行递归函数将反复调用其自身，每调用一次就进入新的一层，当最内层的函数执行完毕后，再一层一层地由里到外退出。

递归函数不是C语言的专利，Java、C#、JavaScript、PHP 等其他编程语言也都支持递归函数。

下面我们通过一个求阶乘的例子，看看递归函数到底是如何运作的。阶乘 n! 的计算公式如下：

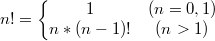
根据公式编写如下的代码：

#include<stdio.h>

//求n的阶乘
longfactorial(int n){
if(n ==0|| n ==1){
return1;
}
else{
returnfactorial(n -1)* n;// 递归调用
}
}

intmain(){
int a;
printf("Input a number: ");
scanf("%d",&a);
printf("Factorial(%d) = %ld\n", a,factorial(a));

return0;
}

运行结果：

Input a number: 5↙

Factorial(5) = 120

factorial() 就是一个典型的递归函数。调用 factorial() 后即进入函数体，只有当 n==0 或 n==1 时函数才会执行结束，否则就一直调用它自身。

由于每次调用的实参为 n-1，即把 n-1 的值赋给形参 n，所以每次递归实参的值都减 1，直到最后 n-1 的值为 1 时再作递归调用，形参 n 的值也为1，递归就终止了，会逐层退出。

要想理解递归函数，重点是理解它是如何逐层进入，又是如何逐层退出的，下面我们以 5! 为例进行讲解。

递归的进入

1) 求 5!，即调用 factorial(5)。当进入 factorial() 函数体后，由于形参 n 的值为 5，不等于 0 或 1，所以执行factorial(n-1) * n，也即执行factorial(4) * 5。为了求得这个表达式的结果，必须先调用 factorial(4)，并暂停其他操作。换句话说，在得到 factorial(4) 的结果之前，不能进行其他操作。这就是第一次递归。

2) 调用 factorial(4) 时，实参为 4，形参 n 也为 4，不等于 0 或 1，会继续执行factorial(n-1) * n，也即执行factorial(3) * 4。为了求得这个表达式的结果，又必须先调用 factorial(3)。这就是第二次递归。

3) 以此类推，进行四次递归调用后，实参的值为 1，会调用 factorial(1)。此时能够直接得到常量 1 的值，并把结果 return，就不需要再次调用 factorial() 函数了，递归就结束了。

下表列出了逐层进入的过程

层次/层数	实参/形参	调用形式	需要计算的表达式	需要等待的结果
1	n=5	factorial(5)	factorial(4) * 5	factorial(4) 的结果
2	n=4	factorial(4)	factorial(3) * 4	factorial(3) 的结果
3	n=3	factorial(3)	factorial(2) * 3	factorial(2) 的结果
4	n=2	factorial(2)	factorial(1) * 2	factorial(1) 的结果
5	n=1	factorial(1)	1	无

递归的退出

当递归进入到最内层的时候，递归就结束了，就开始逐层退出了，也就是逐层执行 return 语句。

1) n 的值为 1 时达到最内层，此时 return 出去的结果为 1，也即 factorial(1) 的调用结果为 1。

2) 有了 factorial(1) 的结果，就可以返回上一层计算factorial(1) * 2的值了。此时得到的值为 2，return 出去的结果也为 2，也即 factorial(2) 的调用结果为 2。

3) 以此类推，当得到 factorial(4) 的调用结果后，就可以返回最顶层。经计算，factorial(4) 的结果为 24，那么表达式factorial(4) * 5的结果为 120，此时 return 得到的结果也为 120，也即 factorial(5) 的调用结果为 120，这样就得到了 5! 的值。

下表列出了逐层退出的过程

层次/层数	调用形式	需要计算的表达式	从内层递归得到的结果（内层函数的返回值）	表达式的值（当次调用的结果）
5	factorial(1)	1	无	1
4	factorial(2)	factorial(1) * 2	factorial(1) 的返回值，也就是 1	2
3	factorial(3)	factorial(2) * 3	factorial(2) 的返回值，也就是 2	6
2	factorial(4)	factorial(3) * 4	factorial(3) 的返回值，也就是 6	24
1	factorial(5)	factorial(4) * 5	factorial(4) 的返回值，也就是 24	120