目录
1.人工神经网络参数个数的计算
2.卷积神经网络卷积和池化的计算
知识表示
命题
谓词
谓词公式
1.连接词
2.量词
3.量词的辖域
逻辑等价式
范式
推理规则
全程量词和存在量词之间的关系
产生式
产生式系统
3.命题/谓词逻辑证明
1.
2.
3.
4.
5.
6.
7.
推理技术
自然演绎推理
归结演绎推理(归结反演)
4.谓词公式化为子句集的方法
1.
5.鲁宾孙归结原理
6.归结反演
1.
机器学习
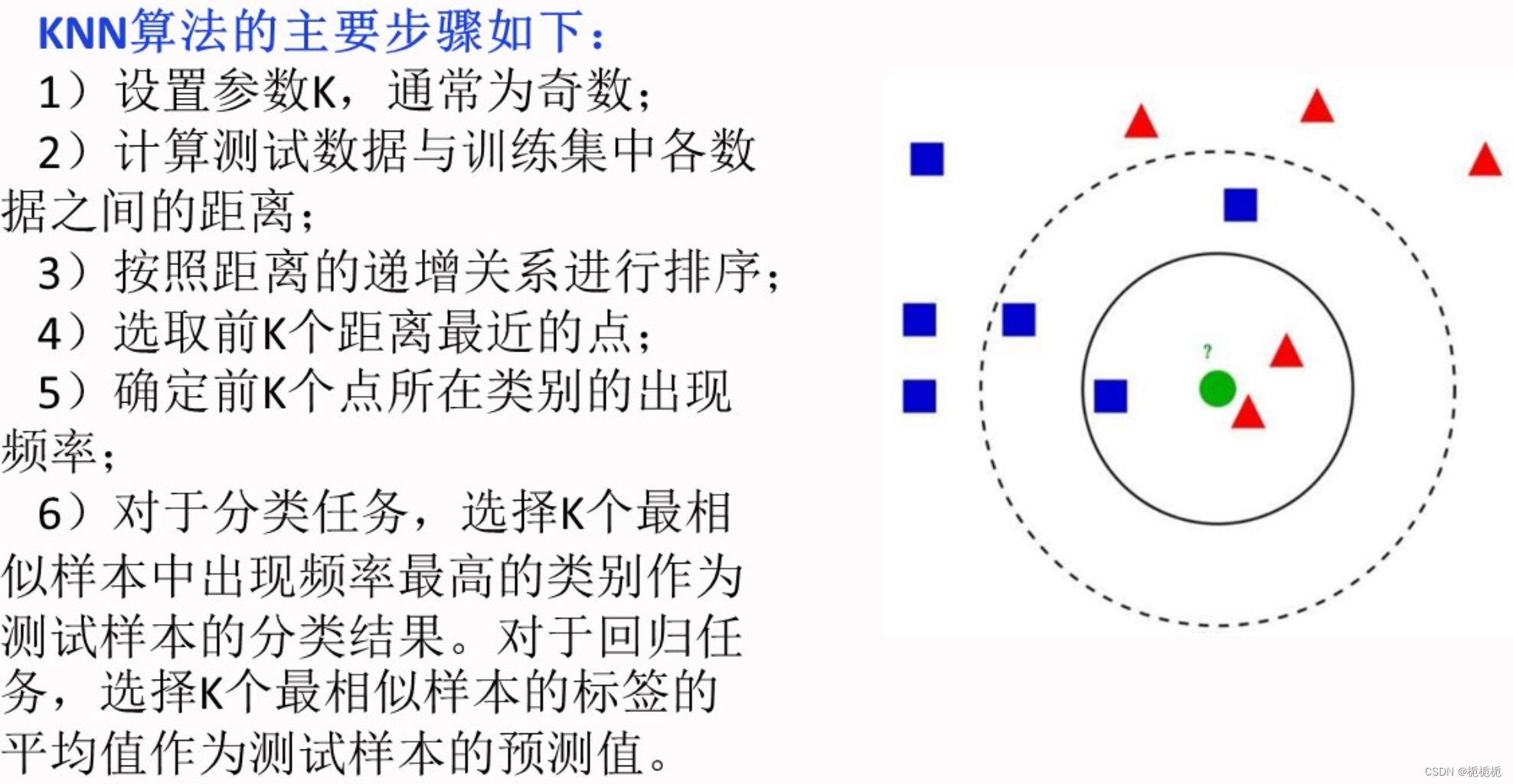
K-近邻算法
1.人工神经网络参数个数的计算
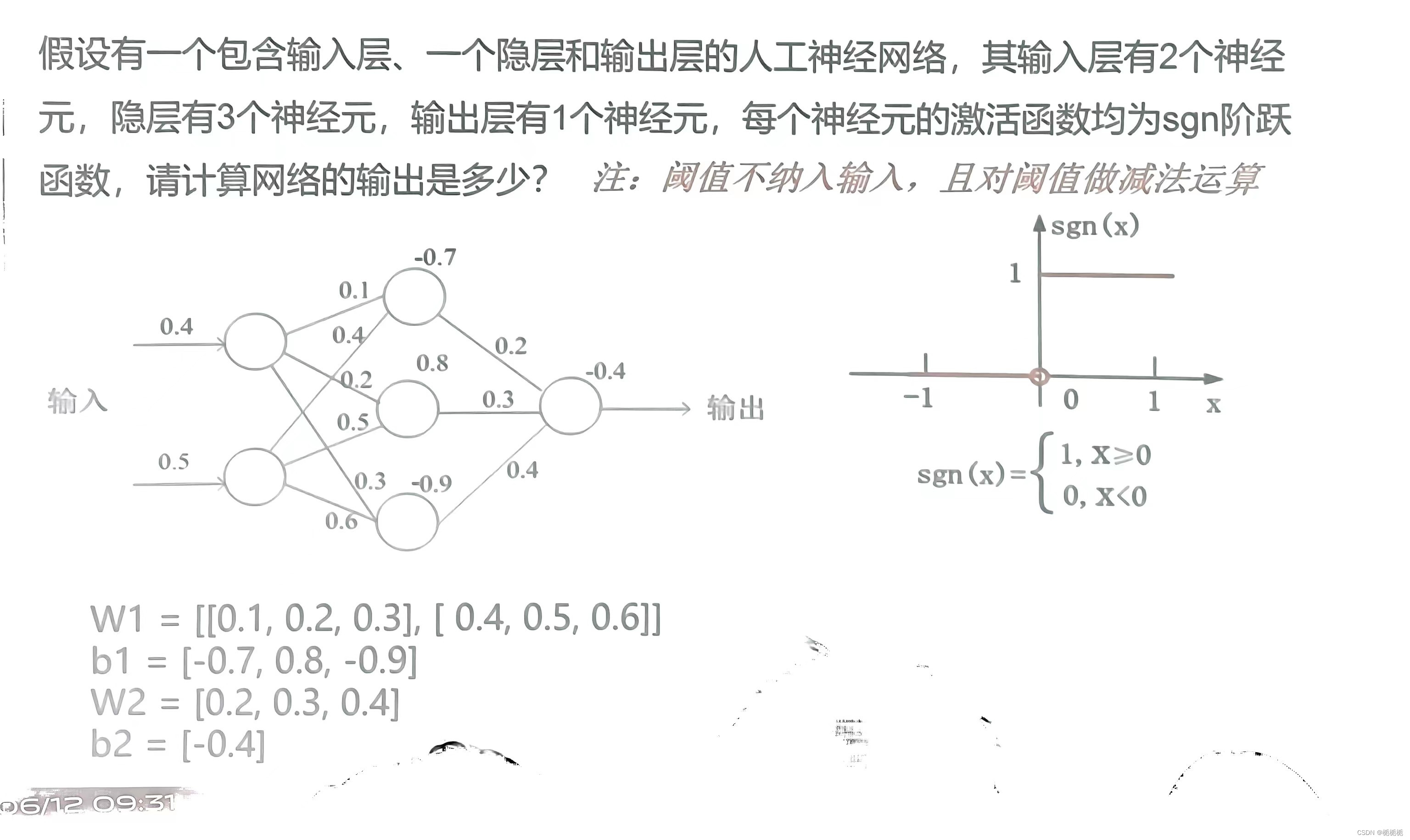

2.卷积神经网络卷积和池化的计算
!!!下面两篇大佬的高质量文(必看)!!!
卷积神经网络---详解卷积运算、池化操作(Pooling)_池化层操作流程-CSDN博客
深度学习CNN网络--卷积层、池化层、全连接层详解与其参数量计算_卷积层,池化层,全连接层-CSDN博客
卷积层:卷积运算、求输出图片的尺寸,卷积层参数m=k*k*c*n+n
池化层:最大池化、平均池化
知识表示
知识表示方法:逻辑表示法(命题逻辑和谓词逻辑)、产生式表示法
命题
命题是一个非真即假的陈述句。
判断一个句子是否为命题,首先应该判断它是否为陈述句,再判断它是否有唯一的真值。没有真假意义的语句(如感叹句,疑问句)不是命题。
一个命题不能同时既为真又为假,但可以在一种条件下为真,在另一种条件下为假。
简单陈述句表达的命题称为简单命题或原子命题。引入否定,合取,析取,条件,双条件等连接词,可以将原子命题构成复合命题。
谓词
一个谓词可以分为谓词名与个体两个部分。个体表示某个独立存在的事物或者某个抽象的概念;谓词名用于刻画个体的性质,状态,或个体间的关系。

谓词中包含的个体数目称为谓词的元数。P(x)是一元谓词,P(x,y)是二元谓词。
在谓词中,个体可以是常量,也可以是变元,还可以是一个函数。
函数可以递归调用。
谓词公式
谓词公式可以分为原子公式和合式公式。
无论是命题逻辑还是谓词逻辑,均可用下列连接词把一些简单命题连接起来成为一个复合命题,以表示一个比较复杂的含义。
1.连接词
否定、析取、合取、蕴含(或者条件)、等价(或者双条件)
2.量词
全称量词、存在量词
3.量词的辖域
位于量词后面的单个谓词或者用括号括起来的谓词公式称为量词的辖域,辖域内与量词中同名的变元称为约束变元,不受约束的变元称为自由变元。
逻辑等价式


范式
合取范式、析取范式
推理规则

全程量词和存在量词之间的关系
P(x)是谓词

产生式
1.确定性规则知识的产生式表示

2.不确定性规则知识的产生式表示

3.确定性事实性知识的产生式表示

4.不确定性事实性知识的产生式表示

产生式系统
一般来说,一个产生式系统由规则库,控制系统(推理机)、综合数据库三部分组成。
3.命题/谓词逻辑证明
1.

 2.
2.


3.


4.


5.


6.
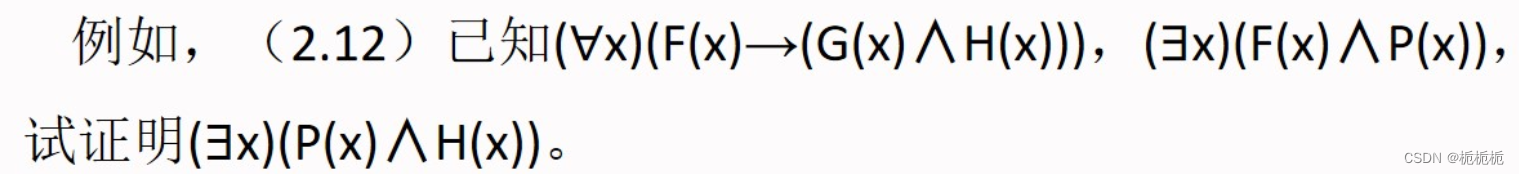

7.
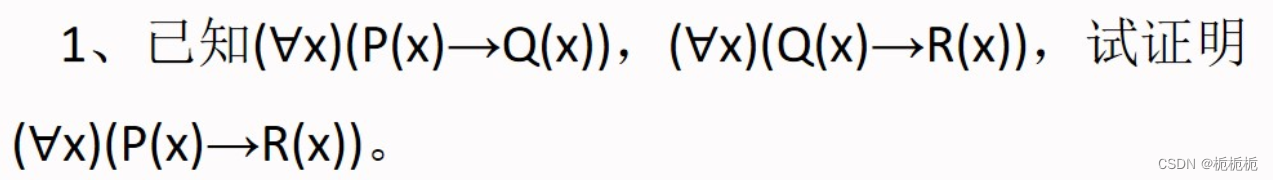

推理技术
从推出结论的途径来划分,推理可分为演绎推理、归纳推理、默认推理。
演绎推理:一般性知识推某一具体结论,一般到个别。
归纳推理:足够多事例归纳出一般性结论,个别到一般。
按推理时所用知识的确定性来划分,推理分为确定性推理和不确定性推理。
自然演绎推理
从一组已知为真的事实出发,直接运用经典逻辑推理的推理规则推出结论的过程称为自然演绎推理。其中,基本的推理是P规则,T规则,假言推理,拒取式推理等。

归结演绎推理(归结反演)

4.谓词公式化为子句集的方法
原子谓词公式:一个不能再分解的命题。
文字:原子谓词公式及其否定,统称为文字。P称为正文字,非P称为负文字。
字句:任何文字的析取式。任何文字本身也是字句。
空子句:不包含任何文字的字句,表示为NIL。(由于空子句含有文字,不能被任何解释满足,所以,空子句是永假的,不可满足的)
字句集:由字句构成的集合(字句的合取)。

1.


5.鲁宾孙归结原理
由谓词公式转化转化成字句集的过程可以看出,在子句集中子句之间是合取关系,其中只要有一个子句不可满足,则子句集就不可满足。由于空子句是不可满足的,所以,若一个子句集中包含空子句,则这个子句集一定是不可满足的。
鲁宾孙归结原理的基本方法:检查子句集S中是否包含空子句,若包含,则S不可满足;若不包含,就在子句集中选择合适的子句进行归结,一旦通过归结得到空子句,就说明子句集S是不可满足的。
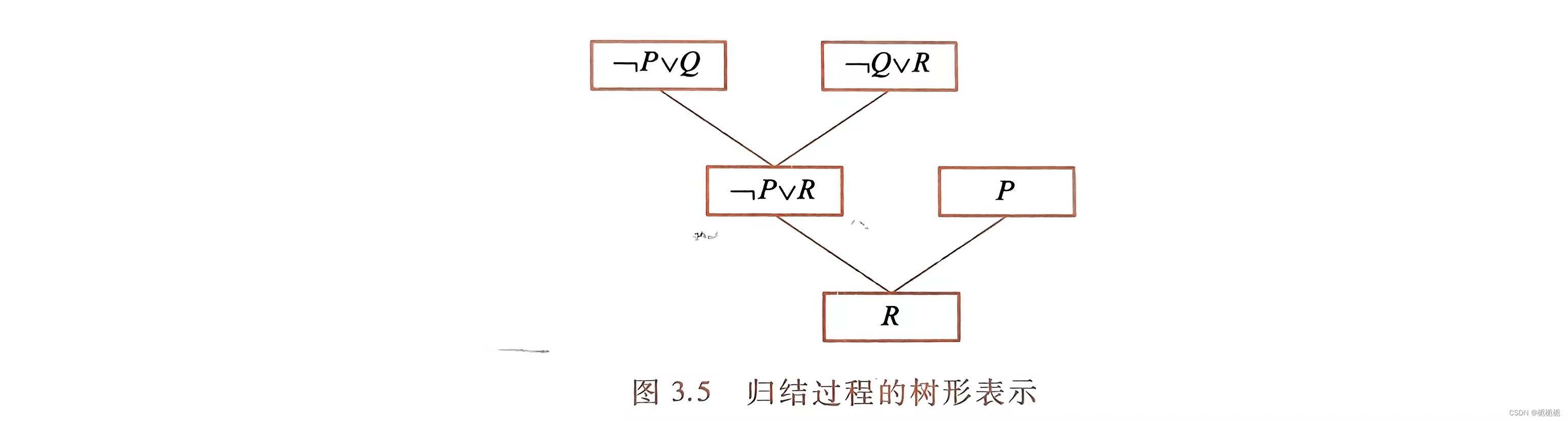
有的子句含变元,不能直接消去互补文字,需要先用最一般合一对变元进行代换,然后归结。

6.归结反演

归结原理可用于定理证明外,还可用来求取问题的答案。

1.



机器学习
机器学习分类(根据样本数据是否带有标签):监督的机器学习、无监督的机器学习、半监督学习。
监督学习又称为“有教师学习”。在监督学习中,模型采用有标签的数据集完成学习过程。
按任务的输出类型、监督学习可分为分类和回归两种。
无监督学习的特点是训练数据集中没有标签信息。
监督学习可完成分类和回归两种任务,非监督学习只能完成分类任务。
半监督学习介于二者之间,训练数据集只有一部分数据是有标签的,而其余的数据甚至大部分数据是没有标签的。
K-近邻算法