【答案解析】:
暴力破解:将
x
和
y
分别遍历
[1, n]
,进行判断当
x % y > k
时统计计数
count++
即可
,
但是这样的话当
n
的值非常大 的时候循环次数将非常恐怖,需要循环 n^2
次。
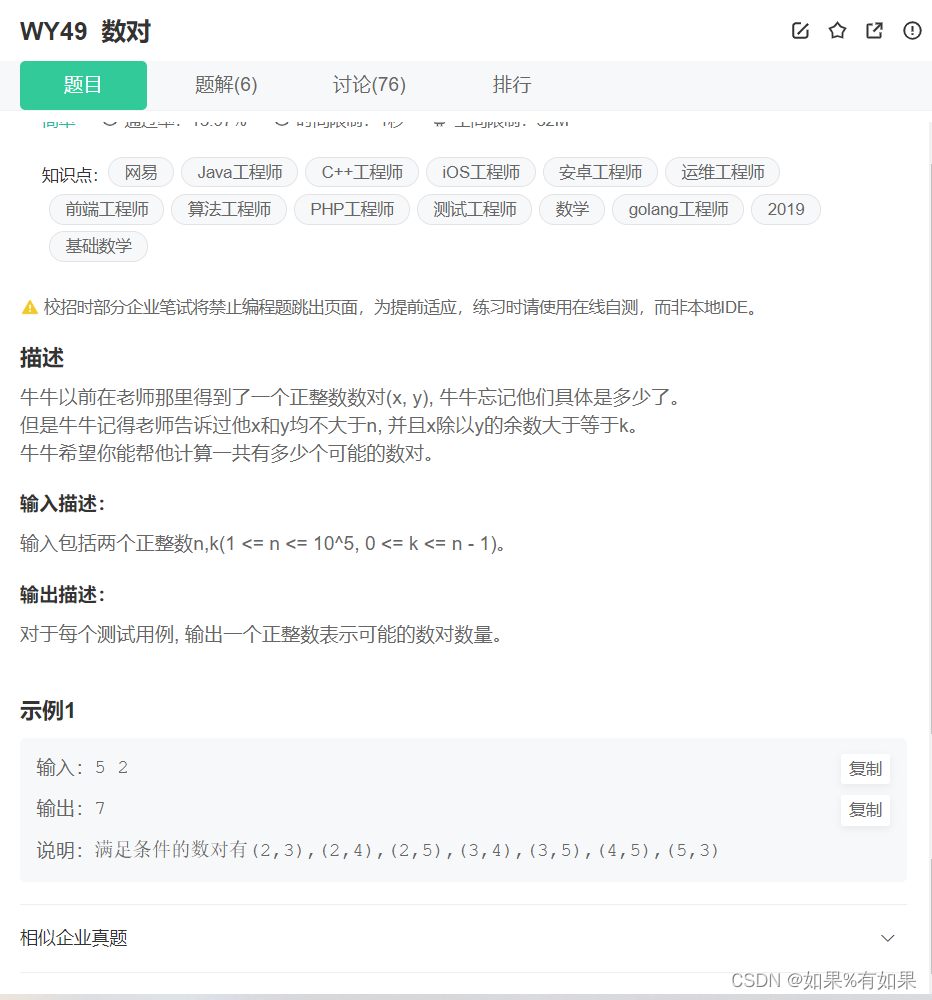
更优解法: 假设输入
n=10 , k=3
;
当
y <=k
时,意味着任何数字取模
y
的结果都在
[0, k-1]
之间,都是不符合条件的。
当
y = k+1=4
时,
x
符合条件的数字有
3,7
当
y = k+2=5
时,
x
符合条件的数字有
3,4,8,9
当
y = k+3=6
时,
x
符合条件的数字有
3,4,5,9,10
当
y = k+n
时,
x
小于
y
当前值,且符合条件的数字数量是:
y-k
个,
x
大于
y
当前值,小于
2*y
的数据中,且符合条件的数字数量是:
y-k
个
从上一步能看出来,在
y
的整数倍区间内,
x
符合条件的数量就是
(n / y) * (y - k)
个
n / y
表示有多少个完整的
0 ~ y
区间,
y - k
表示有每个区间内有多少个符合条件的数字
最后还要考虑的是
6...
往后这种超出倍数区间超过
n
的部分的统计
n % y
就是多出完整区间部分的数字个数,其中
k
以下的不用考虑,则符合条件的是
n % y - (k-1)
个
这里需要注意的是类似于
9
这种超出完整区间的数字个数 本就小于
k
的情况,则为
0
最终公式:(n / y) * (y - k)+ ((n % y < k) ? 0, (n % y - k + 1));
本人代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
int main()
{
long n, k = 0;
long count = 0;
while (~scanf("%ld %ld", &n, &k))
{
if (k == 0) //特殊情况考虑
{
printf("%ld\n", n * n);
continue;
}
for (long j = k + 1; j <= n; j++) //今天见上文分析
{
long help = n % j < k ? 0 : (n % j) - k + 1;
count += (j - k) * (n / j) + help;
}
printf("%ld\n", count);
}
system("pause");
return 0;
}
答案代码:
#include <stdio.h>
int main()
{
long n, k;
while(~scanf("%ld %ld", &n, &k)){
if (k == 0) {
printf("%ld\n", n * n);//任意数对的取模结果都是大于等于0的
continue;
}
long count = 0;
for(long y = k + 1; y <= n; y++) {
count += ((n / y) * (y - k)) + ((n % y < k) ? 0 : (n % y - k + 1));
}
printf("%ld\n", count);
}
return 0;
}