python基础知识整理二

算法分析

运行时间检测

1. python中有一个time模块，可以获取计算机系统当前时间。在算法开始和结束后分别记录系统时间，即可得到运行时间。

import time
time.time()

2. 同一个算法，采用不同的编程语言编写，放在不同的机器上运行，得到的运行时间会不一样，有时候会大不一样。

大O表示法

• 问题规模是影响算法执行时间的主要因素，有些具体数据也会影响算法运行时间。
• 算法的分析看主流，不要被特定的几种运行状况迷惑。
• O(1)、O(n)、O(n的平方)、O(n的三次方)、O(logn)
  

“变位词”判断问题

1. 变位词是指两个词之间存在组成字母的重新排列问题，如earth和heart。

解法一: O(logn)

def a(s1, s2):
    ans = 0
    matches = True
    alist1 = list(s1)
    alist2 = list(s2)
    alist1.sort()
    alist2.sort()
    while ans < len(alist1) and matches:
        if alist1[ans] == alist2[ans]:
            ans += 1
        else:
            matches = False
    return matches

print(a('abcd', 'adcb'))

解法二：暴力法 O(n!)

解题思路：穷尽列举所有可能的组合，将s1中出现的字符全排列，再查看s2是否出现在全排列列表内。

解法三 O(n)

解题思路：为两个字符s1、s2各设置一个计数器，当26个字母出现的次数均相同，则说明它是变位词。

def a(s1, s2):
    pos1 = 0
    count1 = 0
    pos2 = 0
    count2 = 0
    for i in range(len(s1)):
        count1 = ord(s1[i])-ord('a')
        pos1 = count1 + pos1
        i += 1
    for i in range(len(s2)):
        count2 = ord(s2[i]) - ord('a')
        pos2 = count2 + pos2
        i += 1
    matches = True
    if pos1 == pos2:
        return True
    else:
        return False
print(a('abcd', 'adcb'))

Python数据类型的性能

列表list和字典dict，这是两种重要的python数据类型。

1. extend() 函数用于在列表末尾一次性追加另一个序列中的多个值。

2. list.insert(index, obj)
   参数： index：对象obj需要插入的索引位置, obj：要插入列表中的对象。
   

3. index()函数：查找字符串某个字符或字符串第一次出现的位置

4. cars.sort(reverse=True)，其中sort默认为升序排序

5. 当i缺省时，默认为0，即 a[:3]相当于 a[0:3]
   当j缺省时，默认为len(alist), 即a[1:]相当于a[1:10]
   当i,j都缺省时，a[:]就相当于完整复制一份a了

6. 切片操作
   

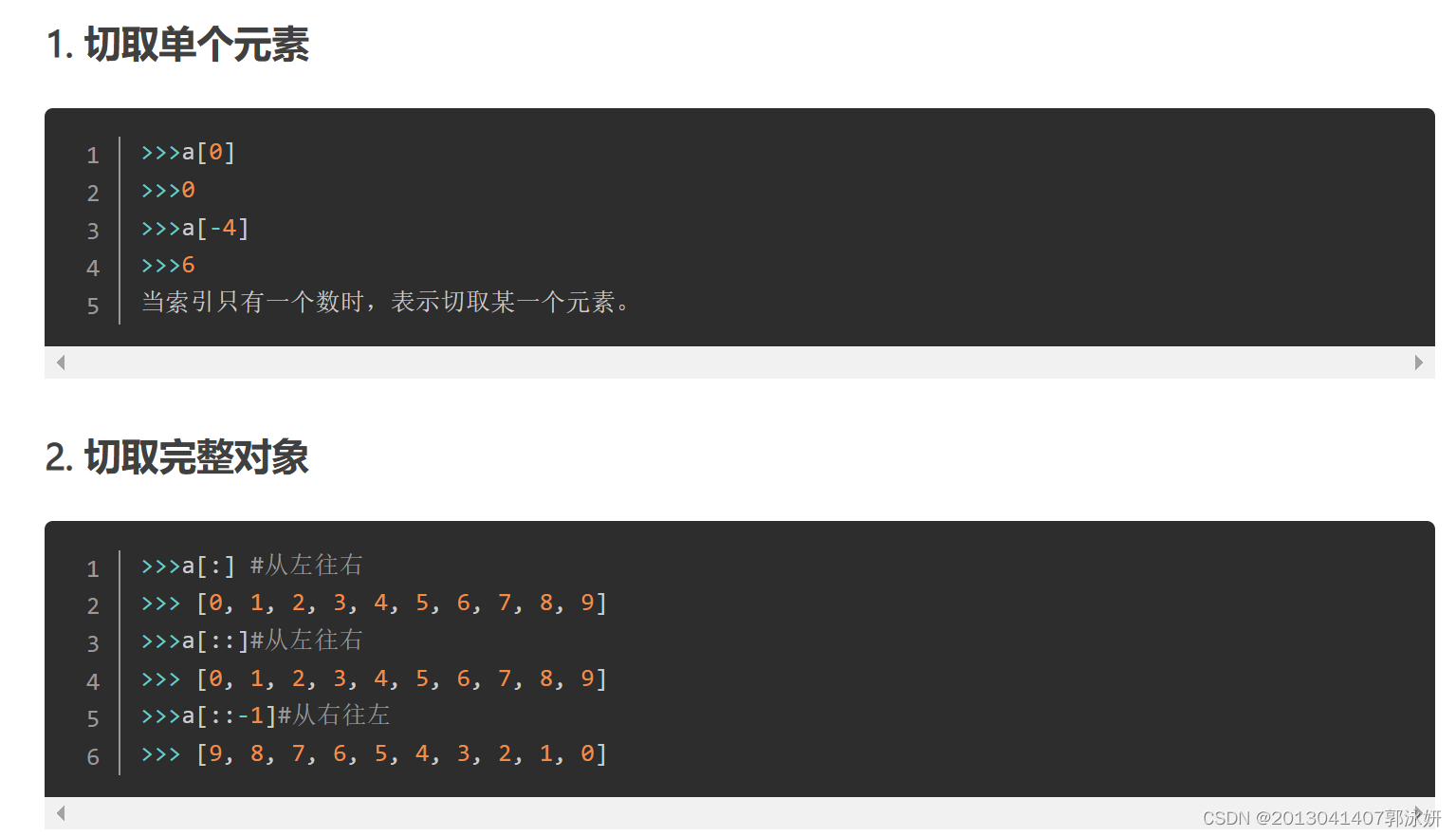
L = ['Michael', 'Sarah', 'Tracy', 'Bob', 'Jack']
>>> L[0:3]
['Michael', 'Sarah', 'Tracy']      ##L[0:3]表示，从索引0开始取，直到索引3为止，但不包括索引3。即索引0，1，2，正好是3个元素。

>>> L[:3]
['Michael', 'Sarah', 'Tracy']     ##如果第一个索引是0，还可以省略
>>> L[1:3]
['Sarah', 'Tracy']        ##从索引1开始，取出2个元素出来


>>> L[-2:]             ##倒数第一个元素的索引是-1
['Bob', 'Jack']         
>>> L[-2:-1]
['Bob']              ##倒切片

L = list(range(100))
>>> L
[0, 1, 2, 3, ..., 99]
L[:10]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]         ##前十个数
L[-10:]
[90, 91, 92, 93, 94, 95, 96, 97, 98, 99]     ##后十个数
>>> L[:10:2]
[0, 2, 4, 6, 8]          ##前10个数，每两个取一个
>>> L[::5]
[0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95]     ##所有数 每五个数取一个
>>> T = L[:]
T = [0, 1, 2, 3, ..., 99]       ##原样复制


>>> (0, 1, 2, 3, 4, 5)[:3]
(0, 1, 2)       ##tuple的切片操作，操作结果仍为tuple

>>> 'ABCDEFG'[:3]
'ABC'
>>> 'ABCDEFG'[::2]
'ACEG'          ##字符串的切片操作

6. 若想要得到的是切片的一份副本而非视图，就需要显式的进行复制操作函数copy()。
7. __contains__用法 【python 3.x无has_key()用法】

dict3 = {'name':'z','Age':7,'class':'First'};
print("Value : ",dict3.__contains__('name'))

Value : True

或者

dict3 = {'name': 'z', 'Age': 7, 'class': 'First'}
if "user_id" in dict3:
    print(dict3["user_id"])

8. update()函数，用 update 更新字典 a，会有两种情况：
   有相同的键时：会使用最新的字典 b 中 该 key 对应的 value 值。
   有新的键时：会直接把字典 b 中的 key、value 加入到 a 中。

a = {1: 2, 2: 2}
b = {1: 1, 3: 3}
a.update(b)
print(a)

{1: 1, 2: 2, 3: 3}

• 列表类型有很多操作，我们总的方案就是：让最常用的操作性能最好，牺牲不太常用的操作。
  
  

示例

判断是否是素数

1. 暴力法

n = int(input())
if n < 2:
    print("no")
for i in range(2, n):
    if n%i==0:
        print("不是素数")
        break
print("是素数")

2. 优化版

n = int(input())
def sushu(x):
    if x <=2 and x%2 == 0:  #判断是否为2且是否为偶数
        return "不是素数"
    else:
        for i in range(3,int(x**0.5)+1,2):
            if x%i == 0:
                return "不是素数"
    return "是素数"
print(sushu(n))

求素数个数

a = int(input())
b = int(input())
def sushu(x1,x2):
    count = 0
    for i in range(x1,x2+1):
        for j in range(2,i//2+1):
            if i%j == 0:     ## 重点代码
                break      
        else:
            count += 1
    print(count)
sushu(a,b)

基本结构——线性结构

1. 不同线性结构关键区别在于数据项增减的方式，有的结构只允许数据项从一端增加，而有的结构允许数据项从两端移除。
2. 四种数据结构栈Stack、队列Queue、双端队列Deque和列表List，这些数据集的共同点在于数据项只存在先后的次序关系，都是线性结构。
3. 这些线性结构是应用最广泛的数据结构，它们出现在各种算法中用来解决各种问题。

栈抽象数据类型以及Python实现

• 距离栈底越近的数据项，留在栈中的时间越长；而最新加入栈中的数据项会被最先移除，这种次序称为后进先出LIFO。

• 栈的特性：反转次序。
  
  

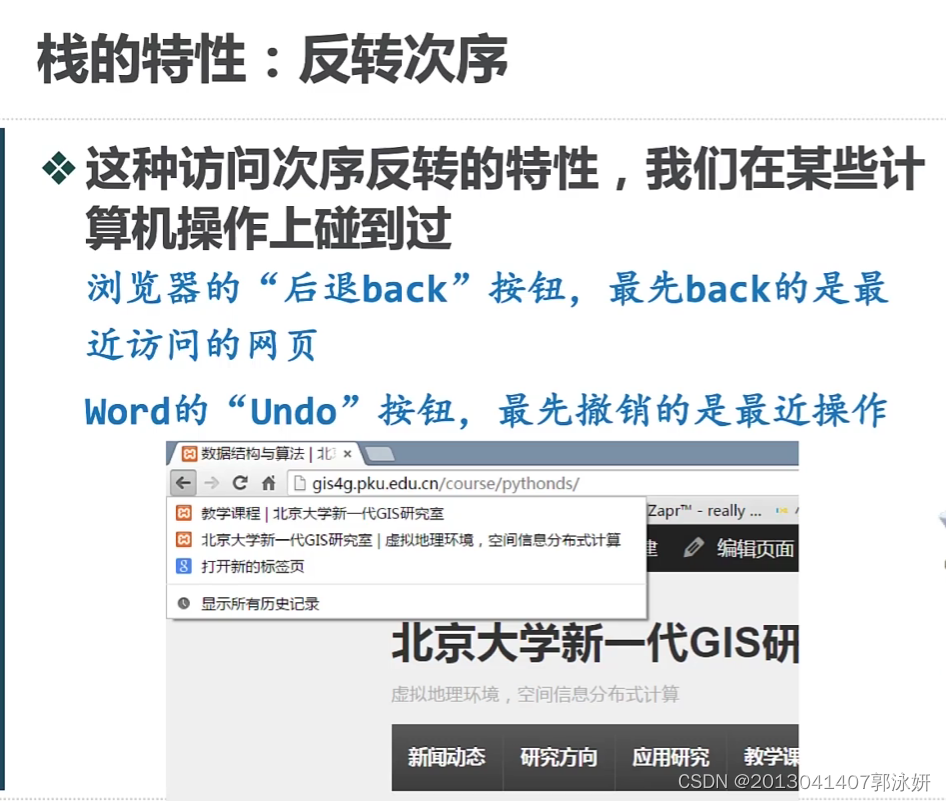
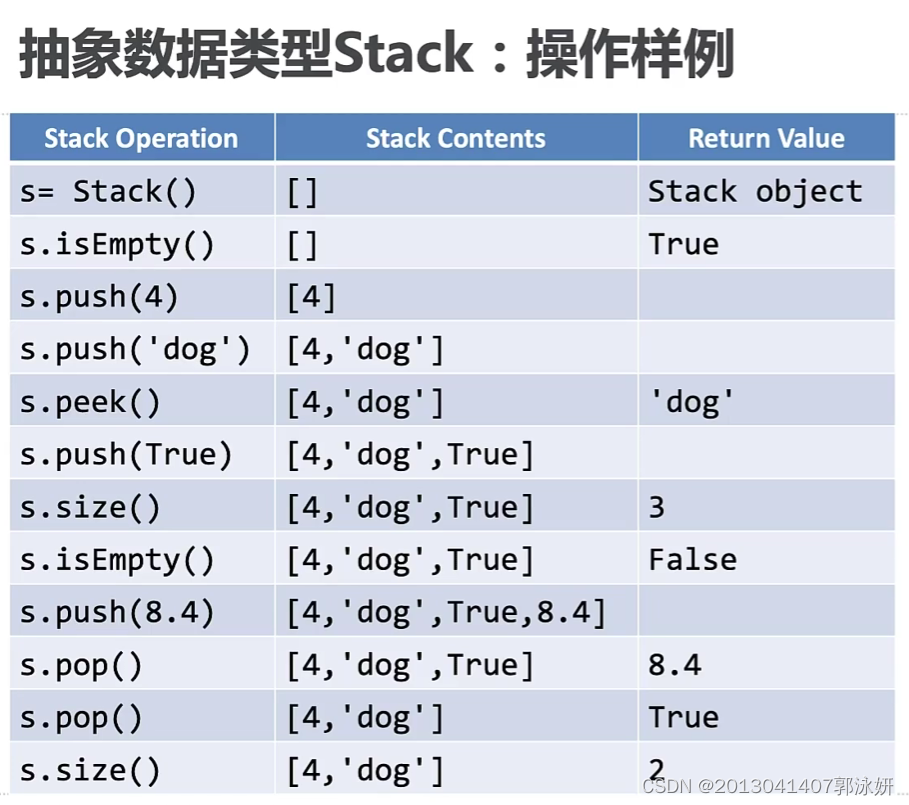
• stack1.peek() 返回栈顶元素，但不在堆栈中删除它。
  Stack2.pop() 返回栈顶元素，并在进程中删除它。

用Python实现抽象数据结构栈

1. Python的面向对象机制，可以用来实现用户自定义类型。
2. 将栈实现为Python的一个Class，将栈的操作方法实现为Class的方法。
3. 由于栈是一个数据集，所以我们采用Python的原生数据集List来实现。

栈的应用：简单括号匹配

• 每个开括号要恰好对应一个闭括号，对括号能否正确匹配的识别，是很多语言编译器的基础算法。
  
  Stack.py

class Stack(object):
    def __init__(self):
        # 定义一个空列表,相当于一个空栈,用来存储和读取
        self.stack = []
    #  用来检测长度
    def __len__(self):
        return len(self.stack)
    def top(self):
        # 判断栈是否为空
        if not self.is_empty():
            return self.stack[-1]
        # 抛出异常
        raise Exception('stack is empty!')
    def push(self,element):
        self.stack.append(element)
    def pop(self):
        # 判断栈是否为空
        if self.is_empty():
            raise Exception('stack is empty!')
        else:
            item = self.stack.pop()
            return item
    def length(self):
        return len(self.stack)
    def is_empty(self):
        return len(self.stack) == 0

StackTest.py

from Stack import Stack
def matches(open,close):
    opens="([{"
    closers=")]}"
    return opens.index(open)==closers.index(close)
def check(SymbolString):
    s = Stack()
    index = 0
    balanced = True
    while index<len(SymbolString) and balanced:
        symbol = SymbolString[index]
        if symbol == "([{":
            s.push(symbol)
        else:
            if s.is_empty():
                balanced = False
            else:
                top = s.pop()
                if not matches(top, symbol):
                    balanced = False
        index += 1
    if s.is_empty() and balanced:
        return True
    else:
        return False
print(check("(()))"))

括号匹配算法可以应用Stack的方法来处理，但并不是唯一的办法，也可以用Queue队列来实现

栈的应用：十进制转为二进制

1. 二进制是计算机原理中最基本的概念，作为组成计算机最基本部件的的逻辑门电路，其输入和输出均仅为两种状态：0和1。
   
   
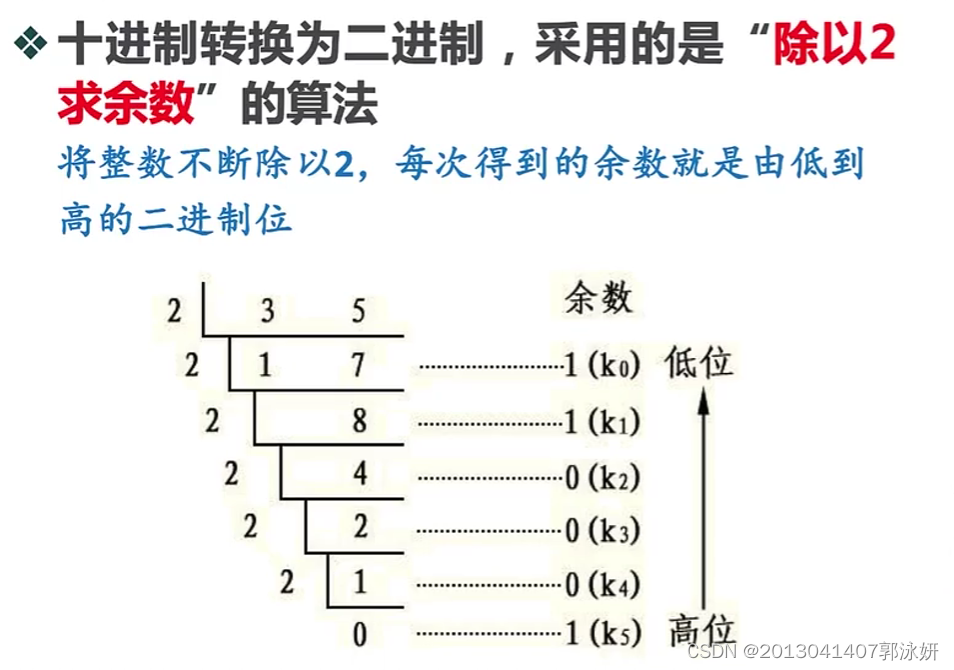
2. 除以2得到的余数从上往下的次序，但输出需要从下往上，这时候就需要栈结构来进行反转次序的操作。

from Stack import Stack
n = int(input())
def DecBin(n):
    remstack = Stack()
    while n>0:
        rem = n%2
        remstack.push(rem)
        n = n//2
    binString = ""
    while not remstack.is_empty():
        binString = binString+str(remstack.pop())
    return binString
print(DecBin(n))

3. 十进制转为N进制，只需要将“除以2求余数”的算法改为“除以N求余数”

4. 对于时钟来说是60进制。

表达式转换

1. 中缀表达式：a*b
2. 引入括号来强制优先级。
3. 全括号表达式：在所有表达式项两边都加上括号。
4. 前缀表达式：+AB， 后缀表达式：AB+
   
   
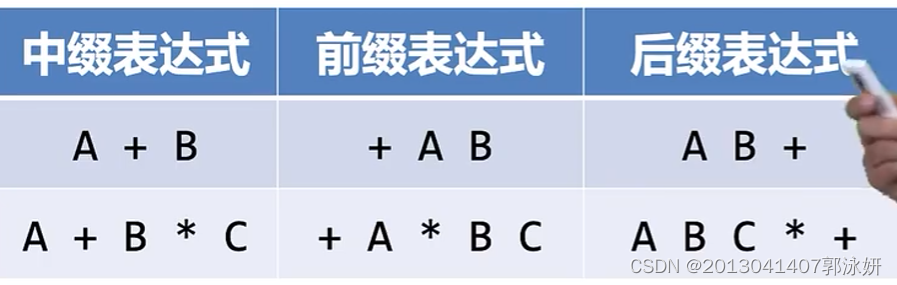
5. 在前缀和后缀表达式中，操作符的次序完全决定了运算的次序，离操作数越近的的操作符越先做。所以在很多情况下，表达式的计算机都尽量避免中缀表达式。
   

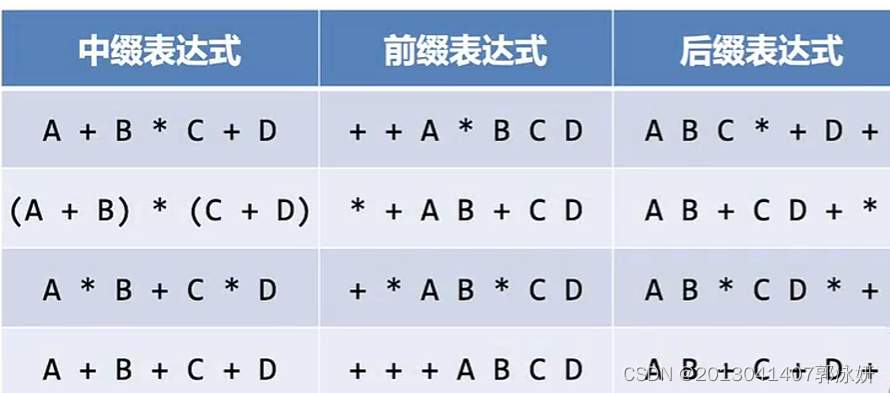
中缀表达式转换为前缀表达式和后缀表达式

看子表达式（b*c）的右括号，如果把操作符*移到右括号处，替代他，然后删去左括号，得到bc*，即可把这个子表达式转化为后缀表达式。同理。将操作符替代左括号，即可得到前缀表达式*bc。

通过的中缀转后缀算法：

• 中缀表达式转化为后缀的处理过程中，操作符要比操作数后输出，所以在扫描到第二个操作数之前，需要把操作符保存起来。
• 而这些暂存的寄存符，也需要反转次序来输出，所以我们使用栈来实现。
• 栈顶的操作符就是最近暂存进去的，当遇到一个新的操作符之后，就需要跟栈顶的操作符比较一下优先级，再行处理。
  
  
  

from Stack import Stack

def swift(oldstring):
    newlist = []
    oldstring = ""
    tokenlist = oldstring.split()
    opstack = Stack()
    # 定义一个操作符优先字典
    dict = {}
    dict['+'] = 1
    dict['-'] = 1
    dict['*'] = 2
    dict['/'] = 2
    dict['('] = 3


    for token in tokenlist:
        if token in '1234567890' or token in 'ABCDEFGJIJKLMNOPQRSTUVWXYZ':
           newlist.append(token)
        elif token == '(':
            opstack.push(token)
        elif token == ')':
            toptoken = opstack.pop()
            while toptoken != '(':   #反复弹出栈顶操作符，加入输出列表末尾，直至遇到(
                newlist.append(toptoken)
                toptoken = opstack.pop()
        else:
            while (not opstack.is_empty()) and (dict[opstack.peek()] >= dict[token]):
                newlist.append(opstack.pop())
            opstack.push(token)         #注意这条语句的缩进


    while not opstack.is_empty():
        newlist.append(opstack.pop())

    return "".join(newlist)


print(swift("A+B*C"))

队列抽象数据类型以及Python实现

1. 这种次序安排的原则：先进先出，仅有一个入口和一个出口。
2. 计算机中队列的例子：打印队列、操作系统底层中的进程调度、键盘缓冲
   
   
3. 队列操作定义：
   
   
   用列表来容纳队列数据线

class Queue(object):
    def __init__(self):
        self.queue = []
    def isEmpty(self):
        return  len(self.queue) == 0
    def enqueue(self,element):
        self.queue.insert(0,element)
    def dequeue(self):
        return self.queue.pop()
    def size(self):
        return len(self.queue)

队列的应用：热土豆问题

class Queue:
    def __init__(self):
        self.queue = []
    def enqueue(self,item):
        self.queue.insert(0,item)
    def size(self):
        return len(self.queue)
    def dequeue(self):
        return self.queue.pop()

def potato(namelist,num):
    q = Queue()
    for name in namelist:
        q.enqueue(name)
    while q.size() > 1:
        for i in range(num):
            q.enqueue(q.dequeue())  #进行一次传递
        q.dequeue()
    return q.dequeue()

print(potato(["Bill","David","Susan","Jane","kent","Brad"],7))

队列的应用：打印队列

在能够接受的等待时间范围内，系统能容纳多少用户以多高频率提交多少打印任务？

实例配置：一个实验室，在任意的一个小时内，大约有10名学生在场，这一小时中，每人会发起2次左右的打印，每次1～20页。打印机的性能是：以草稿模式打印的话，每分钟10页，以正常模式打印的话，打印质量好，但速度下降为每分钟5页。
问题建模：
打印任务的属性：提交时间、打印页数
打印队列的属性：具有FIFO性质的打印任务队列
打印机的属性：打印速度、是否忙
过程：实施打印
当前的打印作业：正在打印的作业
打印结束倒计时：新作业开始打印时开始倒计时，回0表示打印完毕，可以处理下一个作业

代码：

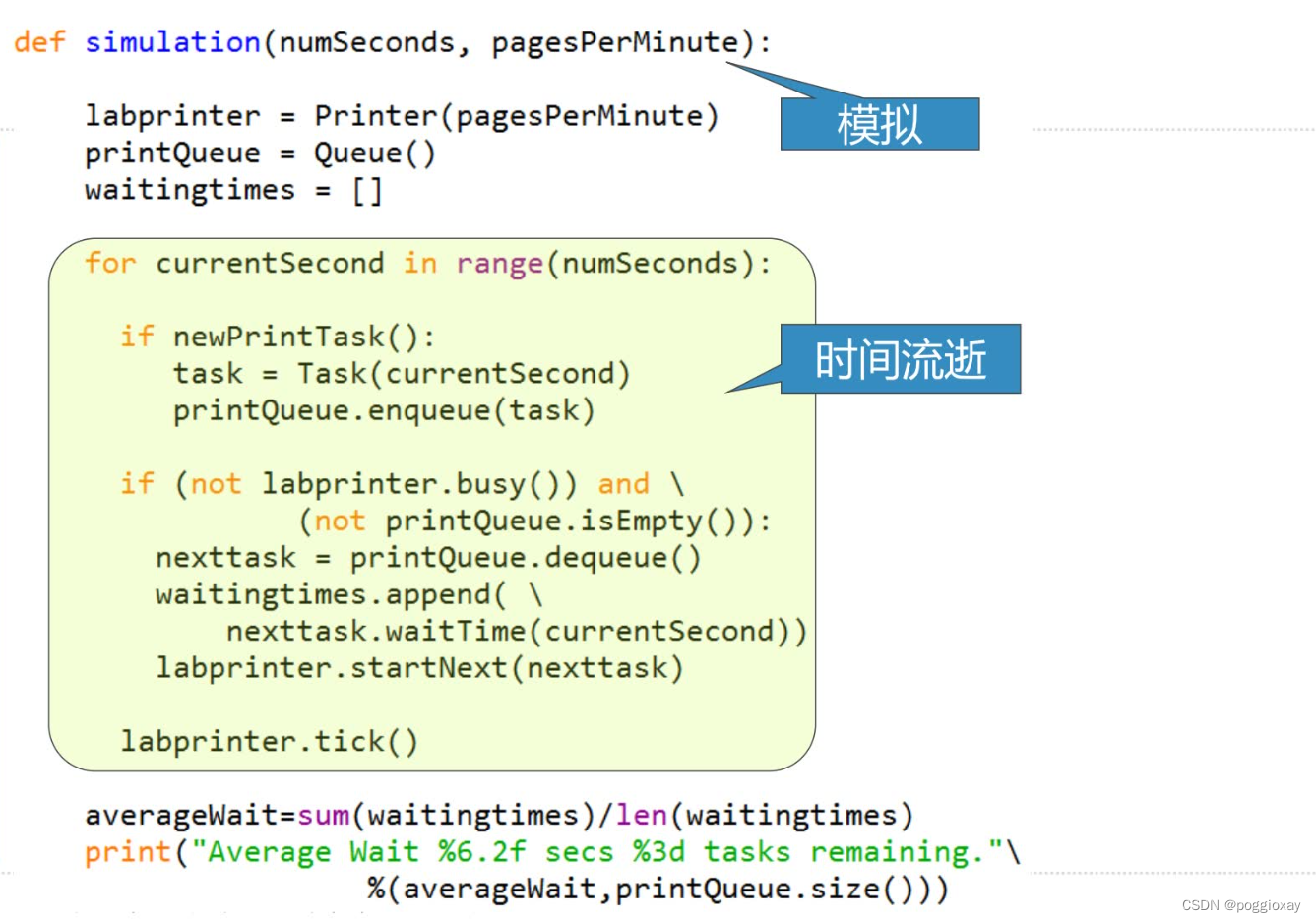
双端队列抽象数据类型以及Python实现

双端队列Deque是一种有次序的数据集,跟队列相似，其两端可以称作“首”“尾”端，但deque中数据项既可以从队首加入，也可以从队尾加入;数据项也可以从两端移除。某种意义上说，双端队列集成了栈和队列的能力。

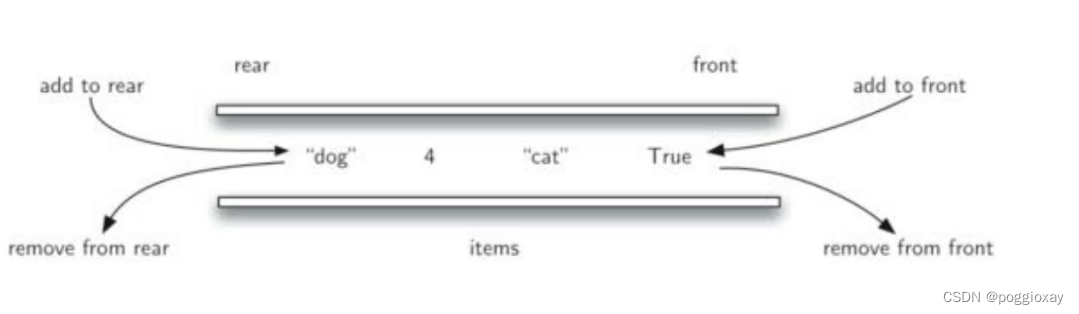
Python实现双端队列

采用List实现：List下标0作为deque的尾端，List下标-1作为deque的首端。

class Deque:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items ==[]
    def addFront(self, item) :
        self.items.append(item)
    def addRear(self, item) :
        self.items.insert(0,item)
    def removeFront(self):
        return self.items.pop()
    def removeRear(self,item):
        return self.items.pop(0)
    def size(self):
        return len(self.items)

应用：回文词判定

先将需要判定的词从队尾加入deque，再从两端同时移除字符判定是否相同，直到deque中剩下0个或1个字符。

#radar
from Deque import Deque
def check(String):
    deque = Deque()
    for i in String:
        deque.addRear(i)
    stillequal = True
    while deque.size() > 1 and stillequal:
        first = deque.removeFront()
        last = deque.removeRear()
        if first != last:
            stillequal = False
            break
        else:
            stillequal = True
    return stillequal

print(check("radar"))

无序表抽象数据类型以及Python实现

无序表：按照数据项的位置进行存放，对内容没有。如考试成绩 [54，23，78]

采用链表实现无序表

为了实现无序表数据结构，可以采用链接表的方案。虽然列表数据结构要求保持数据项的前后相对位置，但这种前后位置的保持，并不要求数据项依次存放在连续的存储空间。


链表实现的最基本元素是节点Node。每个节点至少要包含2个信息:数据项本身，以及指向下一个节点的引用信息。
注意： next为None的意义是没有下一个节点了，这个很重要。

class Node:
    def __init__(self,initdata):
        self.data = initdata
        self.next = None
    def getData(self):
        return self.data
    def getNext(self):
        return self.next
    def setData(self,newdata):
        self.data = newdata
    def setNext(self,newnext):
        self.next = newnext

可以采用链接节点的方式构建数据集来实现无序表。链表的第一个和最后一个节点最重要如果想访问到链表中的所有节点，就必须从第一个节点开始沿着链接遍历下去。
所以无序表必须要有对第一个节点的引用信息，设立一个属性head，保存对第一个节点的引用空表的head为None。

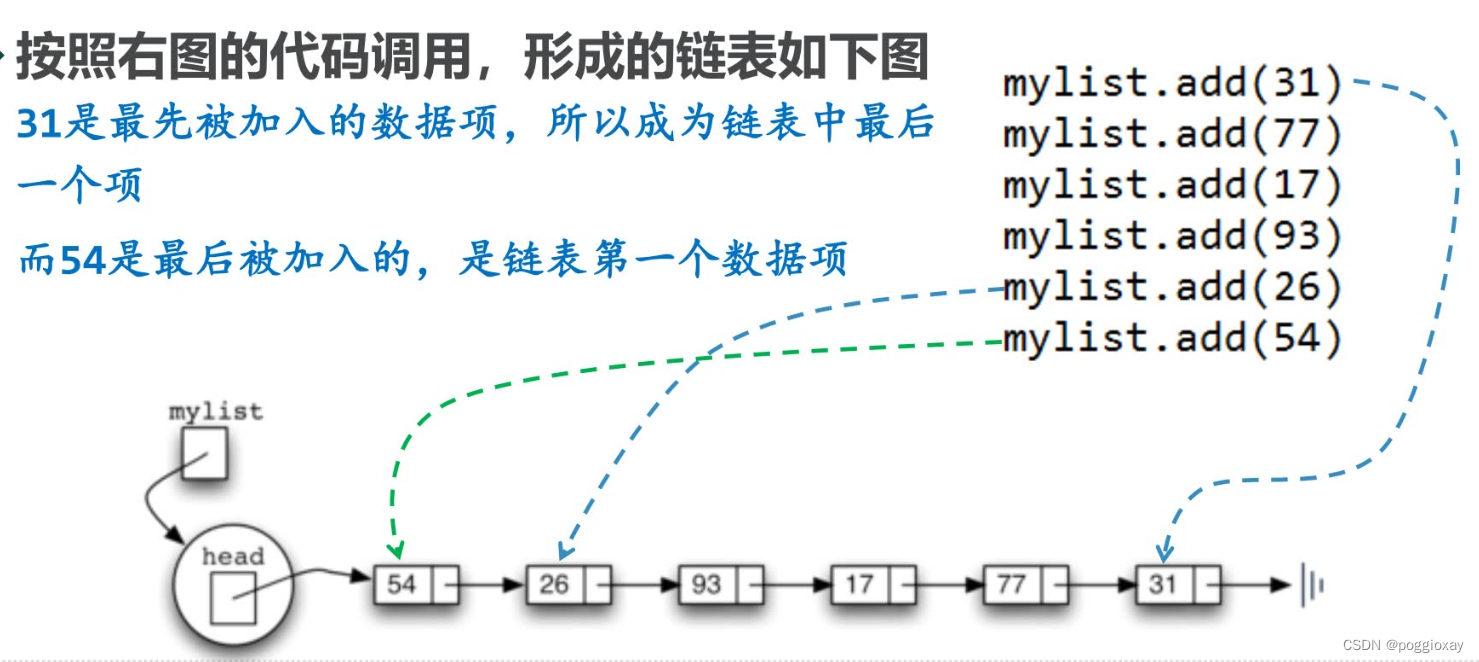
随着数据项的加入，无序表的head始终指向链条中的第一个节点。

注意： 无序表mylist对象本身并不包含数据项【数据项在节点中】，其中包含的head只是对首个节点Node的引用，判断空表的isEmpty()很容易实现。

add()方法

由于无序表并没有限定数据项之间的顺序，新数据项可以加入到原表的任何位置按照实现的性能考虑，应添加到最容易加入的位置上。

由链表结构我们知道要访问到整条链上的所有数据项，都必须从表头head开始沿着next链接逐个向后查找，所以添加新数据项最快捷的位置是表头，整个链表的首位置。

size()方法

search()方法

remove(item)方法

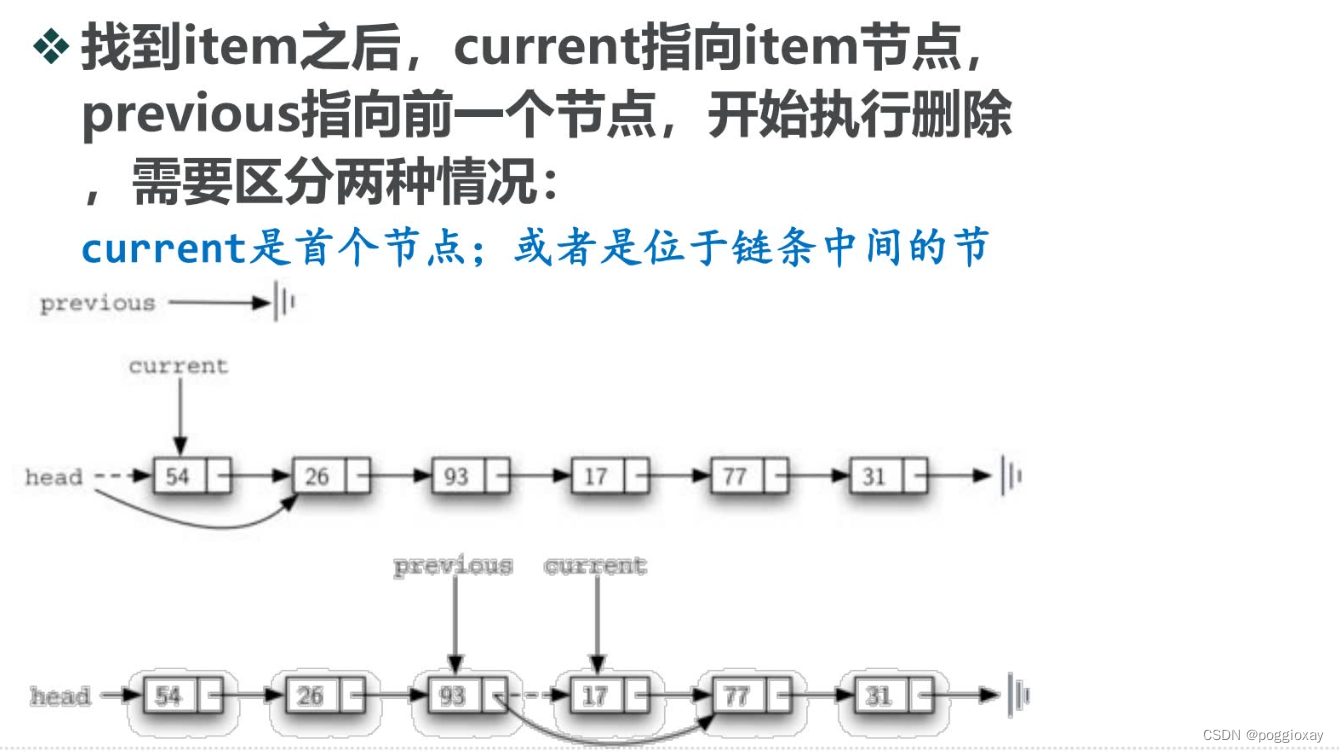
def remove(self,item):
    current = self.head
    previous = None
    found = False
    while not found:
        if current.getData() == item:
            found = True
        else:
            previous = current
            current = current.getNext()
    if previous == None:
        self.head = current.getNext()
    else:
        previous.setNext(current.getNext())

有序表抽象数据类型及Python实现

有序表是一种数据项依照其某可比性质【如整数大小、字母表先后】来决定在列表中的位置，越“小"的数据项越靠近列表的头，越靠“前”。

在实现有序表的时候，需要记住的是，数据项的相对位置,取决于它们之间的“大小”比较。由于Python的扩展性，下面对数据项的讨论并不仅适用于整数，可适用于所有定义了_gt_方法【即’>'操作符】的数据类型。

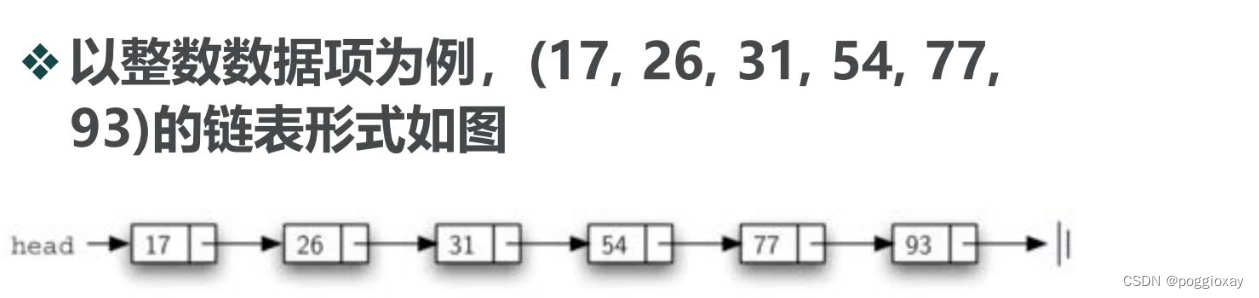
同样采用链表方法实现，Node定义相同，有序表也设置一个head来保存链表表头的引用。

class OrderedList:
	def __init__(self):
		self.head = None

对于isEmpty/size/remove这些方法，与节点的次序无关，所以其实现跟无序表是一样的。search/add方法则需要有修改。

serch()方法

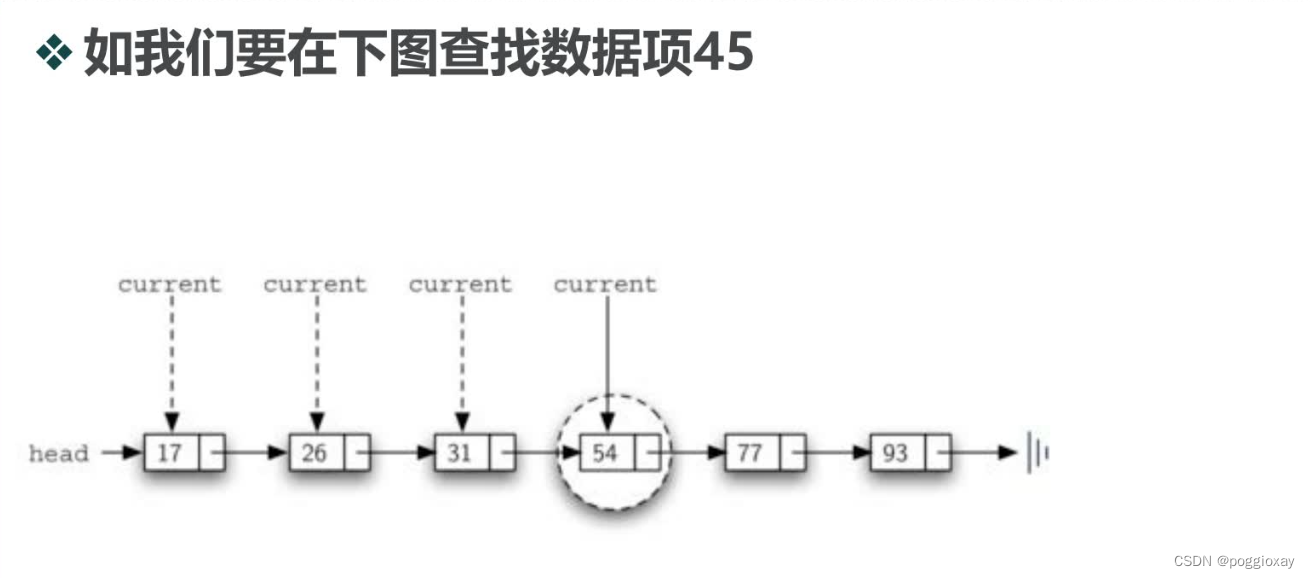
def search(self,item):
    current = self.head
    found = False
    stop = False
    while current != None and not found and not stop:
        if current.getData() == item:
            found = True
        else:
            if current.getData() > item:
                stop = True
            else:
                current = current.getNext()
    return  found

add()方法

相比无序表，改变最大的方法是add，因为add方法必须保证加入的数据项添加在合适的位置，以维护整个链表的有序性比如在(17，26，54,77,93)的有序表中，加入数据项31，我们需要沿着链表，找到第一个比31大的数据项54，将31插入到54的前面。

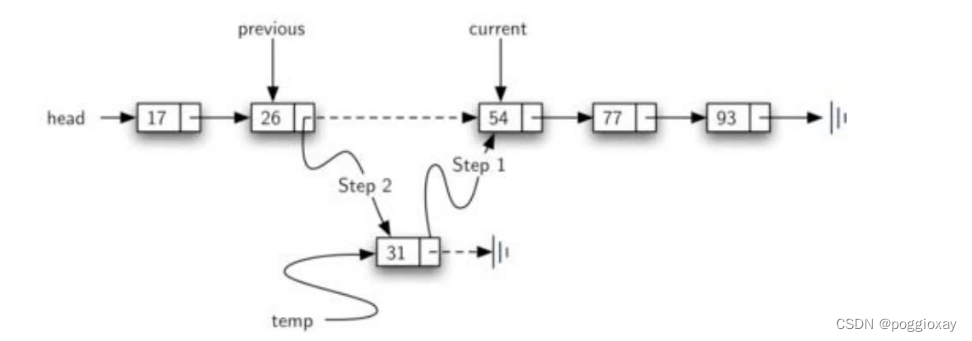
由于涉及到的插入位置是当前节点之前，而链表无法得到“前驱”节点的引用。所以要跟remove方法类似，引入previous的引用，跟随当前节点current，一旦找到首个比31大的数据项，previous就派上用场了。

链表实现的算法分析

1. 对于链表复杂度的分析，主要是看相应的方法是否涉及到链表的遍历。
2. 对于一个包含节点数为n的链表，isEmpty是o(1)，因为仅需要检查head是否为None.
3. size是o(n)，因为除了遍历到表尾，没有其它办法得知节点的数量
4. search/remove以及有序表的add方法，则是o(n),因为涉及到链表的遍历，按照概率其平均操作的次数是n/2nxi
5. 无序表的add方法是O(1)，因为仅需要插入到表头。
6. 链表实现的List，跟Python内置的列表数据类型，在有些相同方法的实现上的时间复杂度不同，主要是因为Python内置的列表数据类型是基于顺序存储来实现的，并进行了优化。

线性结构小结

1. 线性数据结构将数据项以某种线性的次序组织起来。
2. 栈Stack维持了数据项后进先出LIFO的次序，stack的基本操作包括push, pop,isEmpty。
3. 队列Queue维持了数据项先进先出FIFO的次序，queue的基本操作包括enqueue,dequeue,isEmpty。
4. 书写表达式的方法有前缀、中缀和后缀三种，由于栈结构具有次序反转的特性，所以栈结构适合用于开发表达式求值和转换的算法。
5. “模拟系统”可以通过一个对现实世界问题进行抽象建模，并加入随机数动态运行，为复杂问题的决策提供各种情况的参考，队列queue可以用来进行模拟系统的开发。
6. 双端队列Deque可以同时具备栈和队列的功能，deque的主要操作包括addFront,addRear,removeFront,removeRear，isEmpty 。
7. 列表List是数据项能够维持相对位置的数据集，链表的实现，可以保持列表维持相对位置的特点，而不需要连续的存储空间。链表实现时，其各种方法，对链表头部head需要特别的处理。