3.1 柱状图
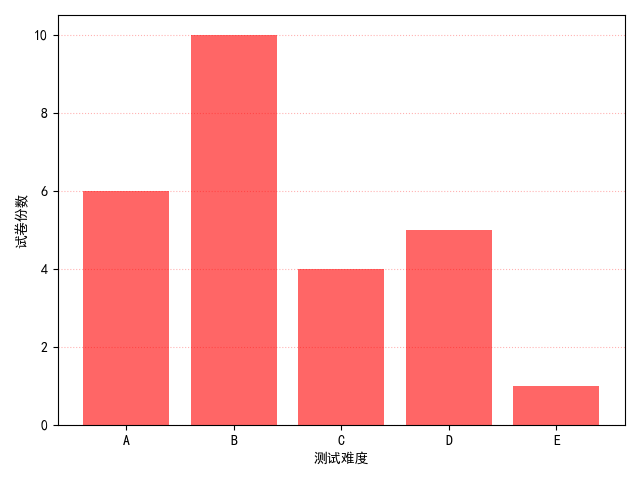
以 Python 代码的形式讲解柱状图的绘制原理,这里重点讲解 bar()函数的使用方法。
代码:
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
# some simple data
x = [1,2,3,4,5]
y = [6,10,4,5,1]
# create bar
plt.bar(x,y,align="center",color="r",tick_label=["A","B","C","D","E"],alpha=0.6)
# set x,y_axis label
plt.xlabel("测试难度")
plt.ylabel("试卷份数")
# set yaxis grid
plt.grid(True,axis="y",ls=":",color="r",alpha=0.3)
plt.show()运行结果:
为了展示图表里的中文字体,我们选择字体“SimHei”, 通 过 “mpl.rcParams["font.sans-serif"]
=["SimHei"]”完成字体配置任务。不使用默认的“Unicode minus”模式来处理坐标轴轴线的刻度标
签是负数的情况,一般可以使用“ASCII hyphen”模式来处理坐标轴轴线的负刻度值的情况,即 通
过“mpl.rcParams["axes.unicode_minus"]=False”语句实现模式的选择。
语句中各参数的含义:
x:柱状图中的柱体标签值。
y:柱状图中的柱体高度。
align:柱体对齐方式。
color:柱体颜色。
tick_label:刻度标签值。
alpha:柱体的透明度。
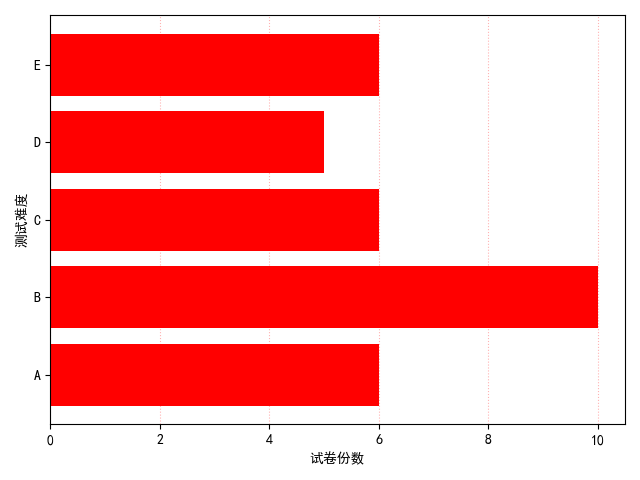
3.2 条形图
将柱状图中的柱体由垂直方 向变成水平方 向,柱状图就变成条形图,函数也就变成barh(x,y,align="center",color="k",tick_label=["A","B","C","D","E"]),其中参数 x 是 y 轴上柱体标签值,y 是柱体的宽度,在 x 轴上显示,tick_label 表示 y 轴上的柱体标签值。
代码:
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
# some simple data
x = [1,2,3,4,5]
y = [6,10,6,5,6]
# create horizontal bar
plt.barh(x,y,align="center",color="r",tick_label=["A","B","C","D","E"])
# set x,y_axis label
plt.ylabel("测试难度")
plt.xlabel("试卷份数")
# set xaxis grid
plt.grid(True,axis="x",ls=":",color="r",alpha=0.3)
plt.show()运行结果:
3.3 堆积图
堆积图顾名思义就是将若干统计图形堆叠起来的统计图形,自然是一种组合式图形。下面,我们就结合前面讲过的柱状图和条形图的绘制方法,具体讲解堆积柱状图和堆积条形图的实现方法。
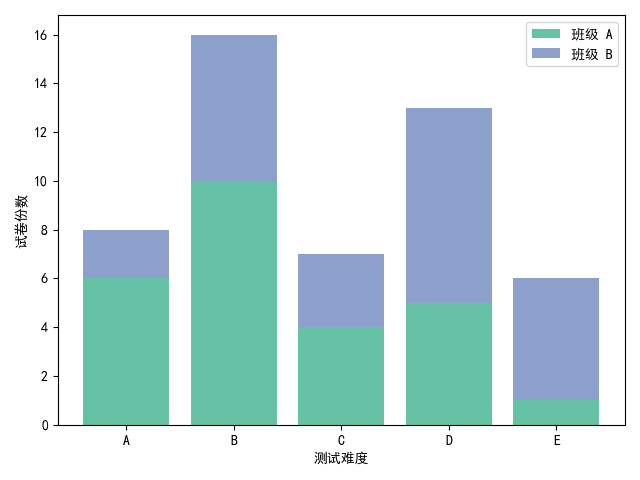
3.3.1堆积柱状图
如果将函数 bar()中的参数 bottom 的取值设定为列表 y,列表 y1=[2,6,3,8,5]代表另一套试卷的份
数,函数 bar(x,y1,bottom=y,color="r")就会输出堆积柱状图。
代码:
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
# some simple data
x = [1,2,3,4,5]
y = [6,10,4,5,1]
y1 = [2,6,3,8,5]
# create bar
plt.bar(x,y,align="center",color="#66c2a5",tick_label=["A","B","C","D","E"],label="班级 A")
plt.bar(x,y1,align="center",bottom=y,color="#8da0cb",label="班级 B")
# set x,y_axis label
plt.xlabel("测试难度")
plt.ylabel("试卷份数")
plt.legend()
plt.show()运行结果:
3.3.2堆积条形图
将函数 barh()中的参数 left 的取值设定为列表 y,列表 y1=[2,6,3,8,5]代表另一套试卷的份数,
函数 barh(x,y1,left=y,color="r")就会输出堆积条形图。
代码:
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
# some simple data
x = [1,2,3,4,5]
y = [6,10,4,5,1]
y1 = [2,6,3,8,5]
# create bar
plt.barh(x,y,align="center",color="#66c2a5",tick_label=["A","B","C","D","E"],label="班级 A")
plt.barh(x,y1,align="center",left=y,color="#8da0cb",label="班级 B")
# set x,y_axis label
plt.xlabel("测试难度")
plt.ylabel("试卷份数")
plt.legend()
plt.show()运行结果:
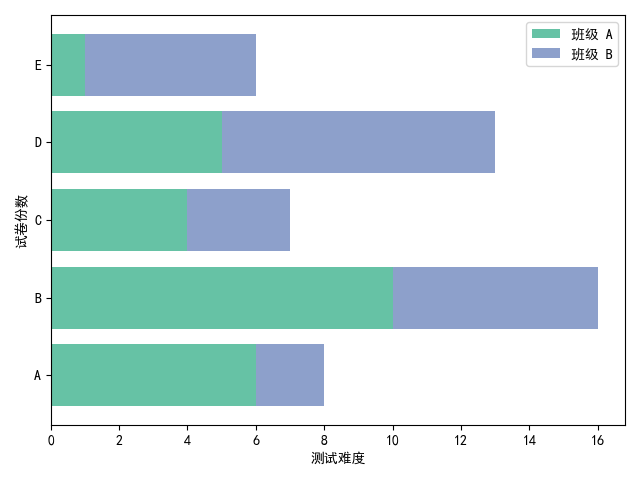
3.4 分块图
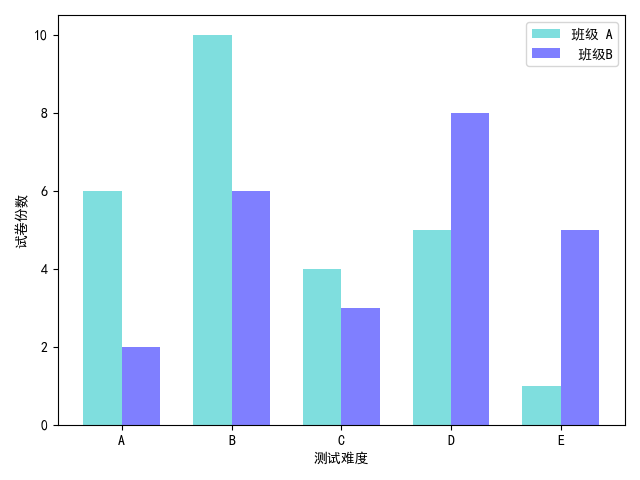
3.4.1多数据并列柱状图
对于堆积柱状图而言,我们也可以选择多数据并列柱状图来改变堆积柱状图的可视化效果。当
然,堆积条形图也可以改变可视化效果,呈现多数据平行条形图的图形样式。
代码:
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
# some simple data
x = np.arange(5)
y = [6,10,4,5,1]
y1 = [2,6,3,8,5]
bar_width = 0.35
tick_label=["A","B","C","D","E"]
# create bar
plt.bar(x,y,bar_width,color="c",align="center",label="班级 A",alpha=0.5)
plt.bar(x+bar_width,y1,bar_width,color="b",align="center",label=" 班级B",alpha=0.5)
# set x,y_axis label
plt.xlabel("测试难度")
plt.ylabel("试卷份数")
# set xaxis ticks and ticklabels
plt.xticks(x+bar_width/2,tick_label)
plt.legend()
plt.show()运行结果:
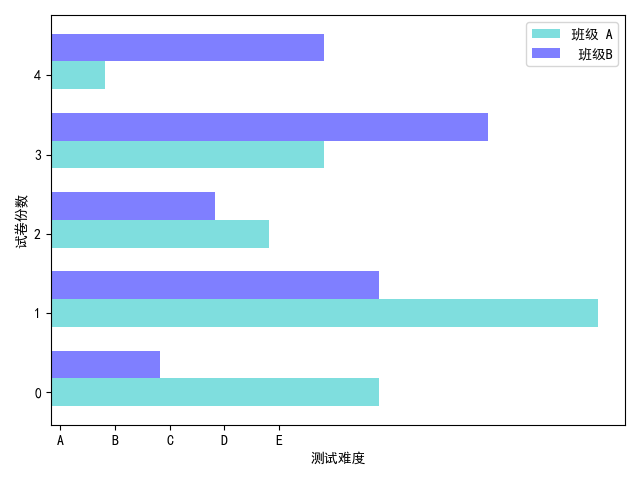
3.4.2多数据平行条形图
对于堆积条形图而言,我们也同样可以选择多数据平行条形图来改变堆积条形图的可视化效果。
多数据平行条形图与多数据并列柱状图的实现方法是类似的,只是调用函数由 bar()变成 barh()。
代码:
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
# some simple data
x = np.arange(5)
y = [6,10,4,5,1]
y1 = [2,6,3,8,5]
bar_width = 0.35
tick_label=["A","B","C","D","E"]
# create bar
plt.barh(x,y,bar_width,color="c",align="center",label="班级 A",alpha=0.5)
plt.barh(x+bar_width,y1,bar_width,color="b",align="center",label=" 班级B",alpha=0.5)
# set x,y_axis label
plt.xlabel("测试难度")
plt.ylabel("试卷份数")运行结果:
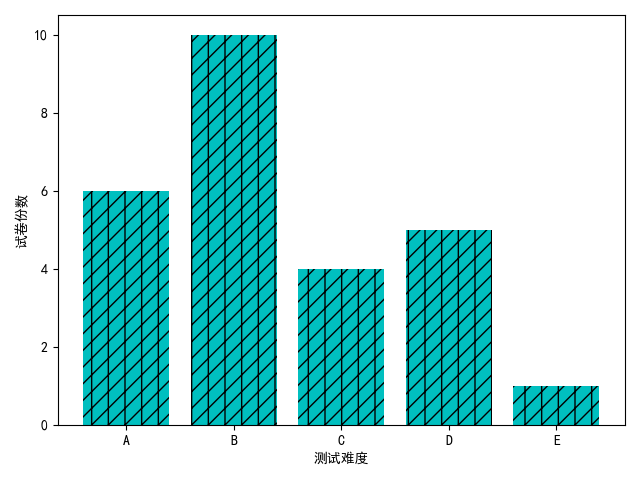
3.5 参数探索
如果想在柱体上绘制装饰线或装饰图,也就是说,设置柱体的填充样式。我们可以使用关 键字参数hatch,关键字参数 hatch 可以有很多取值,例如,“"/"”“"\\"”“"|"”“"-"”等,每种符号字符串
都是一种填充柱体的几何样式。而且,符号字符串的符号数量越多,柱体的几何图形的密集程度越高。
代码:
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
# some simple data
x = [1,2,3,4,5]
y = [6,10,4,5,1]
# create bar
plt.bar(x,y,align="center",color="c",tick_label=["A","B","C","D","E"],hatch="|//")
# set x,y_axis label
plt.xlabel("测试难度")
plt.ylabel("试卷份数")
plt.show()运行结果:
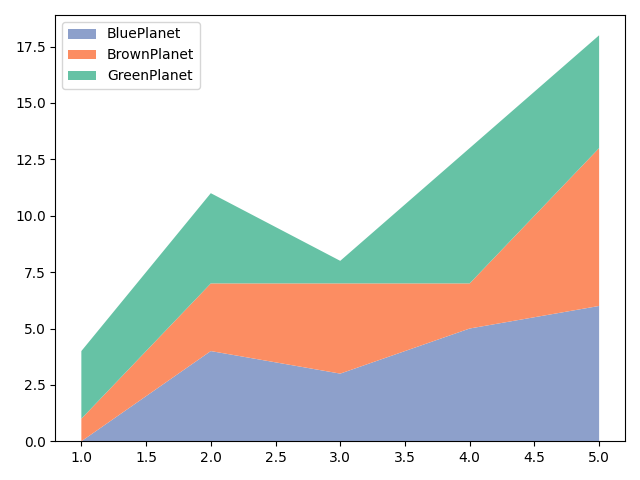
3.6 堆积折线图、间断条形图和阶梯图
3.6.1用函数 stackplot()绘制堆积折线图
堆积折线图是通过绘制不同数据集的折线图而生成的。堆积折线图是按照垂直方向上彼此堆叠
且又不相互覆盖的排列顺序,绘制若干条折线图而形成的组合图形。
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(1,6,1)
y = [0,4,3,5,6]
y1 = [1,3,4,2,7]
y2 = [3,4,1,6,5]
labels = ["BluePlanet","BrownPlanet","GreenPlanet"]
colors = ["#8da0cb","#fc8d62","#66c2a5"]
plt.stackplot(x,y,y1,y2,labels=labels,colors=colors)
plt.legend(loc="upper left")
plt.show()运行如图:
3.6.2用函数 broken_barh ()绘制间断条形图
间断条形图是在条形图的基础上绘制而成的,主要用来可视化定性数据的相同指标在时间维度
上的指标值的变化情况,实现定性数据的相同指标的变化情况的有效直观比较。
代码如下:
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
mpl.rcParams["font.sans-serif"]=["LiSu"]
mpl.rcParams["axes.unicode_minus"]=False
plt.broken_barh([(30,100),(180,50),(260,70)],(20,8),facecolors="#1f78b4")
plt.broken_barh([(60,90),(190,20),(230,30),(280,60)],(10,8),facecolors=(
"#7fc97f","#beaed4","#fdc086","#ffff99"))
plt.xlim(0,360)
plt.ylim(5,35)
plt.xlabel("演出时间")
plt.xticks(np.arange(0,361,60))
plt.yticks([15,25],["歌剧院 A","歌剧院 B"])
plt.grid(ls="-",lw=1,color="gray")
plt.title("不同地区的歌剧院的演出时间比较")
plt.show()运行如下:
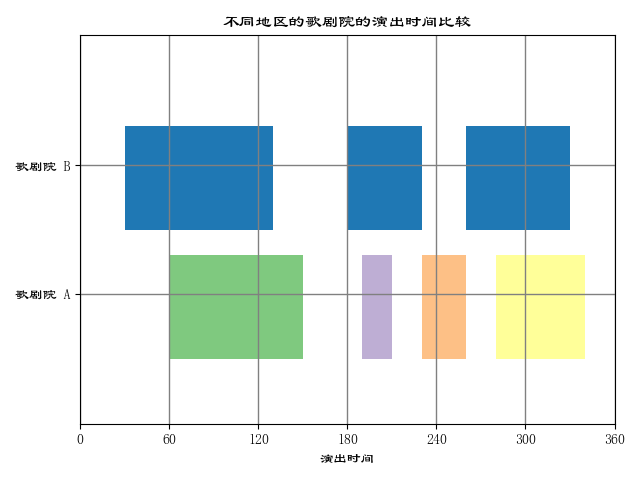
列表“[(60,90),(190,20),(230,30),(280,60)]”的元组表示从起点是 x 轴的数值为 60 的位置起,沿x轴正方向移动 90 个单位。其他元组的含义类似。参数“(10,8)”表示从起点是 y 轴的数值为 10 的位置起,沿 y 轴正方向移动 8 个单位,这就是每个柱体的高度和垂直起始位置。关键字参数 facecolors 表示每个柱体的填充颜色,这里使用 HEX 模式的颜色表示方法。
3.6.3用函数 step()绘制阶梯图
阶梯图在可视化效果上正如图形的名字那样形象,就如同山间的台阶时而上升时而下降,从图形本身而言,很像折线图。也用采是反映数据的趋势变化或是周期规律的。阶梯图经常使用在时间序列数据的可视化任务中,凸显时序数据的波动周期和规律。
代码实现
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(1,10,10)
y = np.sin(x)
plt.step(x,y,color="#8dd3c7", where="pre",lw=2)
plt.xlim(0,11)
plt.xticks(np.arange(1,11,1))
plt.ylim(-1.2,1.2)
plt.show()运行结果如下:
3.7 直方图
直方图是用来展现连续型数据分布特征的统计图形。利用直方图我们可以直观地分析出数据的
集中趋势和波动情况。
我们以 Python 代码的形式讲解直方图的绘制原理,主要讲解 hist()函数的使用方法。
代码实现
import matplotlib as mpl
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
import matplotlib.pyplot as plt
import numpy as np
# set test scores
scoresT = np.random.randint(0,100,100)
x = scoresT
# plot histogram
bins = range(0,101,10)
plt.hist(x,bins=bins,
color="#377eb8",
histtype="bar",
rwidth=10)
# set x,y-axis label
plt.xlabel("测试成绩")
plt.ylabel("学生人数")
plt.show()运行结果如下:
首先,我们先解释一下函数 hist(x,bins=bins,color= "b",histtype="bar",label="score",rwidth=10)的参数的含义。
x:连续型数据输入值。
bins:用于确定柱体的个数或是柱体边缘范围。
color:柱体的颜色。
histtype:柱体类型。
label:图例内容。
rwidth:柱体宽度。
3.8 饼图
饼图是用来展示定性数据比例分布特征的统计图形。通过绘制饼图,我们可以清楚地观察出数
据的占比情况。
我们以 Python 代码的形式来讲述饼图的绘制原理,我们重点讲解 pie()函数的使用细节。
代码实现:
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
labels = "A 难度水平","B 难度水平","C 难度水平","D 难度水平"
students = [0.35,0.15,0.20,0.30]
colors = ["#377eb8","#4daf4a","#984ea3","#ff7f00"]
explode = (0.1,0.1,0.1,0.1)
# exploded pie chart
plt.pie(students,explode=explode,
labels=labels,
autopct="%3.1f%%",
startangle=45,
shadow=True,
colors=colors)
plt.title("选择不同难度测试试卷的学生百分比")
plt.show()运行结果如图:
解释一下函 数 pie(students,explode=explode,labels=labels,autopct= "%3.1f%%",
startangle=45,shadow=True, colors=colors)的参数含义,如下所示。
students:饼片代表的百分比。
explode:饼片边缘偏离半径的百分比。
labels:标记每份饼片的文本标签内容。
autopct:饼片文本标签内容对应的数值百分比样式。
startangle:从 x 轴作为起始位置,第一个饼片逆时针旋转的角度。
shadow:是否绘制饼片的阴影。
colors:饼片的颜色。
上面讲过分裂式饼图的绘制方法,接下来就调整函数 pie()的参数,绘制其他类型的饼图。
如果我们不绘制分裂式饼图 ,那么只需要去掉参数 explode 即可。
代码:
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
labels = "A 难度水平","B 难度水平","C 难度水平","D 难度水平"
students = [0.35,0.15,0.20,0.30]
colors = ["#377eb8","#4daf4a","#984ea3","#ff7f00"]
# exploded pie chart
plt.pie(students,
labels=labels,
autopct="%3.1f%%",
startangle=45,
pctdistance=0.7,
labeldistance=1.2,
colors=colors)
plt.title("选择不同难度测试试卷的学生百分比")
plt.show()运行结果:
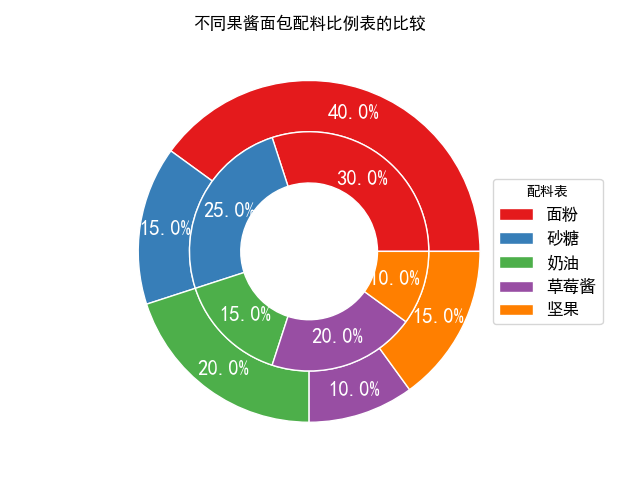
饼图不仅可以用来描述定性数据的比例分布,还可以将多个饼图进行嵌套,从而实现内嵌环形
饼图的可视化效果。
代码:
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
mpl.rcParams["font.sans-serif"]=["SimHei"]
mpl.rcParams["axes.unicode_minus"]=False
elements = ["面粉","砂糖","奶油","草莓酱","坚果"]
weight1 = [40,15,20,10,15]
weight2 = [30,25,15,20,10]
colormapList = ["#e41a1c","#377eb8","#4daf4a","#984ea3","#ff7f00"]
outer_colors = colormapList
inner_colors = colormapList
wedges1,texts1,autotexts1 = plt.pie(weight1,
autopct="%3.1f%%",
radius=1,
pctdistance=0.85,
colors=outer_colors,
textprops=dict(color="w"),
wedgeprops=dict(width=0.3,edgecolor="w"))
wedges2,texts2,autotexts2 = plt.pie(weight2,
autopct="%3.1f%%",
radius=0.7,
pctdistance=0.75,
colors=inner_colors,
textprops=dict(color="w"),
wedgeprops=dict(width=0.3,edgecolor="w"))
plt.legend(wedges1,
elements,
fontsize=12,
title="配料表",
loc="center left",
bbox_to_anchor=(0.91, 0, 0.3, 1))
plt.setp(autotexts1,size=15,weight="bold")
plt.setp(autotexts2,size=15,weight="bold")
plt.setp(texts1,size=12)
plt.title("不同果酱面包配料比例表的比较")
plt.show()运行结果:
3.9误差棒图
在很多科学实验中都存在测量误差或是试验误差,这是无法控制的客观因素。这样,在可视化试验结果的时候,最好可以给试验结果增加观测结果的误差以表示客观存在的测量偏差。误差棒图就是可以运用在这一场景中的很理想的统计图形。通过抽样获得样本,对总体参数进行估计会由于样本的随机性导致参数估计值出现波动,因此需要用误差置信区间来表示对总体参数估计的可靠范围。误差棒就可以很好地实现充当总体参数估计的置信区间的角色。误差棒的计算方法可以有很多种:单一数值、置信区间、标准差和标准误等。误差 棒的可视化展示效果也有很多种样式:水平误差棒、垂直误差棒、对称误差棒和非对称误差棒等。
我们以 Python 代码的形式讲解误差棒的绘制原理,主要讲解函数 errorbar()的使用方法和参数使用细节。
代码实现
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0.1,0.6,10)
y = np.exp(x)
error = 0.05+0.15*x
lower_error = error
upper_error = 0.3*error
error_limit = [lower_error,upper_error]
plt.errorbar(x,y,yerr=error_limit,fmt=":o",
ecolor="y",elinewidth=4,
ms=5,mfc="c",mec='r',
capthick=1,capsize=2)
plt.xlim(0,0.7)
plt.show()运行结果如下:
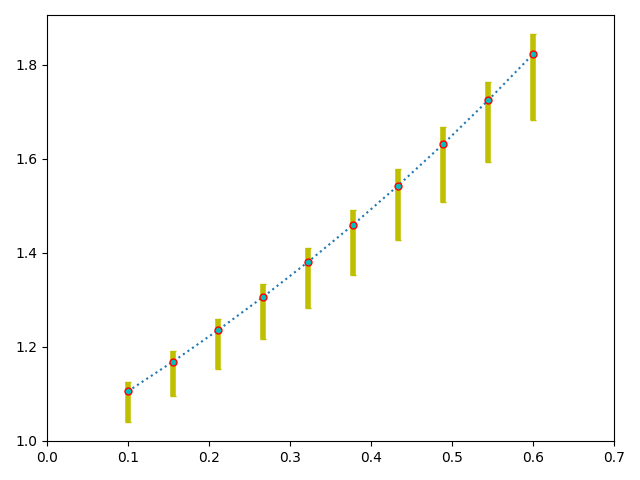
我们采用单一数值的非对称形式的误差棒,函数 errorbar()的参数含义如下所示。
x,y:数据点的位置。
yerr:单一数值的非对称形式误差范围。
fmt:数据点的标记样式和数据点标记的连接线样式。
ecolor:误差棒的线条颜色。
elinewidth:误差棒的线条粗细。
ms:数据点的大小。
mfc:数据点的标记颜色。
mec:数据点的标记边缘颜色。
capthick:误差棒边界横杠的厚度。
capsize:误差棒边界横杠的大小。
函数 errorbar()里的关键字参数 yerr 使用了误差范围的非对称形式,而且是数据点下方的误差范围大于数据点上方的误差范围。关键字参数 xerr 也可以使用类似的误差范围,关键字参数 fmt 如果取“none”值时,数据点的连线、数据点的标记样式和颜色都不显示。关键字参数 capthick 也可以用关键字参数 mew 代替。
本节我们讲解了误差棒图的绘制方法,知道了误差棒图是用来展示定量数据误差范围的统计图形。如果只是单一地使用误差棒图可能不会很好地发挥这种统计图形的实际应用价值。因此,需要我们将其他统计图形与误差棒图相结合来展示数据集的测量误差等内容。
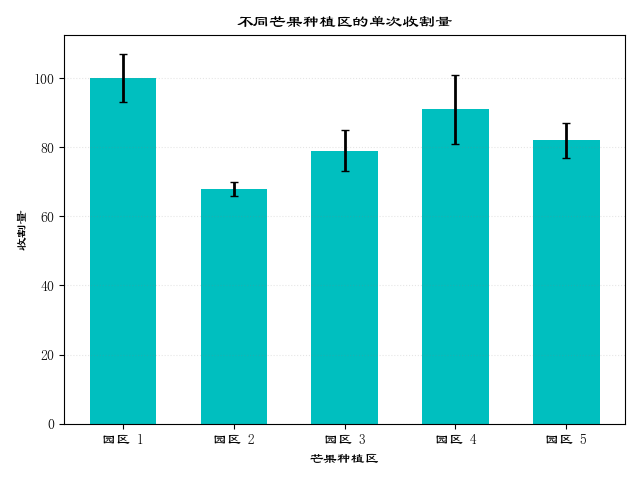
带误差棒的柱状图
我们前面已经讲过柱状图和误差棒图的绘制原理,现在我们可以将这两种统计图形结合起来,绘制带误差棒的柱状图,使得统计图形在反映数据测量误差方面的应用领域得到拓展。这种统计图形在科学研究领域里应用范围很广泛。
(1)代码实现
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
mpl.rcParams["font.sans-serif"]=["LiSu"]
mpl.rcParams["axes.unicode_minus"]=False
# some simple data
x = np.arange(5)
y = [100,68,79,91,82]
std_err = [7,2,6,10,5]
error_attri = dict(elinewidth=2,ecolor="black",capsize=3)
# create bar with errorbar
plt.bar(x,y,
color="c",
width=0.6,
align="center",
yerr=std_err,
error_kw=error_attri,
tick_label=["园区 1","园区 2","园区 3","园区 4","园区 5"])
# set x,y_axis label
plt.xlabel("芒果种植区")
plt.ylabel("收割量")
# set title of axes
plt.title("不同芒果种植区的单次收割量")
# set yaxis grid
plt.grid(True,axis="y",ls=":",color="gray",alpha=0.2)
plt.show()运行结果如下:
带误差棒的条形图
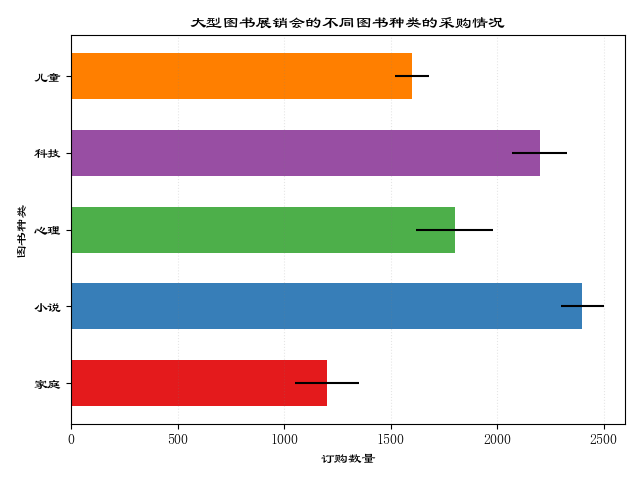
我们前面已经讲过条形图和误差棒图的绘制原理,现在我们可以将这两种统计图形结合起来,绘制带误差棒的条形图。如果我们试图反映定性数据的分布特征,同时还要反映分布的波动特征,那么这种统计图形就是合适之选。这种统计图形在科学研究领域里的用途很多。
代码实现
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
mpl.rcParams["font.sans-serif"]=["LiSu"]
mpl.rcParams["axes.unicode_minus"]=False
# some simple data
x = np.arange(5)
y = [1200,2400,1800,2200,1600]
std_err = [150,100,180,130,80]
bar_width = 0.6
colors = ["#e41a1c","#377eb8","#4daf4a","#984ea3","#ff7f00"]
# create horizontal bar
plt.barh(x,y,
bar_width,
color=colors,
align="center",
xerr=std_err,
tick_label=["家庭","小说","心理","科技","儿童"])
# set x,y_axis label
plt.xlabel("订购数量")
plt.ylabel("图书种类")
# set title
plt.title("大型图书展销会的不同图书种类的采购情况")
# set xaxis grid
plt.grid(True,axis="x",ls=":",color="gray",alpha=0.2)
plt.xlim(0,2600)
plt.show()运行结果如下:
带误差棒的条形图的绘制是通过使用函数 barh()中的关键字参数 xerr 实现的。其他关键字参数的含义和用法都已经在前面有关柱状图里绘制条形图的部分详细介绍过。条形图的填充颜色是使用HEX 模式进行命名的,文中的中文字体是使用隶书“LiSu”字体。
带误差棒的多数据并列柱状图
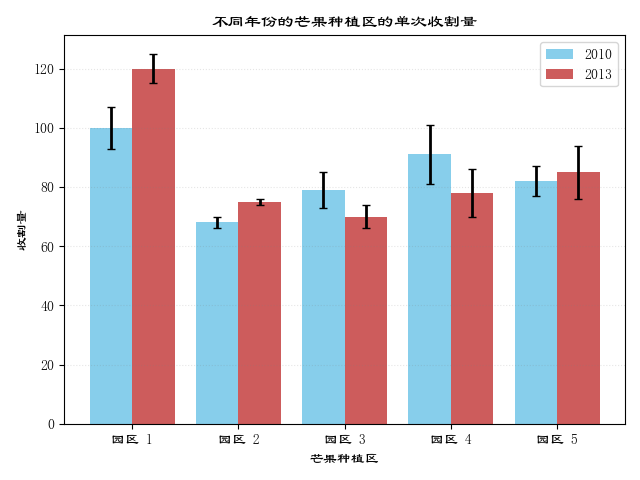
在上面讲述了带误差棒的柱状图的绘制方法,其中的应用场景是有关于“不同芒果种植区的单次收割量”的案例。如果我们尝试进一步比较不同年份的不同芒果种植区的单次收割量的情况,那么就可以借助带误差棒的多数据并列柱状图进行可视化展示。
代码实现
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
mpl.rcParams["font.sans-serif"]=["LiSu"]
mpl.rcParams["axes.unicode_minus"]=False
# some simple data
x = np.arange(5)
y1 = [100,68,79,91,82]
y2 = [120,75,70,78,85]
std_err1 = [7,2,6,10,5]
std_err2 = [5,1,4,8,9]
error_attri = dict(elinewidth=2,ecolor="black",capsize=3)
bar_width = 0.4
tick_label=["园区 1","园区 2","园区 3","园区 4","园区 5"]
# create bar with errorbar
plt.bar(x,y1,
bar_width,
color="#87CEEB",
align="center",
yerr=std_err1,
error_kw=error_attri,
label="2010")
plt.bar(x+bar_width,y2,
bar_width,
color="#CD5C5C",
align="center",
yerr=std_err2,
error_kw=error_attri,
label="2013")
# set x,y_axis label
plt.xlabel("芒果种植区")
plt.ylabel("收割量")
# set xaxis tick_label
plt.xticks(x+bar_width/2,tick_label)
# set title of axes
plt.title("不同年份的芒果种植区的单次收割量")
# set yaxis grid
plt.grid(True,axis="y",ls=":",color="gray",alpha=0.2)
plt.legend()
plt.show()运行结果如图
带误差棒的堆积柱状图
如果我们尝试比较不同地区的图书展览会的图书采购情况,那么我们既可以使用带误差棒的多数据并列柱状图,也可以使用带误差棒的堆积柱状图来呈现图书展销会上订购情况的变化和差异。现在,我们介绍带误差棒的堆积柱状图的绘制方法。
代码实现
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
mpl.rcParams["font.sans-serif"]=["LiSu"]
mpl.rcParams["axes.unicode_minus"]=False
# some simple data
x = np.arange(5)
y1 = [1200,2400,1800,2200,1600]
y2 = [1050,2100,1300,1600,1340]
std_err1 = [150,100,180,130,80]
std_err2 = [120,110,170,150,120]
bar_width = 0.6
tick_label=["家庭","小说","心理","科技","儿童"]
error_attri = dict(ecolor="black",elinewidth=2,capsize=0)
# create bar
plt.bar(x,y1,
bar_width,
color="#6495ED",
align="center",
yerr=std_err1,
label="地区 1",
error_kw=error_attri)
plt.bar(x,y2,
bar_width,
bottom=y1,
color="#FFA500",
align="center",
yerr=std_err2,
label="地区 2",
error_kw=error_attri)
# set x,y_axis label
plt.xlabel("图书种类")
plt.ylabel("订购数量")
# set title
plt.title("不同地区大型图书展销会的图书采购情况")
# set yaxis grid
plt.grid(True,axis="y",ls=":",color="gray",alpha=0.2)
plt.xticks(x,tick_label)
plt.legend()
plt.show()运行结果如图
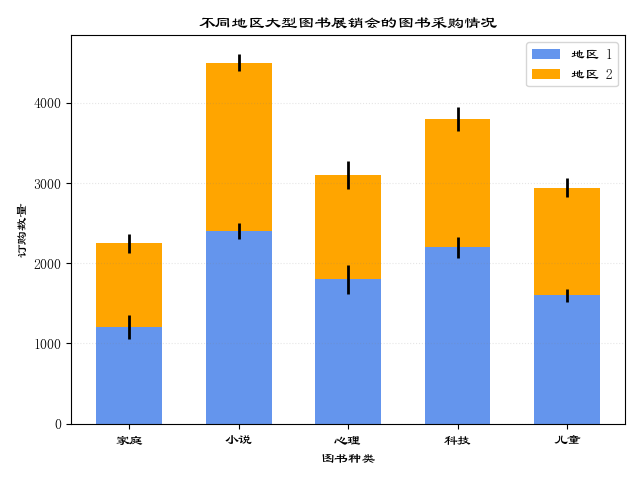
前面我们已经讲解过堆积柱状图的绘制原理了,现在只需要将误差棒添加到堆积柱状图中就可以实现两种统计图形的融合,绘制出带误差棒的堆积柱状图。完成带误差棒的堆积柱状图的绘制任务的关键在于关键字参数 yerr 的使用。因此,只需要向函数 bar()传递关键字参数 yerr 就可以在堆积柱状图的基础上,实现带误差棒的堆积柱状图的绘制任务。
参考资料:《Python 数据可视化之 matplotlib 实践》第三章