图的搜索(图的遍历)是指从图的任一顶点出发,访问图的所有顶点,且每个顶点只访问一次。
深度优先搜索
DFS概念:
深度优先搜索 (Depth-First Search,DFS)是从某个顶点v1出发对图进行搜素,每一步都沿着某一个分支路径向下搜索,当不能继续向下搜索时,则回退到所经过路径的上一个顶点,在回退的过程中所经过的每一个顶点,都尝试寻找未经过的分支向下继续搜索,直到可访问的顶点都被访问。深度优先搜索类似于树的先根遍历。
为了避免顶点被重复访问,需要对已访问的顶点做标记。为了方便描述,将未访问的顶点涂为白色,已访问的顶点涂为黑色。
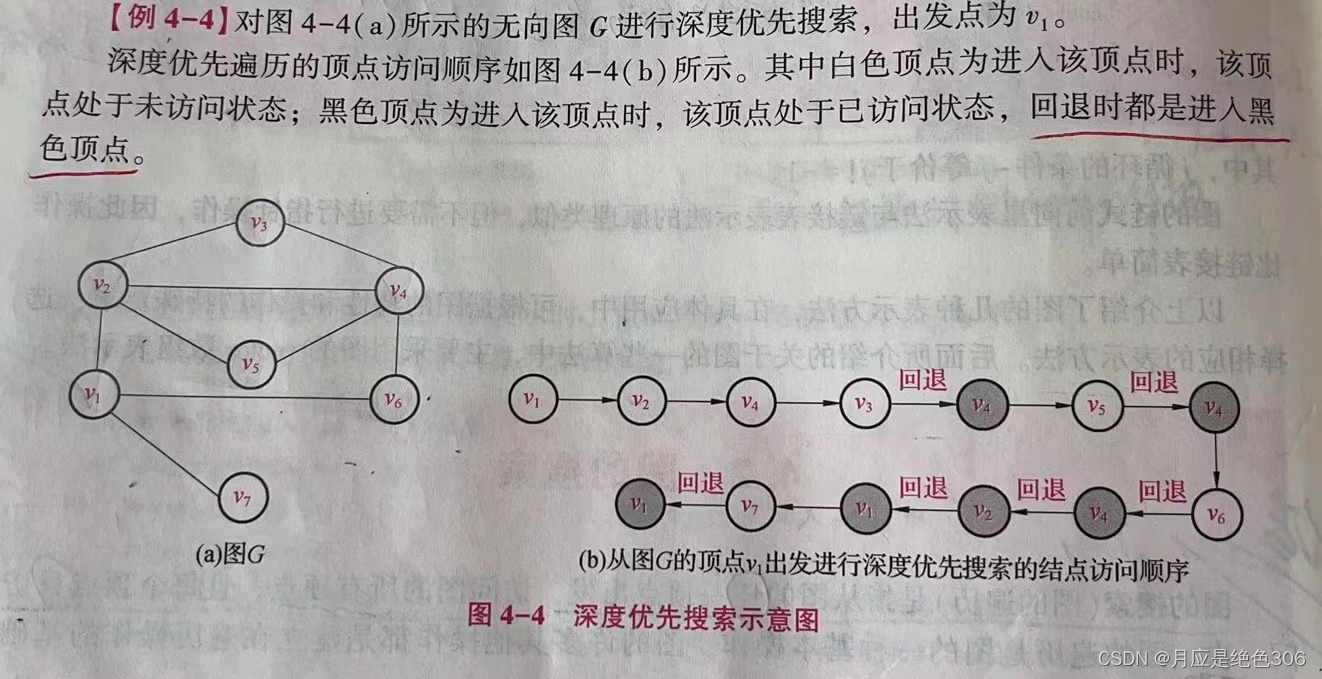
 在搜索过程中,将顶点按照访问的顺序进行编号,称为DFS序列。
在搜索过程中,将顶点按照访问的顺序进行编号,称为DFS序列。
上例中的DFS序列为v1,v2,v4,v3,v5,v6,v7。由于一个顶点出发可能有多重选择,因此DFS序列不唯一。
DFS算法中的回退过程与函数递归或栈的特点比较类似,因此可以采用递归或栈实现DFS。
基于vector数组表示的DFS:
#include<iostream>
#include<vector>
using namespace std;
constexpr auto eNum = 102; //图的顶点数量
constexpr auto vNum = 200; //图的边的数量
typedef string dataType; //图顶点中存放数据信息的类型
typedef int datatype;
constexpr auto INF = 0x3f3f3f3f;
//图的深度优先搜索,以下模板基于vector数组所表示的图(有向图/无向图)
bool vis[vNum]; //标记每一个顶点的颜色
int dfn[vNum], cnt = 0; //dfn存放DFS序列,cnt为序列的编号
//对图g的顶点cur所在的连通分量进行深度优先搜索,初始出发顶点为cur
void dfs(vector<datatype>g[vNum], int cur) {
int i, u;
dfn[++cnt] = cur; //将当前顶点cur的深度优先编号为cnt
vis[cur] = true; //将当前顶点涂为黑色
for (i = 0; i < g[cur].size(); i++) { //检查cur的每一个邻接点
u = g[cur][i];
if (!vis[u]) //u为白色,(cur,u)为树边
dfs(g, u); //从u出发继续搜索
}
}
//对图g进行深度优先搜索,v为顶点的数量
void dfs_traverse(vector<int>g[vNum], int v) {
int i;
memset(vis, 0, sizeof(vis)); //将每个顶点都设置为白色
for (i = 1; i <= v; i++)
if (!vis[i]) //如果存在白色顶点,则从该顶点出发进行深度优先搜索
dfs(g, i);
}
int main() {
}DFS树:
对无向图进行深度优先搜索,如果只保留在 DFS 搜索过程中每一个顶点与白色邻接点之间的边,则可以构成一棵树(森林),称为 DFS 树(森林)。初始出发顶点为 DFS树的根结点,当搜索到顶点u,并从顶点u出发到达其邻接点v时,若v为白色,则将边(u,v)加入DFS树中,且u为v的父结点,则称边(u,v)为图 G的树边;若顶点v为黑色,此时v一定为u的一个祖先结点,则DFS 树中不包含边(u,v),称边(u,v)为图G的回边。如果图G存在回边,则该无向图存在环路。此外,一个结点的子树之间是不存在回边的(若存在,两棵子树便可以合并)。
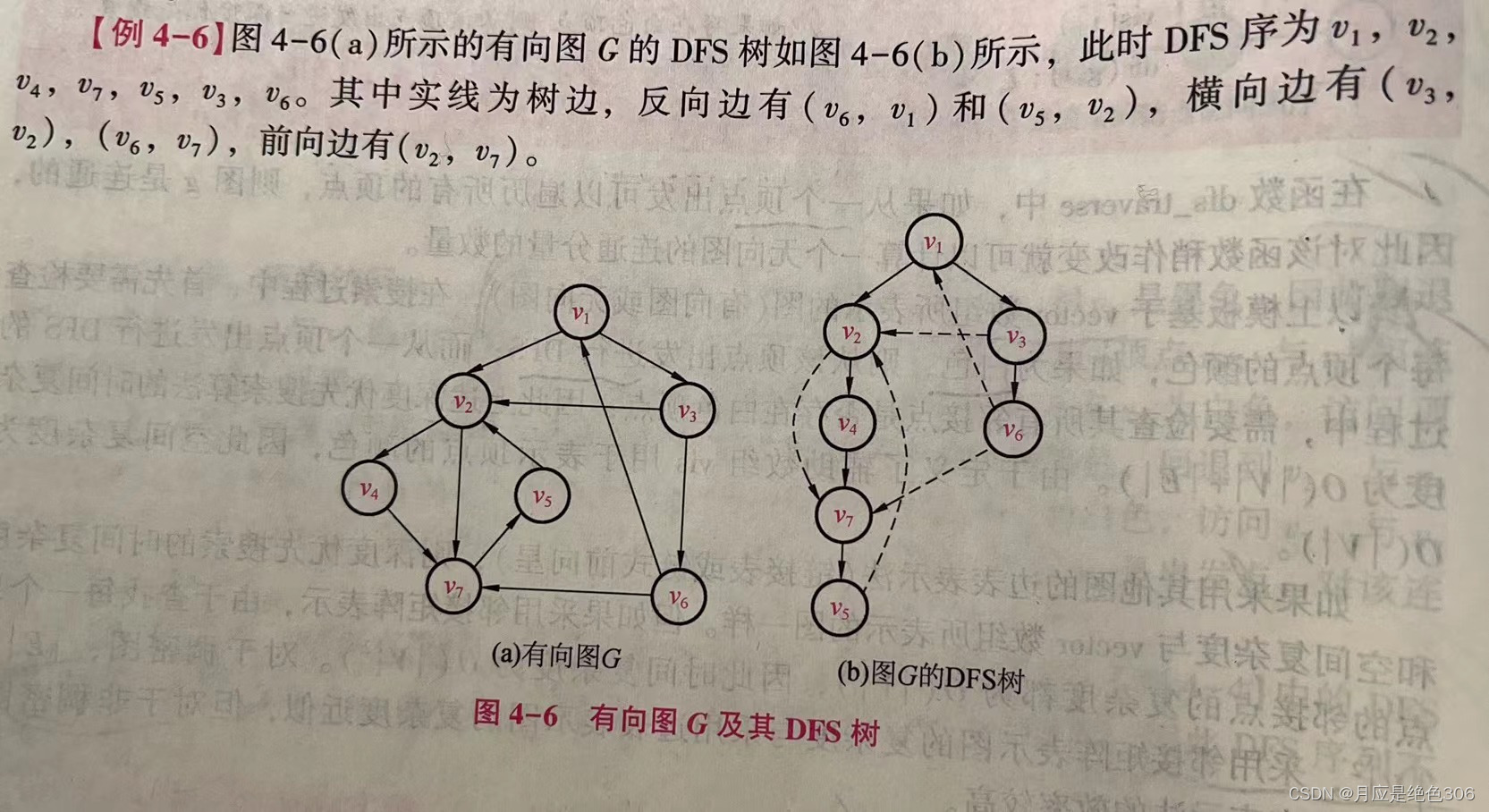
在对有向图进行深度优先搜索所产生的的DFS树中,树边的定义与无向图一样。当从顶点u搜索到顶点v时,如果v为黑色,则分为三种类型:如果v为u的祖先节点,则称(u,v)为反向边;如果v为u的子孙结点,则称(u,v)为前向边;其他情况则称(u,v)为横向边。
深度优先搜索的应用实例
迷宫问题

#include<iostream>
#include<vector>
using namespace std;
constexpr auto N = 100;
constexpr auto M = 100;
typedef int datatype;
constexpr auto INF = 0x3f3f3f3f;
bool maze[N][M], vis[N][M];
int n, m, dir[4][2] = { {1,0},{-1,0},{0,1},{0,-1} };//n和m为迷宫的行数和列数;数组dir为位置的偏移量
//能否到达房间(x,y):(x,y)在迷宫内部;(x,y)能进入;(x,y)为被访问过
bool can(int x, int y) {
return x >= 0 && x < n&& y <= 0 && y < m&& maze[x][y] && !vis[x][y];
}
void dfs(int x, int y,int& ret) {
int i, dx, dy;
vis[x][y] = true;
for (i = 0; i < 4; i++) { //检查四个相邻的房间
dx += x + dir[1][0], dy += y + dir[i][1]; //(dx,dy)为(x,y)的相邻房间
if (dx == n - 1 && dy == m - 1) { //达到右下角
ret = 1;
return;
}
if (can(dx, dy)) { //当(dx,dy)能够到达时,从(dx,dy)出发进行dfs
dfs(dx, dy, ret);
}
}
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
cin >> maze[i][j];
vis[0][0] = true;
int ret = 0;
dfs(0, 0, ret);
cout << ret << endl;
return 0;
}求树的直径:

#include<iostream>
#include<vector>
using namespace std;
constexpr auto eNum = 102; //图的顶点数量
constexpr auto vNum = 200; //图的边的数量
typedef string dataType; //图顶点中存放数据信息的类型
typedef int datatype;
constexpr auto INF = 0x3f3f3f3f;
int dis[vNum];
int vis[vNum];
/*
这里全局数组dis的作用是从顶点u出发进行dfs时,
记录u到其他顶点的路径长度,
当从顶点cur进入顶点v时,dis[v]=dis[cur]+1,
在进行第二次dfs时,需要将dis的每一个值都初始化为0。
*/
//创建vector数组表示的图
void create_vecGraph(vector<int>g[vNum], int v) {
int i=0, e;
while (i<v) {
cin >> e; //输入边数
for (int j = 0; j < e; j++) {
cin >> g[i][j];
}
i++;
}
}
//对图g从顶点cur出发深搜,d为初始点到已搜索到顶点的最长距离,p为最长路径的终点
//时刻进行递归与回溯
void dfs(vector<int>g[vNum], int cur, int& d, int& p) {
int i, v;
vis[cur] = true;
for (i = 0; i < g[cur].size(); i++) {
v = g[cur][i];
if (!vis[v]) {
dis[v] = dis[cur] + 1; //从cur到达v,则初始点到v的距离比到cur的距离多1
if (dis[v] > d) //更新d和p
d = vis[v], p = v;
dfs(g, v, d, p);
}
}
}
int main() {
vector<int>g[vNum];
int v, d = 0, p = 1;
cin >> v;
create_vecGraph(g, v);//创建图(无向无权连通图)
dfs(g, 1, d, p);//从顶点1出发,进行第一次dfs,得到的最长路径的终点为p
memset(dis, 0, sizeof(dis));
memset(vis, 0, sizeof(vis));
d = 0;
dfs(g, p, d, p); //从p出发,进行第二次dfs,得到直径的长度d
cout << d << endl;
}广度优先搜索:
BFS概念
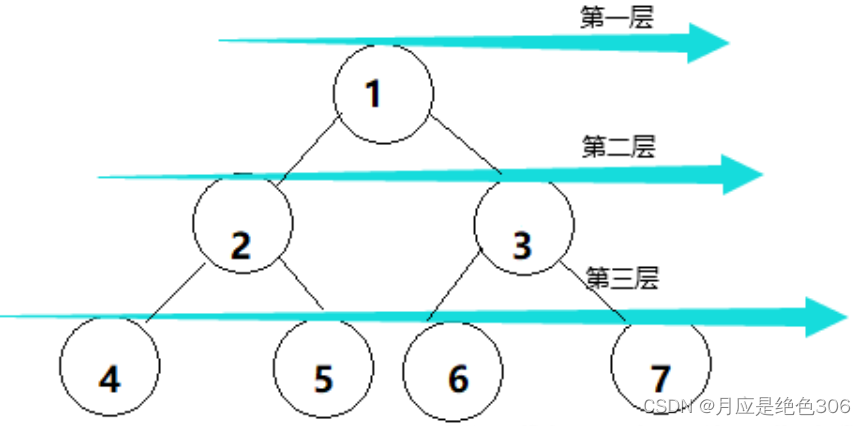
广度优先搜索(BFS)是从某个顶点开始,按层进行遍历,只有当一层所有顶点都遍历后再进入下一层的遍历。广度优先搜索类似于树的按层次遍历。
BFS的实现要借助于队列,即当一个顶点访问结束后,将其所有未被访问且不在队列中的邻接点加入队,排队等待处理。与DFS一样,为了避免顶点被重复访问,将未进入队列的顶点设置为白色,将已进人队列的顶点设置为黑色。为了实现按层操作,在访问一个顶点后,将其所有的白色邻接点加入一个队列,每一次操作都从队头取出一个顶点。
在广度优先搜索过程中,将顶点按照访问的顺序进行编号,称为BFS序列。与DFS序列一样,BFS序列也不唯一。并且,与DFS类似,也用一个数组vis来标记一个顶点的颜色。下列的实现方法使用STL中的queue。
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
constexpr auto eNum = 102; //图的顶点数量
constexpr auto vNum = 200; //图的边的数量
typedef string dataType; //图顶点中存放数据信息的类型
typedef int datatype;
constexpr auto INF = 0x3f3f3f3f;
bool vis[vNum]; //标记顶点的颜色
int bfn[vNum]; //广度优先序列
//对图g中cur所在的连通分量进行广度优先搜索,初始出发点为cur
void bfs(vector<int>g[vNum], int cur) {
int i, u, v, cnt = 0;
queue<int>q;
bfn[++cnt] = cur, vis[cur] = true;
q.push(cur); //将初始出发点加入队列
while (!q.empty()) { //对队列中的元素进行处理,直到队空
u = q.front(), q.pop(); //取出队头元素
for (i = 0; i < g[u].size(); i++) { //检查顶点u的每一个邻接点
v = g[u][i];
if (!vis[v]) { //顶点v为白色
//(u,v)为树边
bfn[++cnt] = v;
vis[v] = true; //加入队列前将v设置为黑色
q.push(v); //将v加入队列
}
}
}
}
//对图g进行广度优先搜索,v为顶点的数量
void bfs_traverse(vector<datatype>g[vNum], int v) {
memset(vis, 0, sizeof(vis));//将每个顶点设置为白色
for (int i = 1; i <= v; i++)
if (!vis[i]) //如果顶点i为白色,则从i出发对其所在的连通分量进行bfs
bfs(g, i);
}
int main() {
}对函数bfs_traverse稍作改变,也可以计算无向图g的连通分量的数量。
与DFS一样,当一轮遍历结束后,BFS也需要检查每一个顶点是否为白色,如果是白色,则从该顶点出发进行遍历,在搜索过程中,需要检查每一条边。
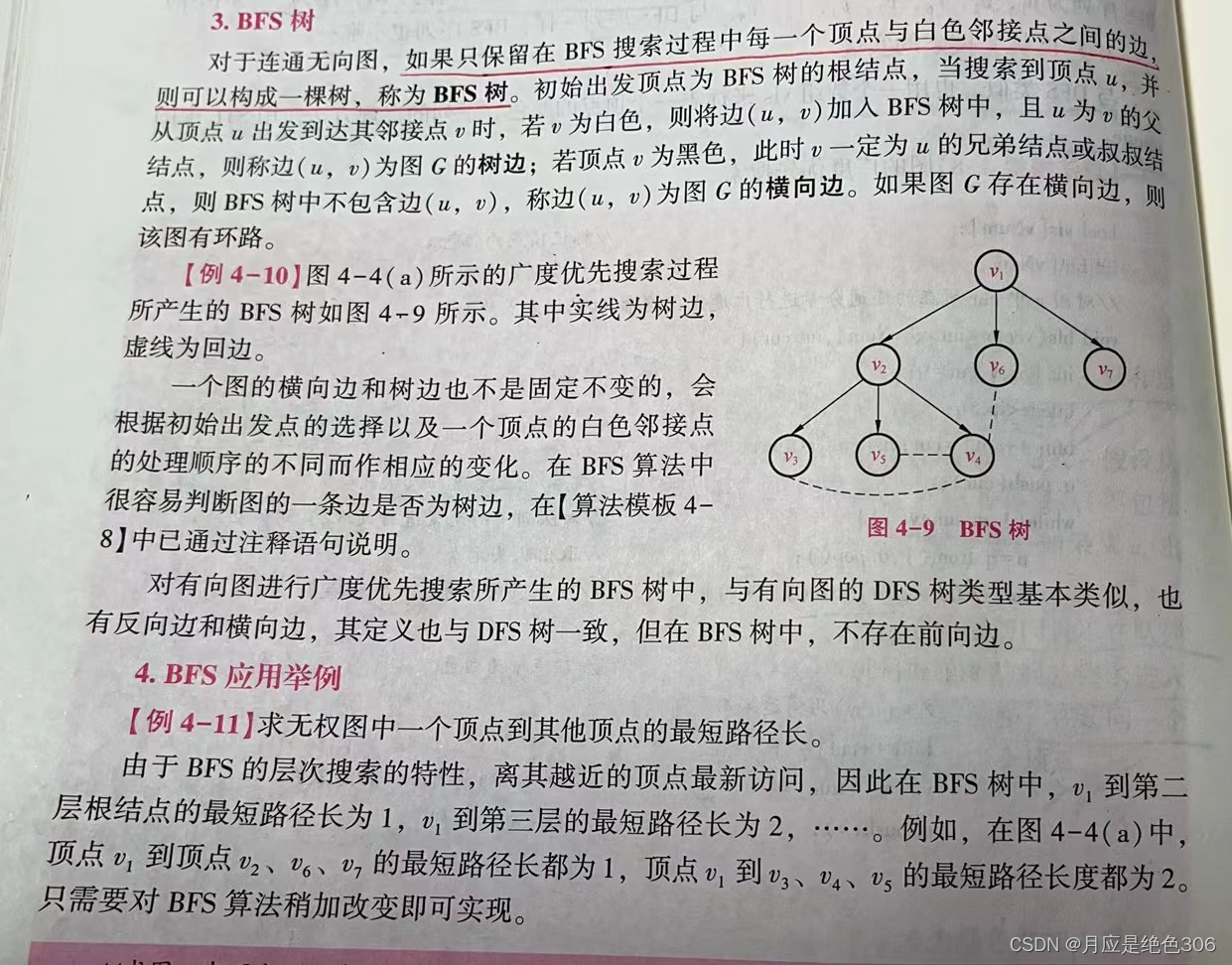
BFS树
//求图g中顶点cur到其他顶点的最短路径长,
//结果保存在数组dis中,假设cur到其他顶点都存在路径
void bfs(vector<int>g[vNum], int cur, int dis[vNum]) {
int i, u, v, cnt = 0;
queue<int>q;
vis[cur] = true;
q.push(cur);
while (!q.empty()) {
u = q.front(), q.pop();
for (i = 0; i < g[u].size(); i++) {
v = g[u][i];
if (!vis[v]) {
dis[v] = dis[u] + 1; //得到cur到v的最短路径长
vis[v] = true, q.push(v);
}
}
}
}