数据挖掘,计算机网络、操作系统刷题笔记38
2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开
测开的话,你就得学数据库,sql,oracle,尤其sql要学,当然,像很多金融企业、安全机构啥的,他们必须要用oracle数据库
这oracle比sql安全,强大多了,所以你需要学习,最重要的,你要是考网络警察公务员,这玩意你不会就别去报名了,耽误时间!
考网警特招必然要考操作系统,计算机网络,由于备考时间不长,你可能需要速成,我就想办法自学速成了,课程太长没法玩
刷题系列文章
【1】Oracle数据库:刷题错题本,数据库的各种概念
【2】操作系统,计算机网络,数据库刷题笔记2
【3】数据库、计算机网络,操作系统刷题笔记3
【4】数据库、计算机网络,操作系统刷题笔记4
【5】数据库、计算机网络,操作系统刷题笔记5
【6】数据库、计算机网络,操作系统刷题笔记6
【7】数据库、计算机网络,操作系统刷题笔记7
【8】数据库、计算机网络,操作系统刷题笔记8
【9】操作系统,计算机网络,数据库刷题笔记9
【10】操作系统,计算机网络,数据库刷题笔记10
【11】操作系统,计算机网络,数据库刷题笔记11
【12】操作系统,计算机网络,数据库刷题笔记12
【13】操作系统,计算机网络,数据库刷题笔记13
【14】操作系统,计算机网络,数据库刷题笔记14
【15】计算机网络、操作系统刷题笔记15
【16】数据库,计算机网络、操作系统刷题笔记16
【17】数据库,计算机网络、操作系统刷题笔记17
【18】数据库,计算机网络、操作系统刷题笔记18
【19】数据库,计算机网络、操作系统刷题笔记19
【20】数据库,计算机网络、操作系统刷题笔记20
【21】数据库,计算机网络、操作系统刷题笔记21
【22】数据库,计算机网络、操作系统刷题笔记22
【23】数据库,计算机网络、操作系统刷题笔记23
【24】数据库,计算机网络、操作系统刷题笔记24
【25】数据库,计算机网络、操作系统刷题笔记25
【26】数据库,计算机网络、操作系统刷题笔记26
【27】数据库,计算机网络、操作系统刷题笔记27
【28】数据库,计算机网络、操作系统刷题笔记28
【29】数据库,计算机网络、操作系统刷题笔记29
【30】数据库,计算机网络、操作系统刷题笔记30
【31】数据库,计算机网络、操作系统刷题笔记31
【32】数据库,计算机网络、操作系统刷题笔记32
【33】数据库,计算机网络、操作系统刷题笔记33
【34】数据库,计算机网络、操作系统刷题笔记34
【35】数据挖掘,计算机网络、操作系统刷题笔记35
【36】数据挖掘,计算机网络、操作系统刷题笔记36
【37】数据挖掘,计算机网络、操作系统刷题笔记37
文章目录
- 数据挖掘,计算机网络、操作系统刷题笔记38
- @[TOC](文章目录)
- 数据挖掘:探索性数据分析(多因子与复合分析)
- 假设检验
- 卡方检验
- 方差检验:f检验
- 相关系数:皮尔森--斯皮尔曼
- 皮尔逊相关系数
- 斯皮尔曼相关系数
- 线性回归:regression
- 主成分分析PCA
- 奇异值分解SVD,也是类似降维的功效
- 然后咱们用代码玩一下,看看这些检验函数都是啥
- t检验
- 看看方差检验的例子
- 做qq图:检验一个分布的分位数,对应正态分布分位数
- 接下里用pandas实现相关系数
- 逻辑回归案例
- PCA变换
- 集线器不管有多少个端口,所有端口都共享一条带宽
- 以太网交换机中的 端口/MAC 地址映射表()
- 关于 TCP 协议的描述中,错误的是 ()
- 临界区是访问共享资源的那段代码,不是用来实现互斥访问的那段代码。
- 计算机系统中判别是否有中断处理事件发生应是在( )?
- 总结
文章目录
- 数据挖掘,计算机网络、操作系统刷题笔记38
- @[TOC](文章目录)
- 数据挖掘:探索性数据分析(多因子与复合分析)
- 假设检验
- 卡方检验
- 方差检验:f检验
- 相关系数:皮尔森--斯皮尔曼
- 皮尔逊相关系数
- 斯皮尔曼相关系数
- 线性回归:regression
- 主成分分析PCA
- 奇异值分解SVD,也是类似降维的功效
- 然后咱们用代码玩一下,看看这些检验函数都是啥
- t检验
- 看看方差检验的例子
- 做qq图:检验一个分布的分位数,对应正态分布分位数
- 接下里用pandas实现相关系数
- 逻辑回归案例
- PCA变换
- 集线器不管有多少个端口,所有端口都共享一条带宽
- 以太网交换机中的 端口/MAC 地址映射表()
- 关于 TCP 协议的描述中,错误的是 ()
- 临界区是访问共享资源的那段代码,不是用来实现互斥访问的那段代码。
- 计算机系统中判别是否有中断处理事件发生应是在( )?
- 总结
数据挖掘:探索性数据分析(多因子与复合分析)

多因子:
探索属性与属性之间的关联关系

假设检验
根据已知分布,推断假设成立的概率
原假设H0
备择假设H1,非H0
选择检验统计量
根据alpha(0,05),确定拒绝域
95%可能性符合分布A
则显著性水平就是5%,拒绝
计算p值或者样本统计值,做出判断
通过例子说明问题
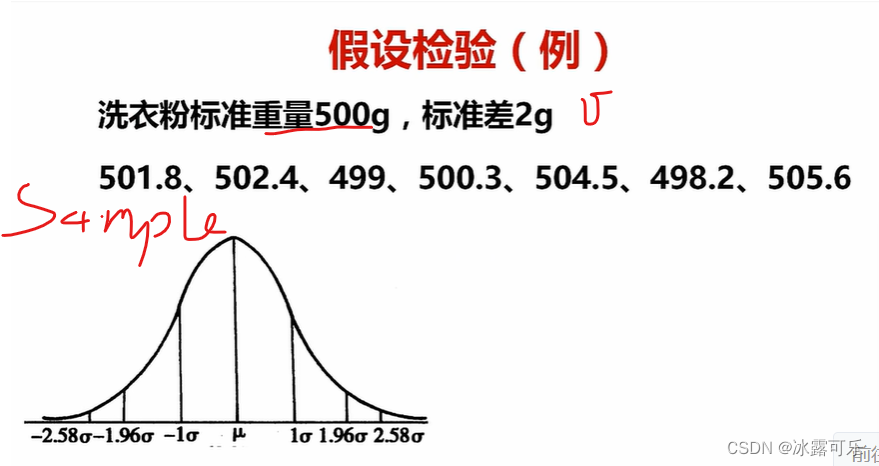
看看它符合要求吗???
H0原假设:样本符合均值500g的,sigma为2的正态分布
H1备择假设,样本不符合:均值500g的,sigma为2的正态分布
构造统计量
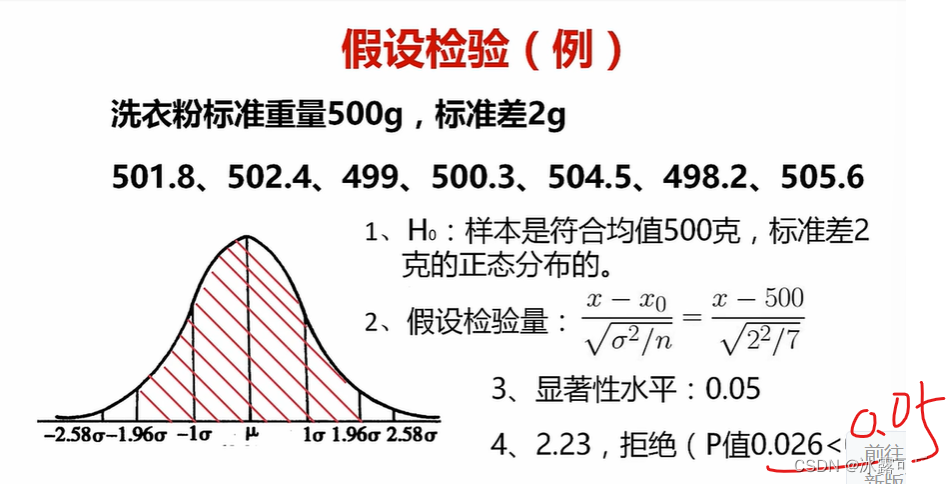
p就是上面那个检验量2.23倍sigma到无穷大的累计概率:0.013【单边】
如果是双边检验p概率
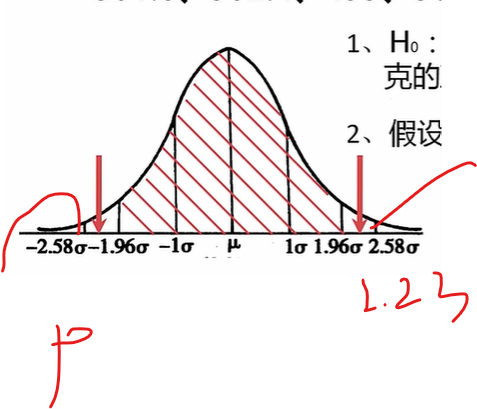
那2.23怎们来的,上面统计量的均值吧
总之,它求出来是sigma的2.23倍,得到的概率是落入了拒绝域了
gg
因此,这个样本不咋地,H0是错误的
H1是正确的
卡方检验
当统计量不同,导致检验的方法命名就不同了
看看化妆和性别有关吗??
卡方检验的目的就是看看俩参数之间是否有联系呢????

原假设H0,化妆与性别无关
备择假设H1:化妆和性别有关
也就是说,男女化妆的数量应该是平均的np个
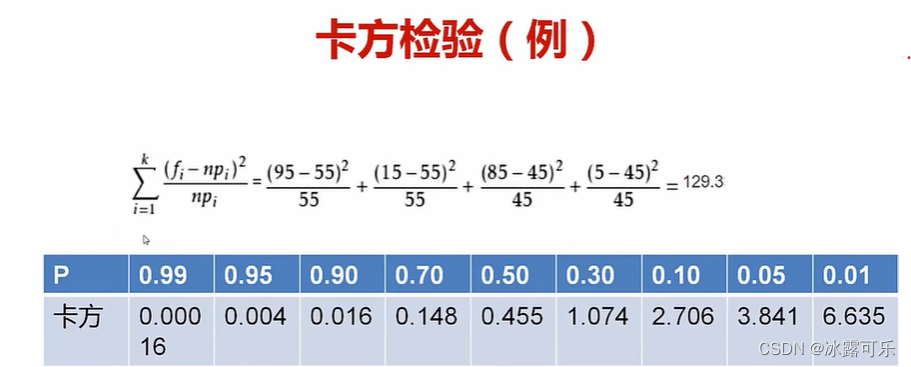
但是呢卡方值,算一波所有数据相对于均值的平方差
再加权平均
看看卡方值是多少
再利用卡方值与p对应的大小
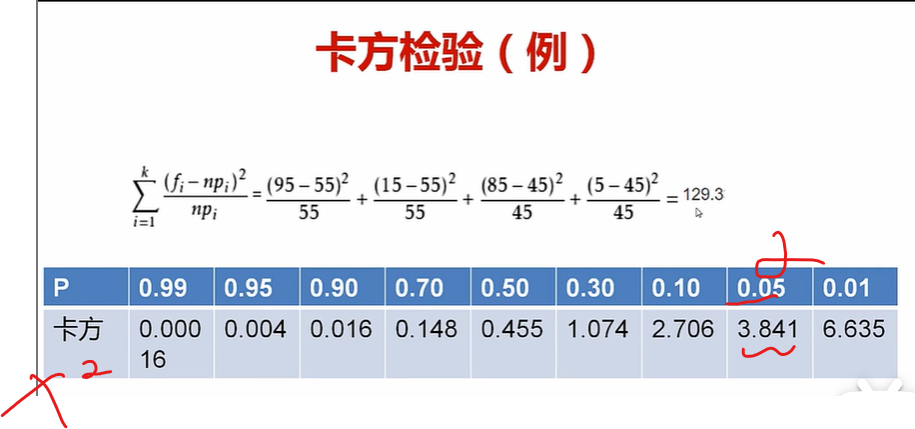
如果说alpha是005
那要求卡方值为3.841
但是这里129远大于3.841,导致p值<alpha
落入了拒绝域
显然H0不成立啊
gg
这就是这个统计量卡方带来的好处
骚不骚
很明显化妆和性别关系很大的
方差检验:f检验
方差检验的目的是啥呢???
多个样本,检验不同参数两两之间的是否有关呢??
就同时检验多个参数之间的关系
比如,看看三种电池,他们三者寿命的均值之间是否有差别
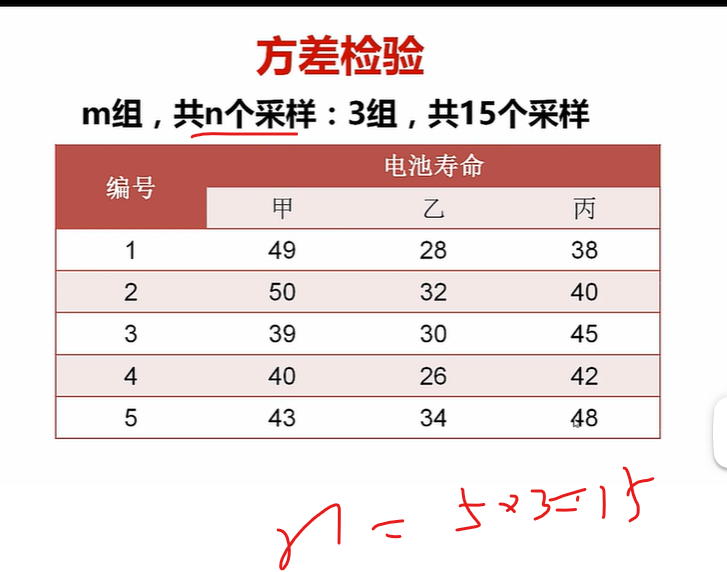
介绍仨公式
ni是每一组的样本大小,这里就是5
xhat是总体样本的均值【甲乙丙仨整体的均值】
xihat是每一个小组i的均值【比如甲电池的均值】

SS之平方和
SST:总变差平方和
SSM:组间平方和
SSE:组内残差平方和

统计量是这个F
原假设H0,均值无差别
H1,有差别

F对应的p表查询出来,发现,它又落入了拒绝域
因此呢,这H0又gg
显然就是三种电池寿命的均值还是有差异的
相关系数:皮尔森–斯皮尔曼
评价两组数据的相关关系
【-1,0,1】
正相关,无关,负相关
皮尔逊相关系数

斯皮尔曼相关系数
计算公式不同
排名名次差d
从小到大的排名哦

与具体的数值没有关系
只看排名哦
这个玩意更美
线性回归:regression
拟合一个函数f
确定2个以上的变量的依赖关系
看看y和x是啥关系
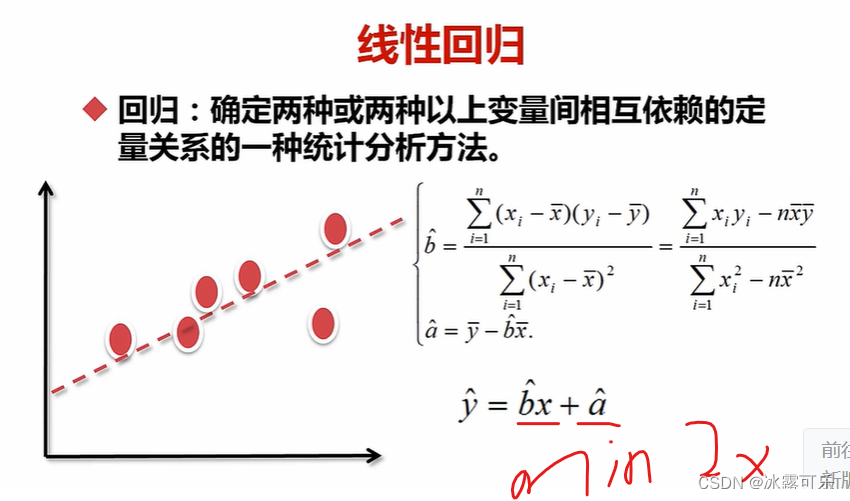
最小二乘法
先确定bhat
然后用y的均值-bhant*x均值
就确定了参数
好说
如何评价你这个方法呢?
决定系数和残差不相关

多个参数k个就是右边的公式
残差DW检验
e是残差
预测值-实际测
得到的残差排序
套入公式:
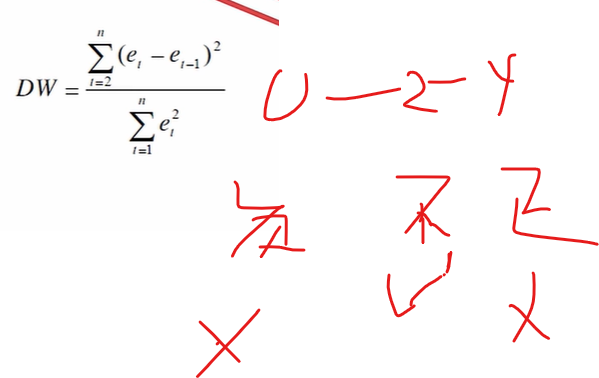
DW是2的话,代表不相关
说明你这个回归很好
DW是0或者4都不好
主成分分析PCA
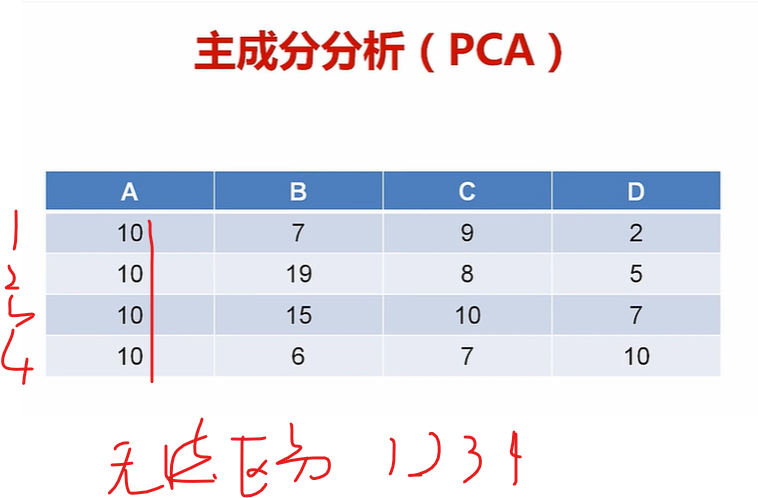
比如大家都是1.7,你怎么知道它是男女????
根据某些属性特征,可以更好区分数据
把不重要的干掉
留下的特征就是主成分
分为几个步骤:

给你一个表,
里面有俩字段xy
数据有很多条,看看你能
否掏出主成分来,到底x决定了每行分类,还是y?
还是xy都的要
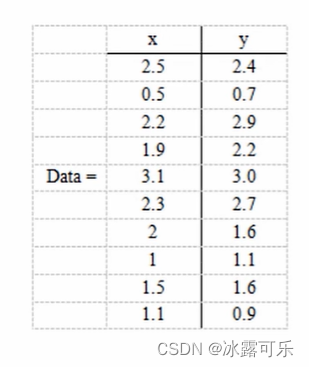
协方差矩阵
求特征值和特征向量
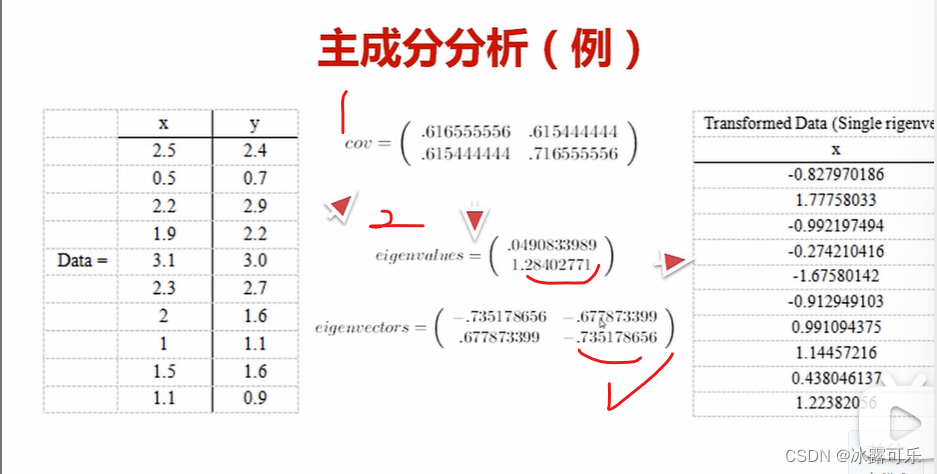
选取大的那个特征值
然后×【x-x均值,y-y均值】
得到新的一个data的主成分矩阵x
拿这个矩阵x就能区分data每行的类别
你说呢?
这就是主成分分析
不用俩xy
将xy两位直接降维了
变为x一个维度
y是没必要的,懂?
尽可能失真小,计算量也小
类似的
奇异值分解SVD,也是类似降维的功效

U是正交基
V是变换后空间的正交基

这个r把规模缩小,
西格玛矩阵r*r
用它替代分析A,其实也是降维的方法
这是研究生学习的矩阵论课程里面的东西
然后咱们用代码玩一下,看看这些检验函数都是啥
生成正态分布的数据,比如20个
用scipy里面的stats函数
import numpy as np
import scipy.stats as ss
# 正态分布所需包
def f1():
# 确定正态分布是否符合呢?
data_norm = ss.norm.rvs(size=20)
print(data_norm)
if __name__ == '__main__':
f1()
[ 0.09411281 -1.97450672 1.64045422 0.06071294 2.12194966 1.52693092
-1.39221609 -1.06628155 0.25081274 -1.40537914 0.01396742 0.16219329
-0.33560058 -1.44778573 0.17050319 2.16088047 -0.35409283 -1.0338166
-0.94215183 -0.4328557 ]
你咋知道这个玩意数据,确实是正态分布呢
咱们检验一把即可
算算normaltest(data)
import numpy as np
import scipy.stats as ss
# 正态分布所需包
def f1():
# 确定正态分布是否符合呢?
data_norm = ss.norm.rvs(size=20)
print(data_norm)
print(ss.normaltest(data_norm)) # 如果pvalue在0.05拒绝域之外,就是合理的接受
if __name__ == '__main__':
f1()
[-0.74882013 -0.58863065 -1.48061786 1.28240066 -0.83784683 -1.58562203
0.51225961 -0.2455727 0.39191626 0.52623345 -0.34591658 -1.87471517
-2.22444904 0.82917589 -0.04721069 3.01761533 0.7300005 -0.08607988
-0.56857694 -0.11541347]
NormaltestResult(statistic=3.6751041403325004, pvalue=0.15920667625655693)
你看看
p
在接受域内的
好说
咱们看看上次那个例子

用一个函数chi2_contingency
来做卡方检验
def f2():
# 你要检验啥,矩阵直接放入函数
matrix = [[15,95],
[85,5]]
# 这个矩阵列: 男 女
# 化妆人数 15 95
# 不化妆人数 85 5
# 你直接将其灌入卡方检验的函数,它自己跑
print(ss.chi2_contingency(matrix))
# 你看看它的检验统计量,p值,自由度,理论好分布
if __name__ == '__main__':
f2()
(126.08080808080808, 2.9521414005078985e-29, 1, array([[55., 55.],
[45., 45.]]))
结果展示
统计量是126,跟上次算的129差不多
p值是超级超级小的一个数:2.9521414005078985e-29
直接落入了0.05的拒绝域
gg
显然你的假设不成立,就是说化妆和性别是有关的哦
而且理论分布应该是一半一半的量
但是显然,这分布是不对劲的
懂???
这就是卡方检验,这函数,你需要了解,方便用的时候用
t检验

俩样本是否独立呢?
比如:
def f3():
# 你要检验啥,矩阵直接放入函数
a = [15,95]
b = [85,5]
# 这个矩阵列: 男 女
# 化妆人数 15 95
# 不化妆人数 85 5
# 你直接将其灌入卡方检验的函数,它自己跑
print(ss.ttest_ind(a, b))
# 你看看它的检验统计量,p值,自由度,理论好分布
if __name__ == '__main__':
f3()
Ttest_indResult(statistic=0.17677669529663687, pvalue=0.8759652654107916)
这pvalue是大于0.05的,显然他们独立
比如你随机产生俩正态分布数据,看看这俩数据他们是独立的吗?
a = ss.norm.rvs(size=10)
b = ss.norm.rvs(size=10)
print(ss.ttest_ind(a, b))
Ttest_indResult(statistic=-0.004294053507082778, pvalue=0.9966210845232548)
pvalue远大于0.05直接就是接受域内合理的取值
美滋滋
看看方差检验的例子

def f4():
# 你要检验啥,矩阵直接放入函数
matrix = np.array([[49,28,38],
[50,32,40],
[39,30,45],
[40,26,42],
[43,34,48]])
print(type(matrix))
print(matrix[:, 0])
# 这个矩阵列: 甲乙丙
# 多行数据
# 看看仨电池均值间是否相同?三组数据
print(ss.f_oneway(matrix[:, 0], matrix[:, 1], matrix[:, 2]))
if __name__ == '__main__':
f4()
<class 'numpy.ndarray'>
[49 50 39 40 43]
F_onewayResult(statistic=17.619417475728156, pvalue=0.0002687153079821641)
方差检验的结果你看看,pvalue在拒绝域
所以他们的均值并不相同
做qq图:检验一个分布的分位数,对应正态分布分位数
检验一个分布是否为正态分布
如果分位数刚刚好y=x
那就说明这个分布它是正态分布
用啥包呢?
statsmodels包
里面的
from statsmodels.graphics.api import qqplot
import matplotlib.pyplot as plt
def f5():
# 你要检验啥,矩阵直接放入函数
qqplot(ss.norm.rvs(size=100))
plt.show()
# 检验一个分布是否为正态分布
if __name__ == '__main__':
f5()
qq图形包
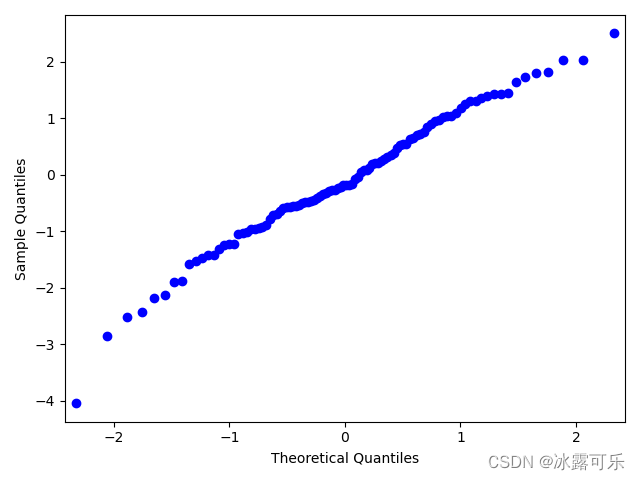
横轴是你正态分布的分位数
纵轴是你的样本分布分位数
他们可以组合成y=x的曲线
美滋滋
所以你的样本确实是正太分布
很牛
接下里用pandas实现相关系数
构造俩序列
看看他们相关与否
import pandas as pd
def f6():
# 你要检验啥,矩阵直接放入函数
# 构造系数
a = pd.Series([1,2,3,4,5,6,7])
b = pd.Series([2,3,4,5,6,7,8])
print(a.corr(b, method='pearson'))
print(a.corr(b, method='spearman'))
if __name__ == '__main__':
f6()
1.0
1.0
很稳的
假如你要看到
import pandas as pd
def f6():
# 你要检验啥,矩阵直接放入函数
# 构造系数
a = pd.Series([1,2,3,4,5,6,7])
b = pd.Series([2,3,4,5,6,7,8])
# print(a.corr(b, method='pearson'))
# print(a.corr(b, method='spearman'))
# 咱们可以对ab拼接起来的dataframe来做相关性计算
# 由于df是对列计算相关性系数,那就需要搞成arr,再转置
df = pd.DataFrame(np.array([a,b]).T)
print(df)
print(df.corr()) # 默认皮尔森
if __name__ == '__main__':
f6()
0 1
0 1 2
1 2 3
2 3 4
3 4 5
4 5 6
5 6 7
6 7 8
0 1
0 1.0 1.0
1 1.0 1.0
看见没,两列数据
逻辑回归案例
sklearn官网学习:
直接搜线性linear
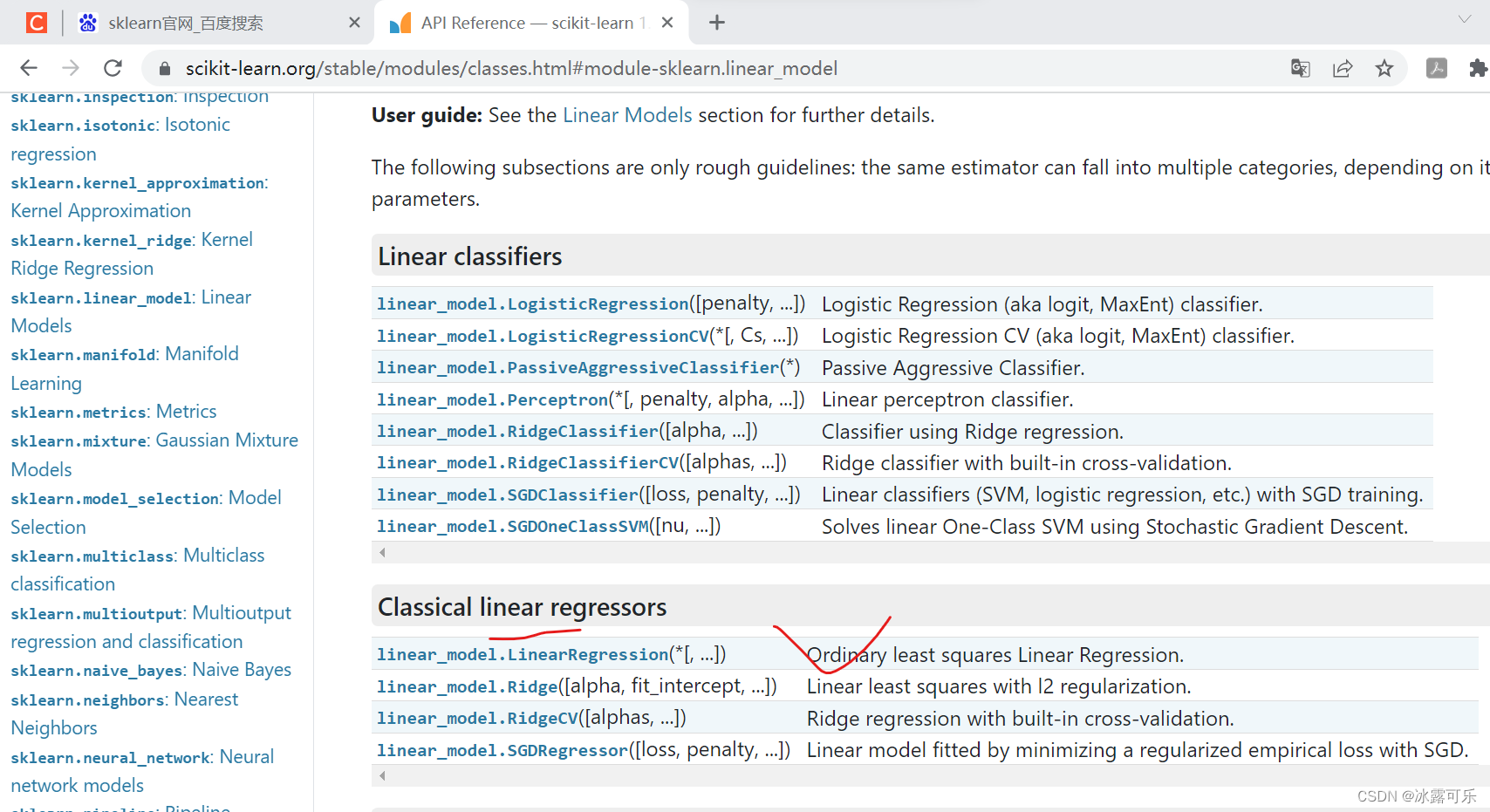
点进去
from sklearn.linear_model import LinearRegression
def f7():
x = np.arange(10).astype(np.float).reshape((10, 1)) # 生成10*1的数据
y = 3*x + 4 + np.random.random((10, 1)) # 0--1的随机数
# print(x)
# print(y)
# 然后我定义一个线性回归模型
reg = LinearRegression()
# fit拟合
ans = reg.fit(x, y) # x轴,y结果,想办法找到ab,拟合y=ax+b
y_pred = reg.predict(x) # 拟合好之后,模型灌入x,输出预测值
print(y_pred)
if __name__ == '__main__':
f7()
[[ 4.88722202]
[ 7.8027851 ]
[10.71834817]
[13.63391124]
[16.54947431]
[19.46503738]
[22.38060046]
[25.29616353]
[28.2117266 ]
[31.12728967]]
再看参数
# 你可以看看参数里面的斜率,和截距
print(reg.coef_, reg.intercept_)
[[3.02968728]] [4.33388888]
其实这个拟合很稳了
就是刚刚我们刚刚说的3和4
PCA变换

data就上面这个
from sklearn.decomposition import PCA
def f8():
# PCA
data = np.array([np.array([2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1]),
np.array([2.4,0.7,2.9,2.2,3,2.7,1.6,1.1,1.6,0.9])]).T
# 是一个两列哦
print(data)
# sklearn就有降维的PCA
lower = PCA(n_components=1) # 希望降维到1
lower.fit(data)
# 然后利用transform函数,直接得到降维之后的数据
print(lower.fit_transform(data))
# 你可以看看这个lower的信息量
print(lower.explained_variance_ratio_)
if __name__ == '__main__':
f8()
[[2.5 2.4]
[0.5 0.7]
[2.2 2.9]
[1.9 2.2]
[3.1 3. ]
[2.3 2.7]
[2. 1.6]
[1. 1.1]
[1.5 1.6]
[1.1 0.9]]
[[-0.82797019]
[ 1.77758033]
[-0.99219749]
[-0.27421042]
[-1.67580142]
[-0.9129491 ]
[ 0.09910944]
[ 1.14457216]
[ 0.43804614]
[ 1.22382056]]
[0.96318131]
你可以看降维之后的数据
也可以看到信息量仍然是96%,很高
集线器不管有多少个端口,所有端口都共享一条带宽
链接:https://www.nowcoder.com/questionTerminal/61db5a3a8bfe436aa5e2cd60da9afc81
来源:牛客网

集线器不管有多少个端口,所有端口都共享一条带宽,在同一时刻只能有两个端口传送数据,其他端口只能等待;只能工作在半双工模式下。交换机每个端口都有一条独占的带宽,当两个端口工作时并不影响其他端口的工作,交换机可以工作在半双工模式下也可以工作在全双工模式下。
以太网交换机中的 端口/MAC 地址映射表()

- 首先,以太网交换机(或第二层交换机)实际上就是一个多接口的网桥。
- 是一种即插即用设备,其内部的帧转发表是通过自学习算法自动地逐渐建立起来的。
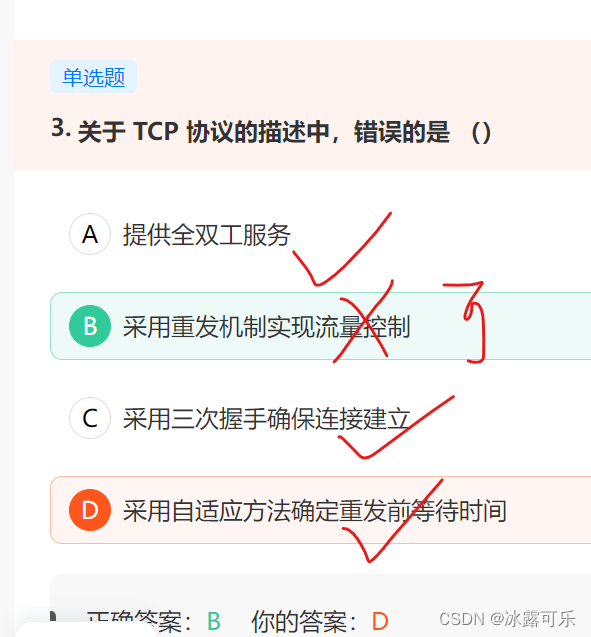
关于 TCP 协议的描述中,错误的是 ()
链接:https://www.nowcoder.com/questionTerminal/0c2485dc9aa64c76b082eee6a751b756
来源:牛客网
TCP提供一种基于滑动窗口协议的流量控制机制。
在通信过程中,接收方根据自己接收缓存的大小,动态地调整发送方的发送窗口大小,这就是接受窗口rwnd,即调整TCP报文段首部中的“窗口”字段值,来限制发送方向网络注入报文的速率。同时,发送方根据其对当前网络拥塞程度的估计而确定的窗口值,称为拥塞窗口cwnd,其大小与网络的带宽和时延密切相关。
TCP使用了校验、序号、确认和重传等机制来实现可靠传输
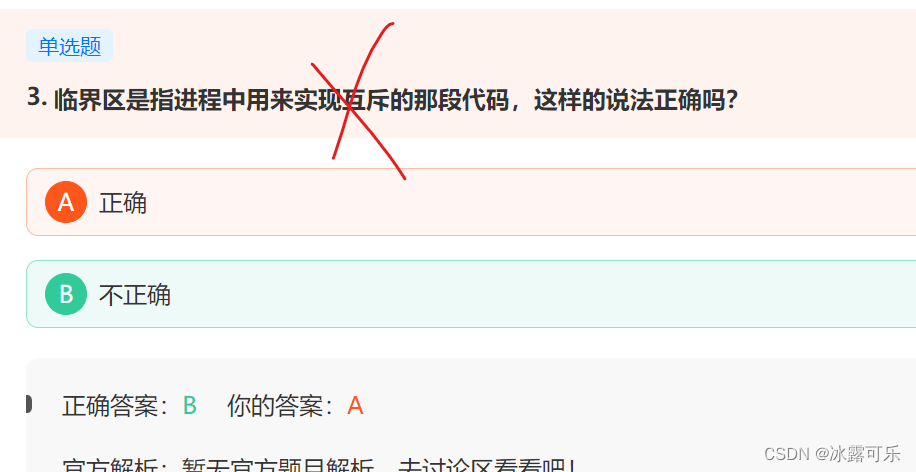
临界区是访问共享资源的那段代码,不是用来实现互斥访问的那段代码。
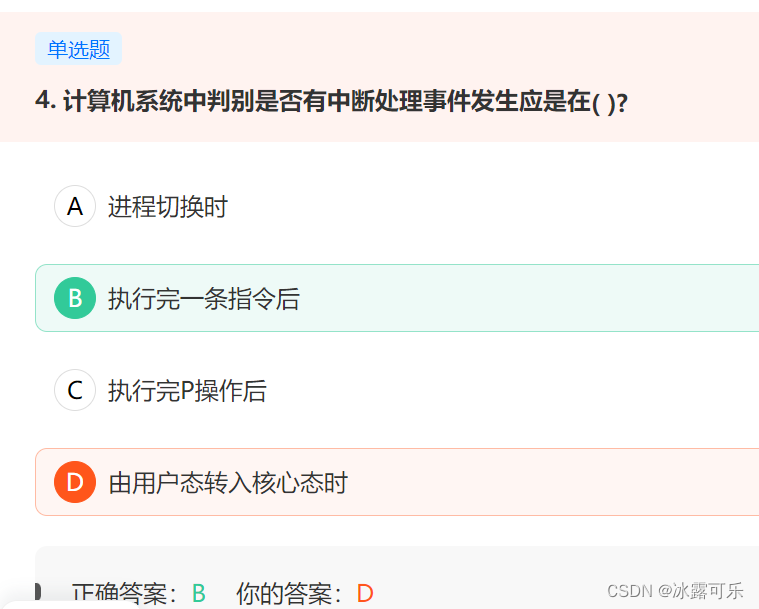
计算机系统中判别是否有中断处理事件发生应是在( )?
总结
提示:重要经验:
1)
2)学好oracle,操作系统,计算机网络,即使经济寒冬,整个测开offer绝对不是问题!同时也是你考公网络警察的必经之路。
3)笔试求AC,可以不考虑空间复杂度,但是面试既要考虑时间复杂度最优,也要考虑空间复杂度最优。