文章目录
- 前言
- 一、认识快速幂
- 二、快速幂思路及代码
- 三、矩阵快速幂
- 3.1、矩阵乘法代码实现
- 3.2、矩阵快速幂代码实现
- 参考资料
前言
在学习Acwing c++蓝桥杯辅导课第九讲复杂DP-AcWing 1303. 斐波那契前 n 项和时有使用到矩阵快速幂算法,这里来记录下知识点正好也将快速幂部分也整合下。
当前文章已收录到博客文件目录索引:博客目录索引(持续更新)
一、认识快速幂
快速幂就是快速算底数的n次幂。其时间复杂度为 O(log₂N), 与朴素的O(N)相比效率有了极大的提高
问题引出:7的10次方,怎样算比较快?
原理
快速幂算法的核心思想就是每一步都把指数分成两半,而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小,所需要执行的循环次数也变小,而最后表示的结果却一直不会变。
//可以看到由原先的n次倍数相乘之后转变来让运行次数大大减小
3^10=3*3*3*3*3*3*3*3*3*3
3^10=(3*3)*(3*3)*(3*3)*(3*3)*(3*3)
3^10=(3*3)^5
3^10=9^5
9^5=(9^4)*(9^1)
9^5=(6561^1)*(9^1)
通过使用快速幂,能够将时间复杂度降低为log2N
二、快速幂思路及代码
核心二分思路:拆分为三种情况,①n为奇数。②n为偶数。③n=0。
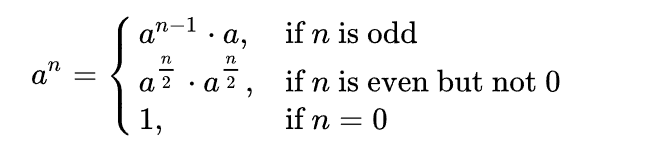
/**
* @ClassName 快速幂
* @Author ChangLu
* @Date 4/18/2022 7:28 PM
* @Description 快速幂求解
*/
public class 快速幂 {
//取模操作(对大素数取模)
private static final long MOD = 1000000007;
public static void main(String[] args) {
// System.out.println(qpow(2, 3));
System.out.println(qpow2(2, 100000000));
}
/**
* 递归快速幂
* @param a 实数a
* @param n 阶数n,三种情况,n=0,n=奇数,n=偶数
* @return
*/
public static long qpow(long a, long n){
if (n == 0){
return 1;
}else if ((n & 1) == 1) { //奇数
return qpow(a, n -1) * a % MOD;
}else {
long temp = qpow(a, n / 2) % MOD;
return temp * temp % MOD;
}
}
/**
* 非递归方式
*/
public static long qpow2(long a, long n) {
long ans = 1;
while ( n != 0) {
if ((n & 1) == 1) { //若是n为奇数
ans *= a % MOD;
ans %= MOD;//求模处理
}
a *= a % MOD; //这个就表示偶数情况
a = a % MOD;//求模处理
n = n >> 1;
}
return ans;
}
}
三、矩阵快速幂
3.1、矩阵乘法代码实现
首先先了解下矩阵乘法:
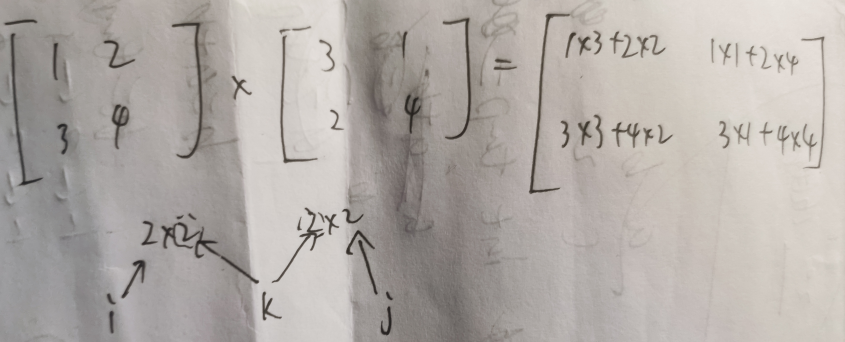
模板:
//i与j来进行用来定位结果矩阵中的下标 k则是用来使用第i列数字*第j列数字
for (int i = 0; i <= 2; i ++ )
for (int j = 0; j <= 2; j ++ )
for (int k = 0; k <= 2; k ++ )
c[i][j] += a[i][k] * b[k][j];
测试代码:
import java.util.Arrays;
public class Main {
static final int[][] a = {
{1, 2},
{3, 4}
};
static final int[][] b = {
{3, 1},
{2, 4}
};
//矩阵乘法
//返回的是a*b矩阵的结果矩阵
public static int[][] multi(int a[][], int b[][]) {
int x = a.length, y = b[0].length, z = b.length;
int[][] ans = new int[x][y];
for (int i = 0; i < x; i++)
for (int j = 0; j < y; j++)
for (int k = 0; k < z; k++)
ans[i][j] += a[i][k] * b[k][j];
return ans;
}
public static void main(String[] args) {
//矩阵乘法
int[][] c = multi(a, b);
for (int[] arrs : c) {
System.out.println(Arrays.toString(arrs));
}
}
}
3.2、矩阵快速幂代码实现
若是矩阵为A,来让我们求An此时若是我们可以实现矩阵快速幂,代码模板如下:
//n表示的乘的次数
while (n != 0) {
//n为奇数情况
if ((n & 1) == 1) ans = mult(ans, A);
//n为偶数情况
mult(A, A);
n >>= 1;
}
实际案例代码:矩阵快速幂
import java.util.Arrays;
public class Main {
static final int[][] a = {
{1, 2},
{3, 4}
};
static final int[][] b = {
{3, 1},
{2, 4}
};
//矩阵乘法
//返回的是a*b矩阵的结果矩阵
public static int[][] multi(int a[][], int b[][]) {
int x = a.length, y = b[0].length, z = b.length;
int[][] ans = new int[x][y];
for (int i = 0; i < x; i++)
for (int j = 0; j < y; j++)
for (int k = 0; k < z; k++)
ans[i][j] += a[i][k] * b[k][j];
return ans;
}
//矩阵快速幂
public static int[][] pow_multi(int a[][], int n) {
int m = a.length;
//初始化ans结果矩阵
int ans[][] = new int[m][m];
for (int i = 0; i < m; i ++) {
for (int j = 0; j < m; j ++) {
if (i == j) ans[i][j] = 1;
}
}
//写法基本与整数快速幂一致
while (n != 0) {
if ((n & 1) == 1) ans = multi(ans, a);
a = multi(a, a);
n >>= 1;
}
return ans;
}
public static void main(String[] args) {
//矩阵乘法
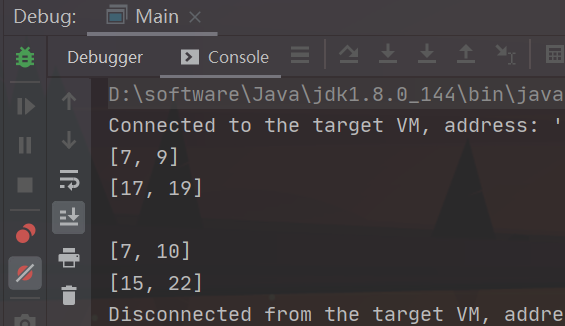
int[][] c = multi(a, b);
for (int[] arrs : c) {
System.out.println(Arrays.toString(arrs));
}
System.out.println();
//快速幂
int[][] d = pow_multi(a, 2);
for (int[] arrs : d) {
System.out.println(Arrays.toString(arrs));
}
}
}
参考资料
[1]. 蓝桥杯软件类备赛:快速幂和矩阵快速幂
[2]. 「算法小知识」如何计算快速幂(上):快速幂。
[3]. 算法学习笔记(4):快速幂:该文章不错可以学习。