1.素数的定义
- 素数又称质数。
- 质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。
- 一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;否则称为合数(规定1既不是质数也不是合数)。
2.问题引入:如何在数据规模较大的情况下高效的求解?

3.朴素解法
// 找出小于n的所有素数的方法
public static List<Integer> findPrimes(int n) {
List<Integer> primes = new ArrayList<>();
for (int num = 2; num < n; num++) {
if (isPrime(num)) {
primes.add(num);
}
}
return primes;
}
// 判断一个数是否为素数的方法
private static boolean isPrime(int num) {
if (num <= 1) {
return false;
}
//注意这里只需要遍li到根号num即可
//
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) {
return false;
}
}
return true;
}

在数据规模较大的情况下,这种暴力解法效率低下,是不可取的。
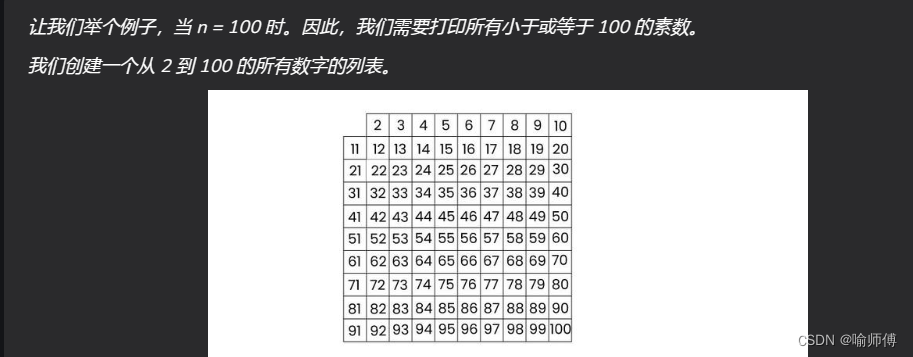
4.Sieve of Eratosthenes(埃拉托斯特尼筛法)
The sieve of Eratosthenes is one of the most efficient ways to find all primes smaller than n when n is smaller than 10 million or so.
埃拉托色尼筛法是找到小于n的所有质数的最有效方法之一当n小于1000万左右时。
When the algorithm terminates, all the numbers in the list that are not marked are prime.
当算法结束时,列表中所有未标记的数字都是素数。
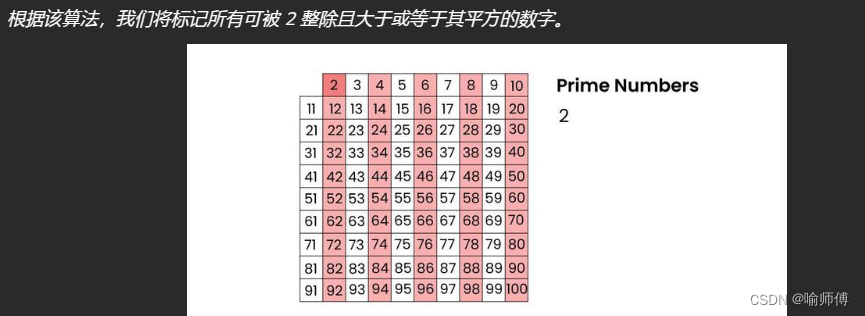
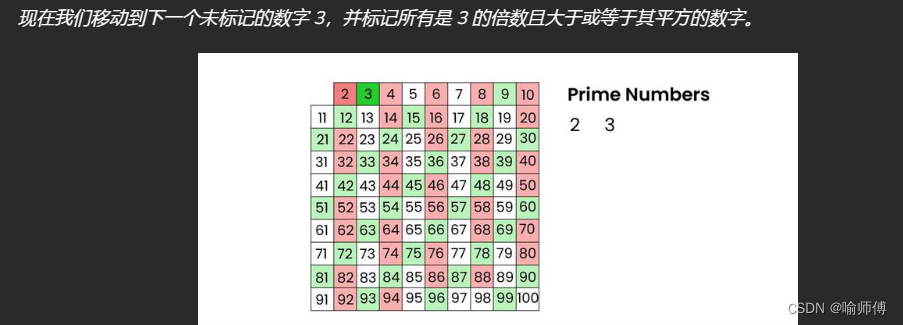
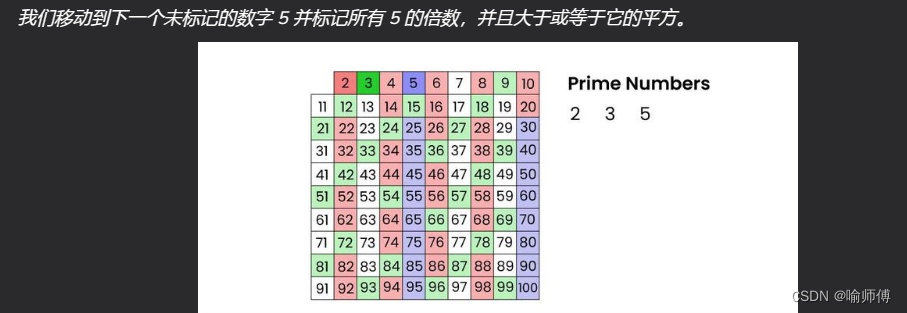
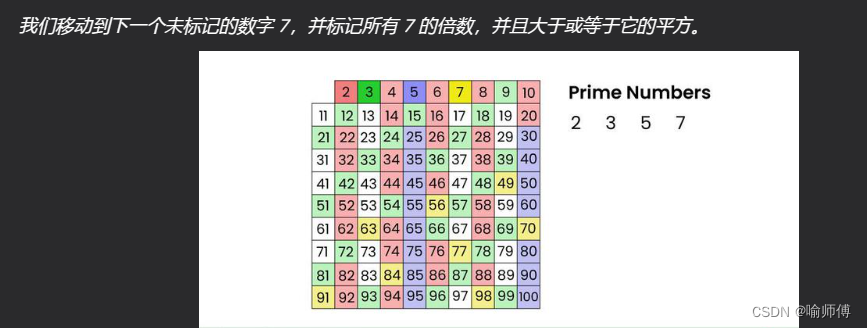
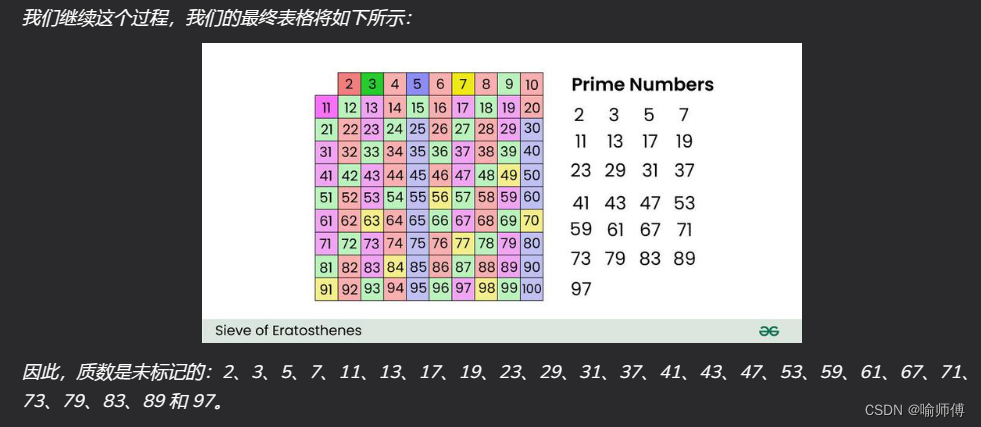

代码实现:
Java:
// Java程序,使用埃拉托斯特尼筛法打印小于或等于n的所有素数
class SieveOfEratosthenes {
void sieveOfEratosthenes(int n)
{
// 创建一个布尔数组 "prime[0..n]" 并将所有条目初始化为true。
// 如果prime[i]最终为false,则i不是素数,否则为true。
boolean prime[] = new boolean[n + 1];
for (int i = 0; i <= n; i++)
prime[i] = true;
// 使用埃拉托斯特尼筛法
for (int p = 2; p * p <= n; p++) {
// 如果prime[p]仍然为true,则p是素数
if (prime[p] == true) {
// 更新所有p的倍数,这些倍数大于或等于p的平方,
// 且小于等于n的数已经被标记过了
for (int i = p * p; i <= n; i += p)
prime[i] = false;
}
}
// 打印所有素数
for (int i = 2; i <= n; i++) {
if (prime[i] == true)
System.out.print(i + " ");
}
}
// 主函数
public static void main(String args[])
{
int n = 30;
System.out.print("以下是小于或等于 " + n + " 的素数: ");
SieveOfEratosthenes g = new SieveOfEratosthenes();
g.sieveOfEratosthenes(n);
}
}
C++:
// 使用埃拉托斯特尼筛法打印小于或等于n的所有素数的C++程序
#include <bits/stdc++.h>
using namespace std;
void SieveOfEratosthenes(int n)
{
// 创建一个布尔数组 "prime[0..n]" 并将所有条目初始化为true。
// 如果prime[i]最终为false,则i不是素数,否则为true。
bool prime[n + 1];
memset(prime, true, sizeof(prime));
for (int p = 2; p * p <= n; p++) {
// 如果prime[p]仍然为true,则p是素数
if (prime[p] == true) {
// 更新所有p的倍数,这些倍数大于或等于p的平方,
// 且小于等于n的数已经被标记过了
for (int i = p * p; i <= n; i += p)
prime[i] = false;
}
}
// 打印所有素数
for (int p = 2; p <= n; p++)
if (prime[p])
cout << p << " ";
}
// 主函数
int main()
{
int n = 30;
cout << "以下是小于或等于 " << n << " 的所有素数:" << endl;
SieveOfEratosthenes(n);
return 0;
}
Python:
# 使用埃拉托斯特尼筛法打印小于或等于n的所有素数的Python程序
def SieveOfEratosthenes(n):
# 创建一个布尔数组 "prime[0..n]" 并将所有元素初始化为True。
# 如果prime[i]最终为False,则i不是素数,否则为True。
prime = [True for i in range(n+1)]
p = 2
while (p * p <= n):
# 如果prime[p]仍然为True,则p是素数
if (prime[p] == True):
# 更新所有p的倍数
for i in range(p * p, n+1, p):
prime[i] = False
p += 1
# 打印所有素数
for p in range(2, n+1):
if prime[p]:
print(p)
# 主函数
if __name__ == '__main__':
n = 20
print("以下是小于或等于 {} 的素数:".format(n))
SieveOfEratosthenes(n)
为什么埃拉托斯特尼筛法只需要从每个素数的平方开始标记?
- 因为小于 (p^2) 的数,如果它们是合数,已经被之前的素数标记过了。
- 这样做可以确保每个合数只被标记一次,提高算法的效率。
示例:
-
初始化: 创建一个布尔数组
is_prime,长度为n+1,其中n是我们要找出的最大素数的范围。数组中的每个元素都初始化为True,表示该索引对应的数是素数。对于找出小于或等于 30 的所有素数,创建长度为 31 的数组。
is_prime = [True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True] -
筛选过程: 开始从第一个素数 2 开始筛选。
-
素数 2 是第一个素数,我们从 (2^2 = 4) 开始,将所有大于等于 4 的偶数标记为
False,因为它们都可以被 2 整除。具体操作是将数组中索引为 4、6、8、10、12、… 的位置置为False。is_prime = [True, True, True, True, False, True, False, True, False, True, False, True, False, True, False, True, False, True, False, True, False, True, False, True, False, True, False, True, False, True, False] -
接下来,选择下一个未被标记为
False的数,即素数 3,因为小于 (3的平方) 的数,如果它们是合数,已经被之前的素数标记过了,所以直接从 (3^2 = 9) 开始,标记所有大于等于 9 的数中可以被 3 整除的数为False。is_prime = [True, True, True, True, False, True, False, True, False, False, False, True, False, True, False, False, False, True, False, True, False, False, False, True, False, False, False, True, False, True, False] -
继续这个过程,选择下一个未被标记为
False的数,即素数 5,从 (5^2 = 25) 开始,标记所有大于等于 25 的数中可以被 5 整除的数为False。is_prime = [True, True, True, True, False, True, False, True, False, False, False, True, False, True, False, False, False, True, False, True, False, False, False, True, False, False, False, True, False, True, False]
-
-
提取素数: 最终,所有仍为
True的索引位置(除了 0 和 1)表示素数。素数是 2、3、5、7、11、13、17、19、23、29。