前言
本章我们继续了解二叉树。上文我们对树和二叉树有了简单的了解,详见二叉树(一)

这里我要解释一下为什么我们不对树进行增删查改呢?答案是:没有意义。我们更应该把有限的精力用作有意的地方,那么我们今天将对二叉树对有个更深的理解。
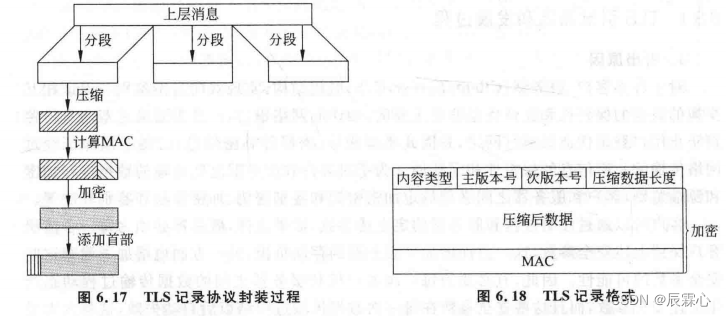
二叉树的一般用左孩子右兄弟实现代码:
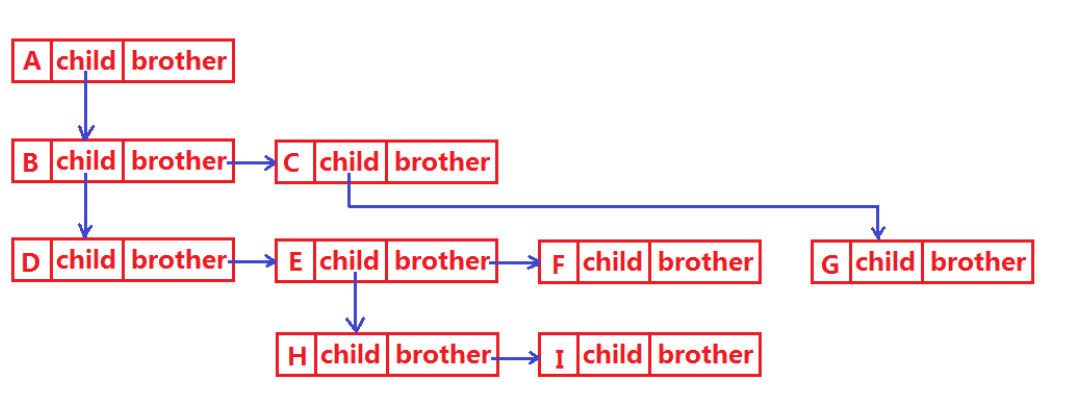
左孩子右兄弟原理图
树的理解
我们先来复习一下上节的知识,判断树与非树。
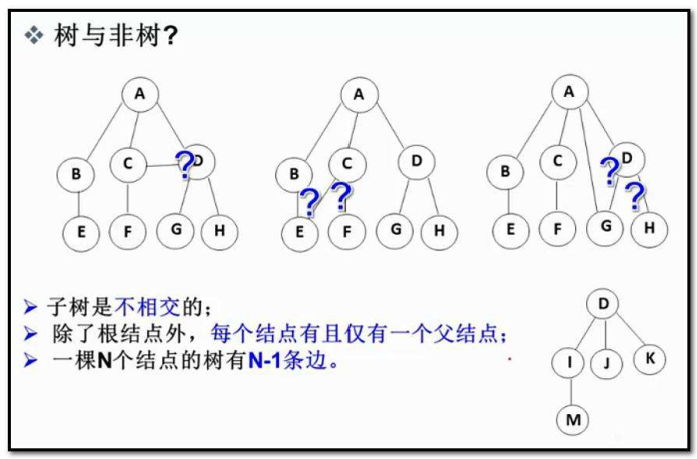
这些显然不是。(这些结构可能带环,数据结构为图)
特殊的二叉树
下图在普通人眼里是一个很普通的树,但是在程序员眼中是一个标准的二叉树,而且是满二叉树。

这一幅图就没那么标准了。

接下来我们再来了解二叉树中的特殊情况。
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉
树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。

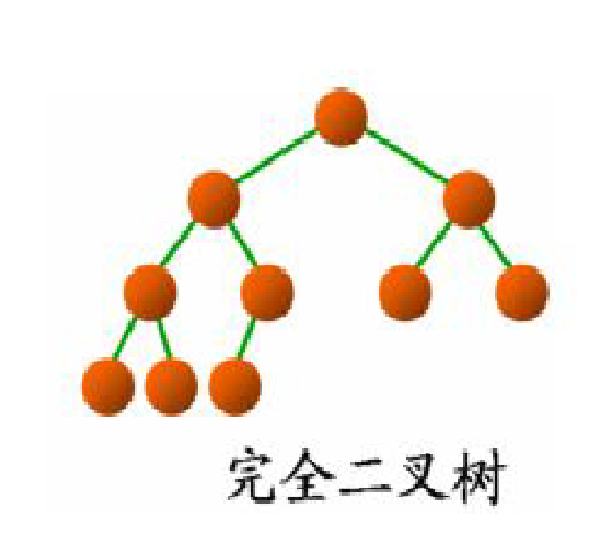
完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对
于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号
从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉
树。
假 设 树 的 高 度 是 h
1 、 前 h 一 1 层 都 是 满 的
2 、 最 后 一 层 不 满 , 但 是 最 后 一 层 从 左 往 右 都 是 连 续 的
显然我们的实物图就是——满二叉树。
二叉树的性质
我们仔细观察下图:

我们会发现有许多数学性质:
每层都是满的
假设树的高度为h,那么总结点数N为2*h-1
总结点数怎么来的呢?我们可以在百度查一下等比数列求和公式Sn=a1 (1-q^n)
有了公式我们就能很快地求导出总结点数的规律了。
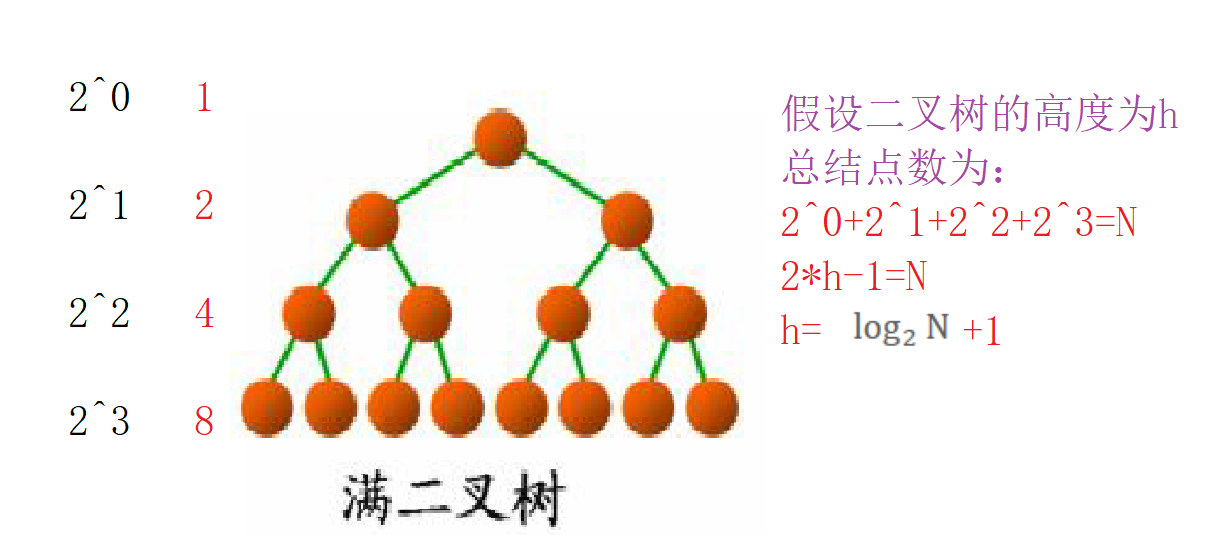
节点数规律
搜索二叉树
之前我们讲过普通的二叉树的增删查改没有意义,但是搜索二叉树却不同。
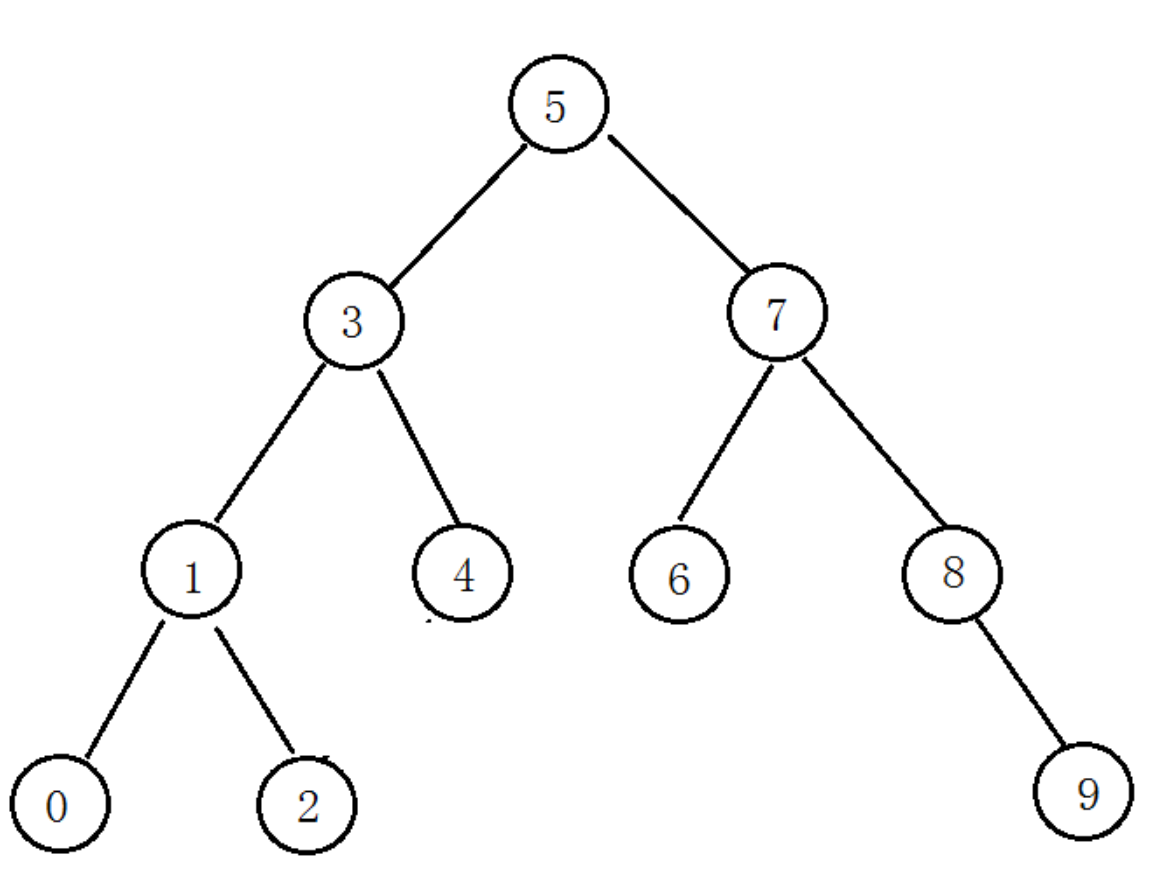
搜索二叉树
规律:任何一颗树,左子树都比根要小,右子树都比根要大
搜索中查找一个,最多查找高度次数(时间复杂度):O(N)
最复杂的情况:
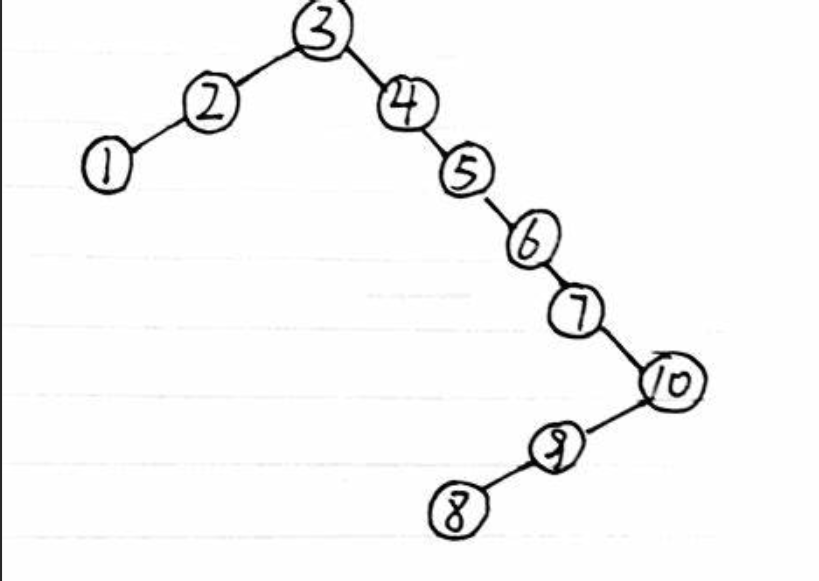
一般来说,左右两边的节点数据比较均匀
但是这里就涉及到了,平衡树,AVL树和红黑树
二叉树的性质
这些性质对做题有比较大的帮助。
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h- 1.
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0=n2
+1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=LogN
练习:
某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为()
A 不存在这样的二叉树
B200
C198
D199
解析:这里直接199+1,不知道的直接看一下前面的定义。
总结
本节首先回顾了树和二叉树的性质,然后详细了解了特殊二叉树的性质,虽然没有具体到代码,但是我相信对概念的理解比代码本身更加重要,二叉树本身是一个很难理解的概念,一两节课是讲不完的,我们要对学好二叉树下好足够的功夫的准备,不能好高骛远。
欢迎大家点赞和评论哦!