在 一道全等三角形几何证明题 的最后我使用反证法获得了解法三,但只是稍微提到了自由度,本文详细说一下,然后下一篇文章给出我的一个求最小生成树的新方法,同样基于自由度和反证法。
再次给出那道几何题,并给出一些话:
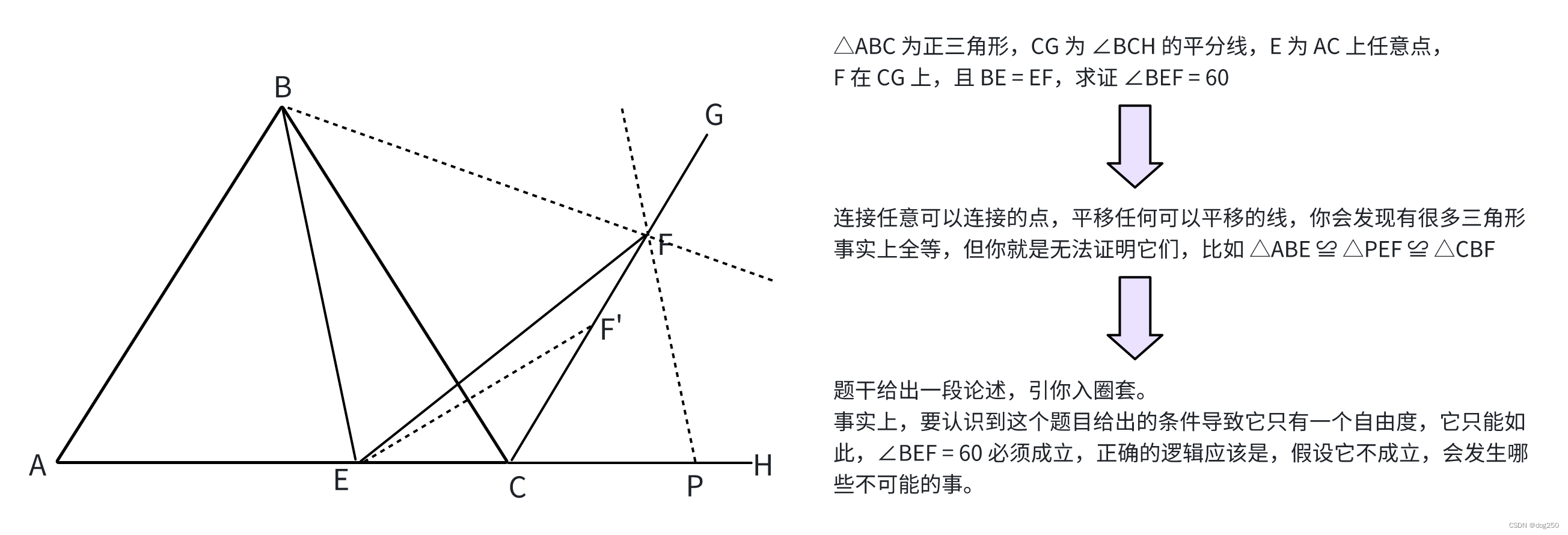
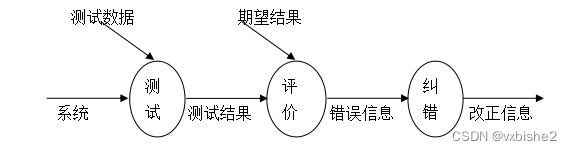
作 EF’ = EF,让 ∠BEF’ ≠ 60,显然可以导出不可能的结论 ∠EF’C > ∠GCH,这意味着 F’ 必须和 F 重合,∠BEF = 60.
这里面最重要的是,∠ECF > 90,导致 EF = L(L 为常数),是唯一的,因为若不是如此,∠EF’C 将 > 90 < ∠FCH,即 “钝角 < 锐角”。但如果 ∠ECF < 90,“钝角 < 钝角” 却是可能成立的:
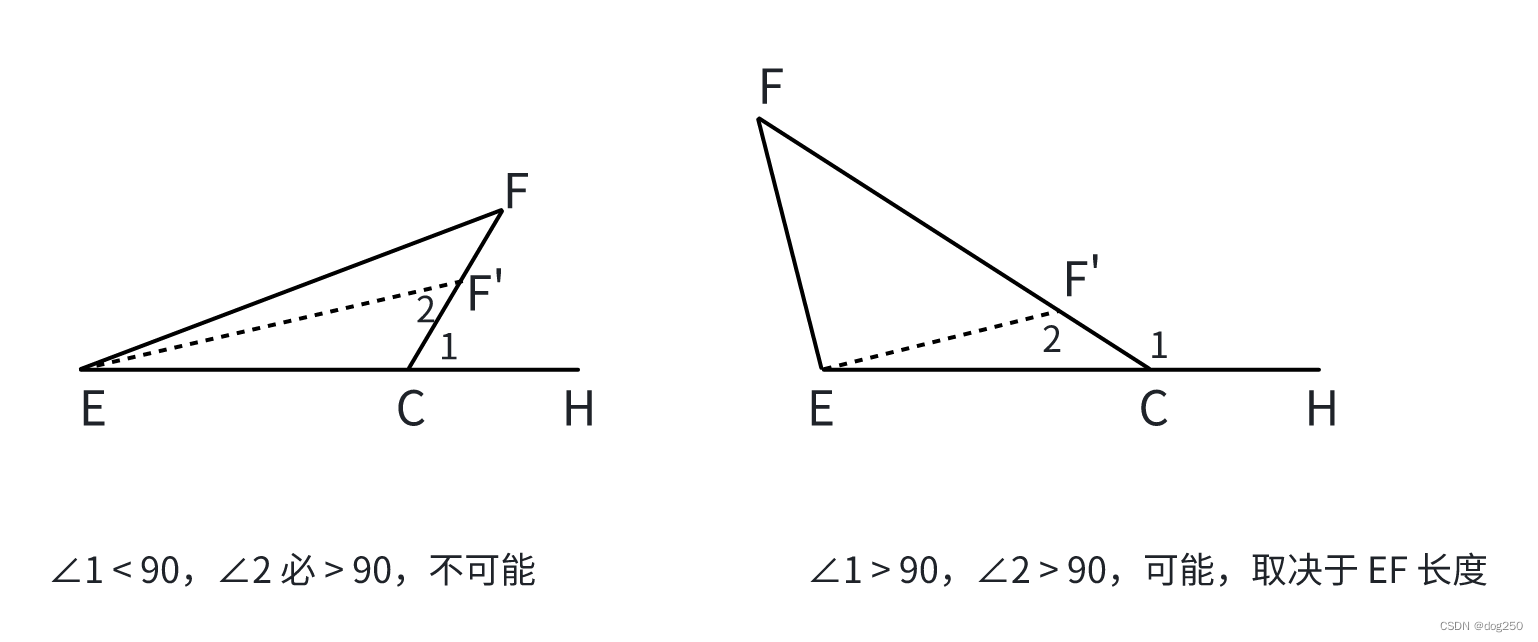
事实上,这道题确定了 ∠FCH = 120,木架子就钉死了,只有一种钉法。
再看最小生成树的 kruskal 算法,同样,无论你怎么试,结果都是正确的,但你很难通过穷举法去证明算法的正确性,同样的思路,既然它是唯一的(特指步骤唯一,并非说最小生成树唯一,最小生成树并不唯一),那就假设不这样会如何。
假设 G’ 是客观上存的那棵最小生成树,而 G 是用 kruskal 算法构造的树,如果它们不是同一棵树,至少有一条边属于 G 而不属于 G’,我们假设第一条这样的边就是按照 kruskal 算法加入 G 的当前边 e,言外之意是小于 e 的边如果在 G 中,也一定在 G’ 中,反之亦然,现在将 e 加入 G’,显然会构成一个环,现在用这个环推出一个不可能的事。
在这个环中删除一条不同于 e 的边 e’,构成一棵新的树 G’‘,如果 W(e’) > W(e),则新树 G’’ 的总权重更小,与 G’ 是客观的最小生成树矛盾,如果 W(e’) < W(e),则说明 G 在构造过程中先于 e 加入 e’ 时出现了环,因此 e’ 未加入 G,但根据假设,W 小于 e 的边如果在 G,一定在 G’,如果不在 G,也一定不在 G’,因此 e’ 不在 G’,而这纯属无中生有:
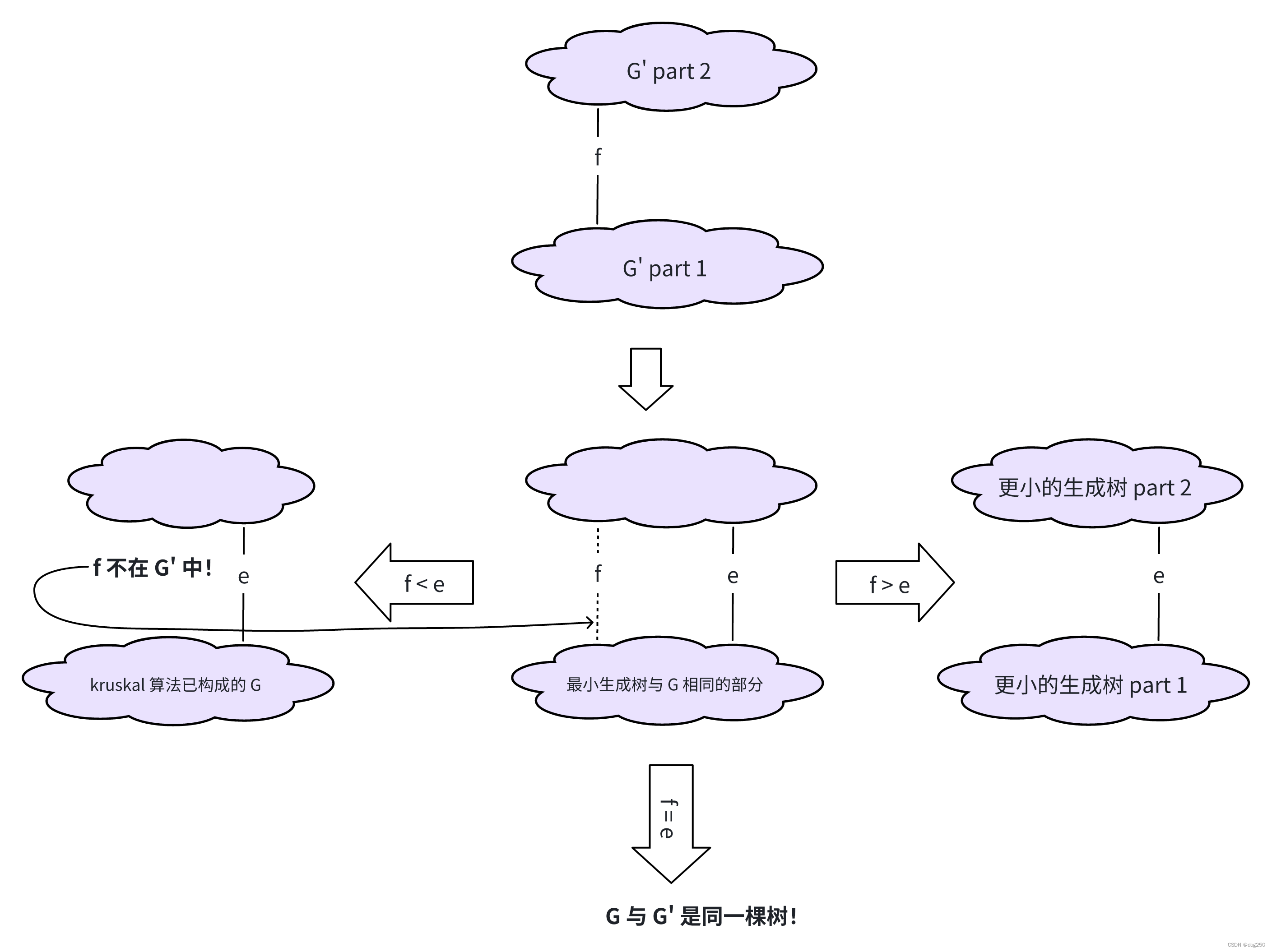
kruskal 算法的执行过程基本就把架子钉死了,但你却很难正面说明每一个细节,反之,说明不这样会如何就很容易,最终只能信任照着算法描述的步骤生成最小生成树,它一定是正确的。
反证法是纯逻辑演绎,而像教科书里全等三角形的习题则属于给你个锤子让你找钉子,和逻辑无关,我称之为贱题。虽然这些贱锤子本身也是反证法得来的,可大部分只会背诵 sas,asa,sss,hl…却根本证明不了这些结论,为什么三条边相等,两个三角形就全等,因为不相等不行啊,它没多余的自由度啊,木工都懂。
浙江温州皮鞋湿,下雨进水不会胖。