时间复杂度的相关概念

news2025/2/27 18:14:24

1. 统计时间增长趋势

时间复杂度分析统计的不是算法运行时间，而是算法运行时间随着数据量变大时的增长趋势，也就是算法运行时间与输入数据的关系。

// 算法 A 的时间复杂度：常数阶
function algorithm_A(n) {
  console.log(0);
}
// 算法 B 的时间复杂度：线性阶
function algorithm_B(n) {
  for (let i = 0; i < n; i++) {
    console.log(0);
  }
}
// 算法 C 的时间复杂度：常数阶
function algorithm_C(n) {
  for (let i = 0; i < 1000000; i++) {
    console.log(0);
  }
}

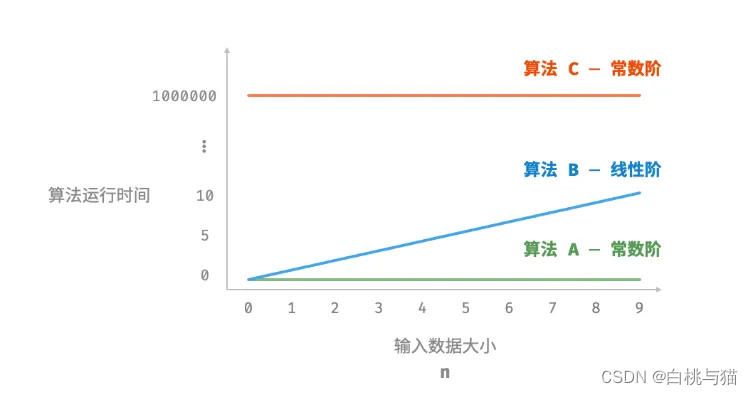
● 算法 A 只有 1 个打印操作，算法运行时间不随着 n 增大而增长。我们称此算法的时间复杂度为“常数阶”。
● 算法 B 中的打印操作需要循环 n 次，算法运行时间随着 n 增大呈线性增长。此算法的时间复杂度被称为“线性阶”。
● 算法 C 中的打印操作需要循环 1000000 次，虽然运行时间很长，但它与输入数据大小 n 无关。因此 C 的时间复杂度和 A 相同，仍为“常数阶”。
在这里插入图片描述

2. 函数渐近上界

function algorithm(n) {
    var a = 1; // +1
    a += 1; // +1
    a *= 2; // +1
    // 循环 n 次
    for(let i = 0; i < n; i++){ // +1（每轮都执行 i ++）
        console.log(0); // +1
    }
}

设算法的操作数量是一个关于输入数据大小 n 的函数，记为 $T (n)$ ，则以上函数的操作数量为： $T (n) = 3 + 2 n$
$T (n)$ 是一次函数，说明其运行时间的增长趋势是线性的，因此它的时间复杂度是线性阶。
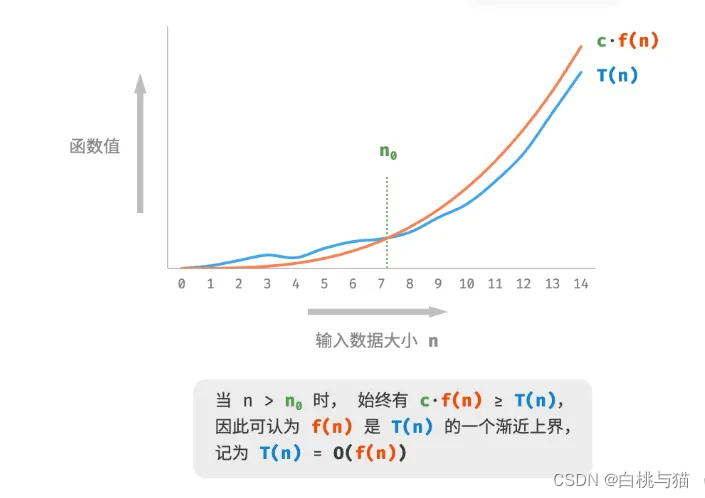
我们将线性阶的时间复杂度记为 $O (n)$ ，这个数学符号称为大 O 记号（big-O notation），表示函数 $T (n)$ 的渐近上界（asymptotic upper bound）。
在这里插入图片描述

所以要知道执行的时间复杂度，就是要确定 $f (n)$

3. 推算方法

步骤1: 统计操作数量 T(n)

由于上述 c⋅f(n) 中的常数项 c 可以取任意大小，因此操作数量 T(n) 中的各种系数、常数项都可以忽略，循环嵌套时使用乘法。

function algorithm(n) {
    let a = 1;  // +0（技巧 1）
    a = a + n;  // +0（技巧 1）
    // +n（技巧 2）
    for (let i = 0; i < 5 * n + 1; i++) {
        console.log(0);
    }
    // +n*n（技巧 3）
    for (let i = 0; i < 2 * n; i++) {
        for (let j = 0; j < n + 1; j++) {
            console.log(0);
        }
    }
}

所以简化后的操作数量 $T(n) = n^2+n$

步骤2：判断渐近上界

时间复杂度由 $T (n)$ 中最高阶的项来决定.
在这里插入图片描述

所以上面例子的时间复杂度为 $O(n^2)$

4. 常见的时间复杂度类型

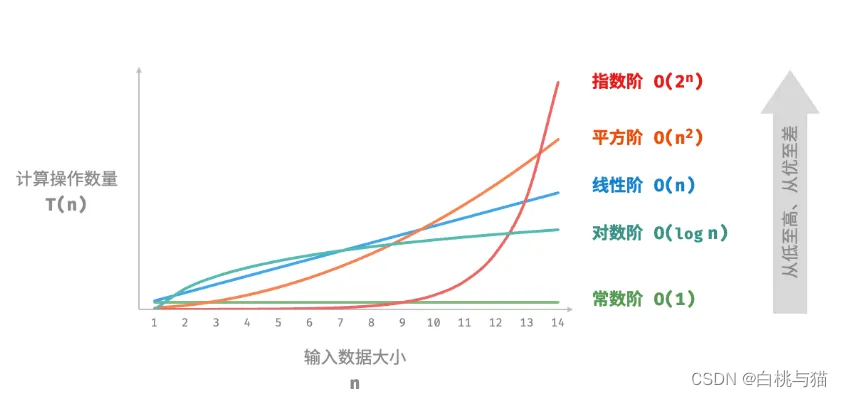
在这里插入图片描述

常数阶 O(1)

操作数量与输入数据大小n 无关

/* 常数阶 */
function constant(n) {
    let count = 0;
    const size = 100000;
    for (let i = 0; i < size; i++) count++;
    return count;
}

线性阶O(n)

操作数量取决于输入数据大小n，随着n变化

/* 线性阶 */
function linear(n) {
    let count = 0;
    for (let i = 0; i < n; i++) count++;
    return count;
}

平方阶

通常出现在内外循环中

/* 平方阶 */
function quadratic(n) {
    let count = 0;
    // 循环次数与数据大小 n 成平方关系
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < n; j++) {
            count++;
        }
    }
    return count;
}

指数阶

/* 指数阶（循环实现） */
function exponential(n) {
    let count = 0,
        base = 1;
    // 细胞每轮一分为二，形成数列 1, 2, 4, 8, ..., 2^(n-1)
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < base; j++) {
            count++;
        }
        base *= 2;
    }
    // count = 1 + 2 + 4 + 8 + .. + 2^(n-1) = 2^n - 1 = z^n
    return count;
}

对数阶

一般用于分治策略中，比如二分法。

与指数阶相反，对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为 n ，由于每轮缩减到一半，因此循环次数是 $log_2^n$ ，即 $2^n$ 的反函数。

/* 对数阶（循环实现） */
function logarithmic(n) {
    let count = 0;
    while (n > 1) {
        n = n / 2;
        count++;
    }
    return count;
}

$T(n) = log_2^n+1$
$O(n) = log_2^n$

在这里插入图片描述

所以无论底数m为多少，对其本身的时间复杂度不影响，所以通常会省略底数m。

线性对数阶

线性对数阶常出现于嵌套循环中，两层循环的时间复杂度分别为 $O(log^n)$ 和 $O (n)$

/* 线性对数阶 */
function linearLogRecur(n) {
    if (n <= 1) return 1;
    let count = linearLogRecur(n / 2) + linearLogRecur(n / 2);
    for (let i = 0; i < n; i++) {
        count++;
    }
    return count;
}

阶乘阶 O(n!)

阶乘阶对应数学上的“全排列”问题。给定 n 个互不重复的元素，求其所有可能的排列方案，方案数量为：
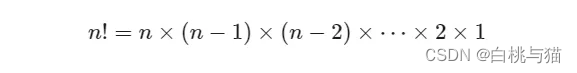
在这里插入图片描述

阶乘通常使用递归实现。

/* 阶乘阶（递归实现） */
function factorialRecur(n) {
    if (n === 0) return 1;
    let count = 0;
    // 从 1 个分裂出 n 个
    for (let i = 0; i < n; i++) {
        count += factorialRecur(n - 1);
    }
    return count;
}

5. 最差、最佳、平均时间复杂度

假设输入一个长度为 n 的数组 nums ，其中 nums 由从 1 至 n 的数字组成，每个数字只出现一次；但元素顺序是随机打乱的，任务目标是返回元素 1 的索引。我们可以得出以下结论。
● 当 nums = [?, ?, …, 1] ，即当末尾元素是 1 时，需要完整遍历数组，达到最差时间复杂度 $O (n)$
● 当 nums = [1, ?, ?, …] ，即当首个元素为 1 时，无论数组多长都不需要继续遍历，达到最佳时间复杂度 $O (1)$