欧拉函数的定义

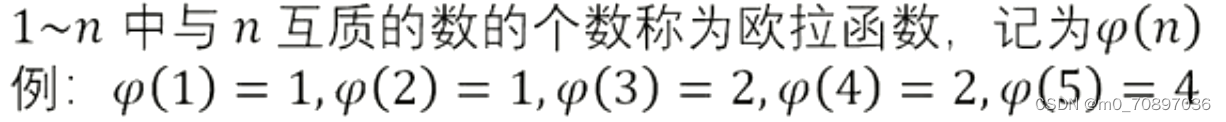
欧拉函数的性质

 

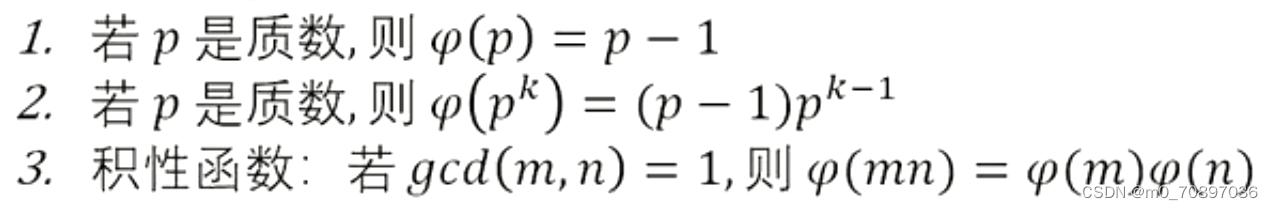
性质1是性质2的特殊情况
性质1的理解：一个数a是质数，前面的数b与a的gcd一定是1
性质2的理解：1,2,…p,p+1,p+2…2p,…3p…p^k
其中以np结尾的序列重复了p^（k-1）次，每一次的循环与p ^k互质的数都有p-1个

欧拉函数计算公式

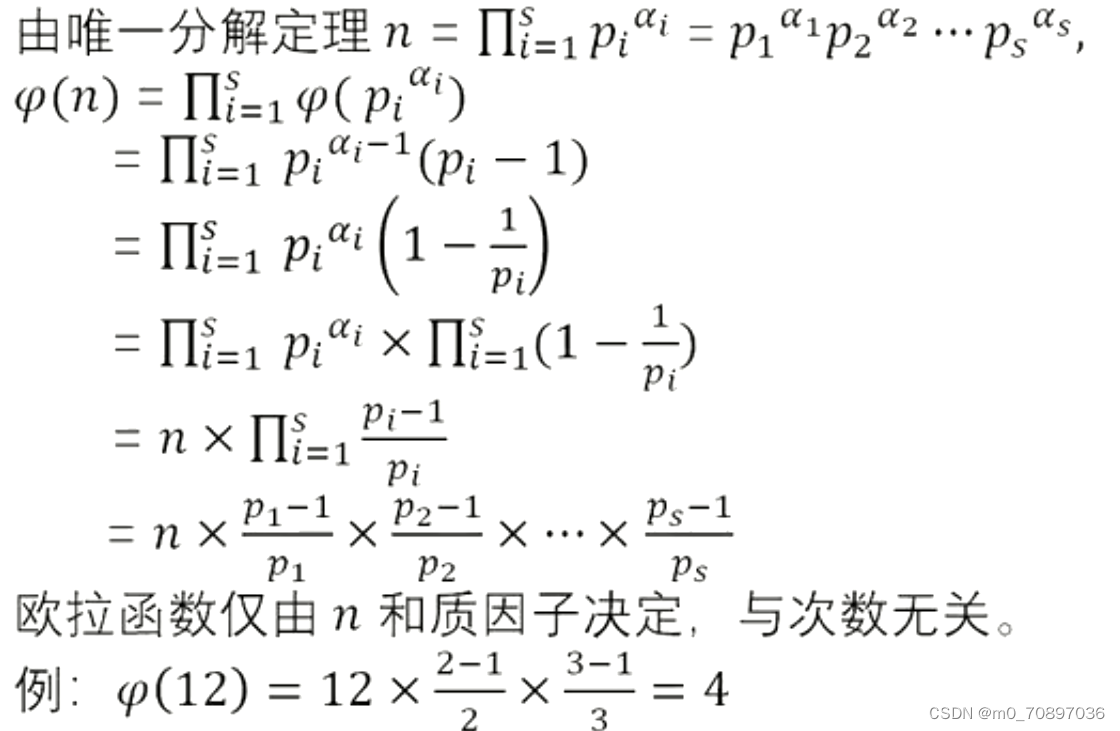
试除法求欧拉函数

int phi(int n)
{
	int res=n;
	for(int i=2;i<=sqrt(n);i++)
	{
		if(n%i==0)
		{
			res=res/i*(i-1);
			while(n%i==0)n/=i;//卸掉所有的当前因子i 
		}
	}
	if(n>1)res=res/n*(n-1); 
	return res;
}

示例

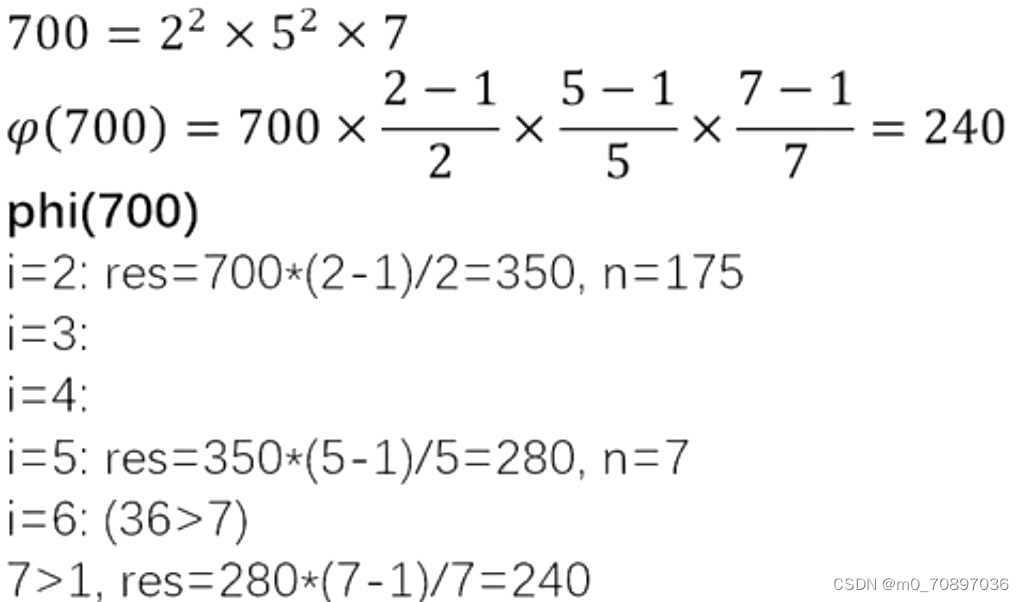
筛法求欧拉函数

筛法求欧拉函数实在筛法求素数的过程中同步进行的，关于线性筛求素数见>判断素数的方法<

#define MAX_N 10000
int cnt=0;
int prim[MAX_N+5];
int vis[MAX_N+5];
int phi[MAX_N+5];
void get_phi(int n)
{
	phi[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!vis[i])
		{
			phi[i]=i-1;
			prim[++cnt]=i;
		}
		for(int j=1;prim[j]*i<=n;j++)
		{
			int m=i*prim[j];
			vis[m]=1;
			if(i%prim[j]==0)
			{
				phi[m]=prim[j]*phi[i];
				break;//避免重复记录合数
			}
			else{
				phi[m]=(prim[j]-1)*phi[i];
			}
		}	
	}
	return ;
}

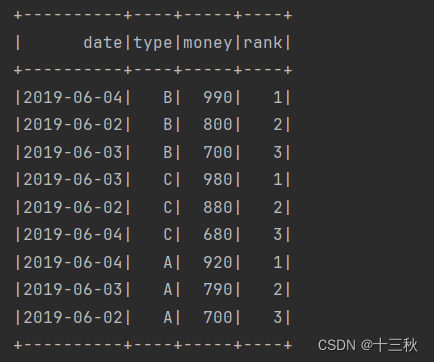
示例

>欧拉函数练习题<