Take it easy!

2024年6月19日

---

题目描述

        假设有n个活动和一个资源，每个活动执行时都需要占用该资源，并且该资源在任何时间只能被一个活动所占用，一旦某个活动开始执行，中间将不能被打断，直到其执行完毕。每个活动i都有一个开始时间start_i和结束时间end_i（start_i < end_i），其占用的资源的时间=start_i - end_i。假设最早活动执行的时间为0，试求一种最优活动安排方案，使得安排的活动占用时间最长。

输入格式

        第一行输入t表示活动的数量，其后的t行分别输入每个活动的开始时间和结束时间。

输入样例

11

1   4
3   5
6   10
0   6
5   7
3   8
8   12
5   9
8   11
12  15
2   13

输出样例

13

---

题解方法

        贪心法+动态规划

1. 根据贪心思想，按活动结束时间递增排序；

2. 确定状态转移方程；（本题和0-1背包问题类似）

dp[i]表示在活动0~i之间选取可兼容的活动能够持续的最长时间。

• 和0-1背包问题有一点相似，每个活动都有选与不选，但是需要确定每个活动的前驱活动；（注意前驱活动不是想当然的前一个活动！前驱活动表示与当前活动相兼容的前一个活动）
• 如果没有前驱活动，当前dp[i] = max(dp[i - 1], v[i].end - v[i].start)；
• 如果有前驱活动，当前dp[i] = max(dp[i - 1], dp[j] + v[i].end - v[i].start)；

题解代码

1. 定义活动结构体；

struct Action{
    int start;
    int end;
    Action(int start, int end):start(start), end(end) {}
    bool operator<(const Action &a) const{
        return end <= a.end;
    }
};

2. 定义求解最长持续时间函数；

int getLongestLastTime(vector<Action> &v, vector<int> &dp){
    sort(v.begin(), v.end());
    int len = v.size();
    // 定义结果
    int res = 0;
    // 第一个活动很明显没有前驱活动
    // dp[i]表示在0~i之间的活动中选取，持续的最长时间
    dp[0] = v[0].end - v[0].start;
    for(int i = 1; i < len; i++){
        // 定义前驱活动的标记
        int pre = i - 1;
        while(pre >= 0 && v[pre].end > v[i].start){
            pre--;
        }
        if(pre != -1){//说明有前驱活动
            dp[i] = max(dp[i-1], dp[pre] + v[i].end - v[i].start);
        }
        else{
            dp[i] = max(dp[i-1], v[i].end - v[i].start);
        }
    }
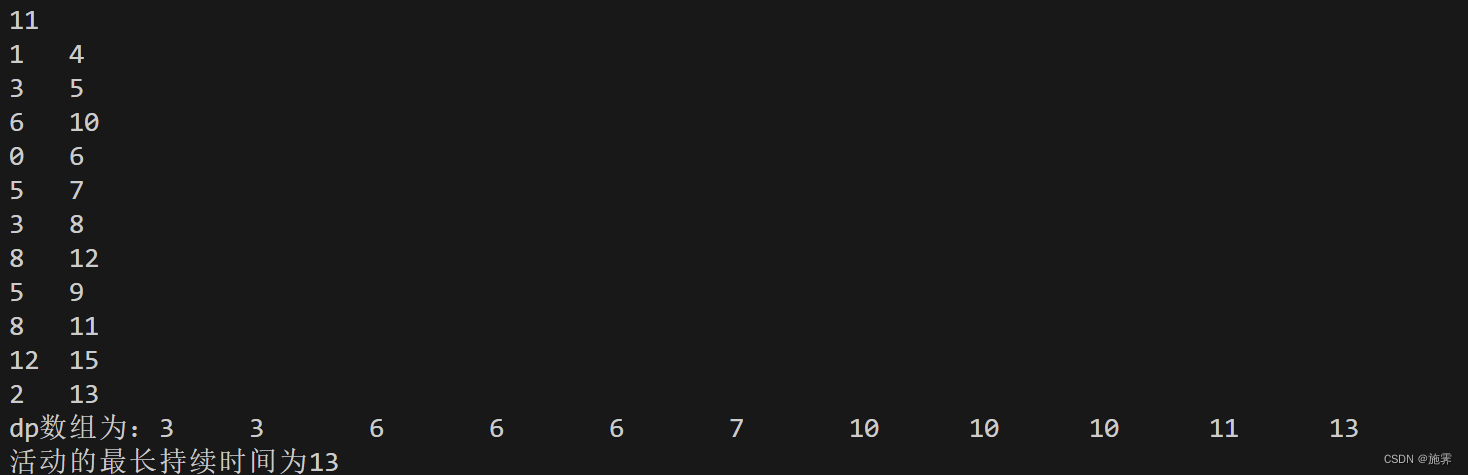
    cout<<"dp数组为：";
    for(auto e:dp){
        cout<<e<<'\t';
    }
    return dp[len-1];
}

3. 完整代码

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

struct Action{
    int start;
    int end;
    Action(int start, int end):start(start), end(end) {}
    bool operator<(const Action &a) const{
        return end <= a.end;
    }
};

int getLongestLastTime(vector<Action> &v, vector<int> &dp){
    sort(v.begin(), v.end());
    int len = v.size();
    // 定义结果
    int res = 0;
    // 第一个活动很明显没有前驱活动
    // dp[i]表示在0~i之间的活动中选取，持续的最长时间
    dp[0] = v[0].end - v[0].start;
    for(int i = 1; i < len; i++){
        // 定义前驱活动的标记
        int pre = i - 1;
        while(pre >= 0 && v[pre].end > v[i].start){
            pre--;
        }
        if(pre != -1){//说明有前驱活动
            dp[i] = max(dp[i-1], dp[pre] + v[i].end - v[i].start);
        }
        else{
            dp[i] = max(dp[i-1], v[i].end - v[i].start);
        }
    }
    cout<<"dp数组为：";
    for(auto e:dp){
        cout<<e<<'\t';
    }
    return dp[len-1];
}

int main(){

    vector<Action> v;
    int t;
    cin>>t;
    for(int i = 0; i < t; i++){
        int start, end;
        cin>>start>>end;
        v.push_back(Action(start, end));
    }

    vector<int> dp(v.size(), 0);
    int res = getLongestLastTime(v, dp); 
    cout<<endl<<"活动的最长持续时间为"<<res;
    return 0;
}

4. 输出结果