27 map和set封装

news2025/2/22 11:35:19

map和set可以采用两套红黑树实现，也可以用同一个红黑树，就需要对前面的结构进行修改
迭代器的好处是可以方便遍历，是数据结构的底层实现与用户透明。如果想要给红黑树增加迭代器，需要考虑以前问题：

  • begin()和end()

stl明确规定，begin和edn代表的是一段前闭后开的区间，而对红黑树进行中序遍历后，可以得到一个有序序列，因此：begin可以放在红黑树中最小节点（即最左侧节点）的位置，end放在最大结点（最右侧节点）的下一个位置，关键是最大节点的下一个位置在哪？如果给成nullptr，end的–操作要能找到最后一个元素的位置，最好的方式是将end放在头节点的位置

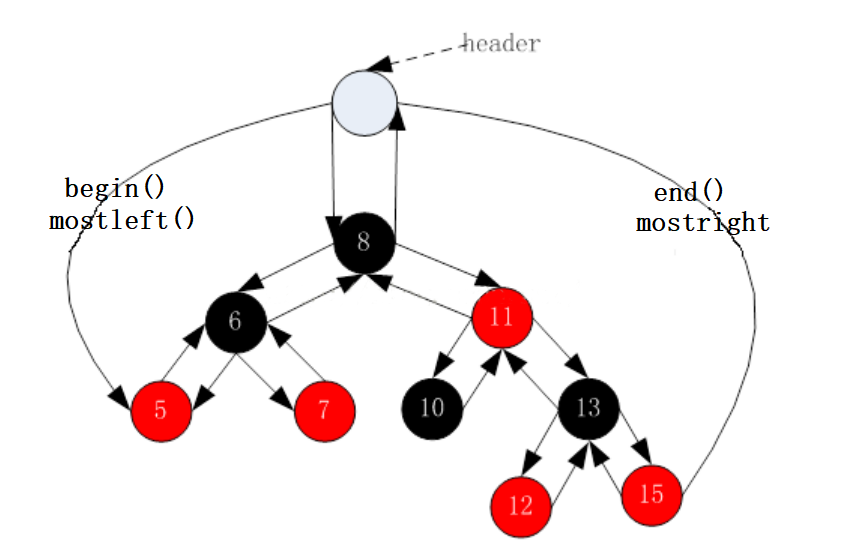
在这里插入图片描述

迭代器结构

在红黑树中提供一个迭代器类，提供基本的*，->，++，–等运算符重载。变量时一个节点指针，用节点来初始化迭代器
在这里插入图片描述
加入上面构造的好处
固定的普通迭代器初始化这个迭代器类，参数模板都用T，如果T传入的是普通迭代器，就是拷贝构造，如果是cosnt迭代器，就支持用普通迭代器隐式转换常量迭代器，保证set的key不能修改

++和–

迭代器的++是按中序遍历的顺序找到下一个元素，遵循中序的原则。规则是：当前节点判断它的右节点有没有节点，如果有，就找到右子树中最小的，也就是最左的结点。如果是空，就看它是双亲的左还是右，如果是左，按中序原则就到它的父亲位置，如果是右，说明这颗子树遍历完毕，向上重复直到找到cur是par的左节点的时候，如果到end的位置就结束

self& operator++()
{
	//1.右不为空,找右树最左节点
	if (_node->_right != nullptr)
	{
		node* subleft = _node->_right;
		while (subleft->_left)
		{
			subleft = subleft->_left;
		}

		_node = subleft;
	}
	else
	{
		//2.右为空,沿着路径找孩子是父亲左的祖先
		node* cur = _node;
		node* parent = cur->_parent;
		while (parent && parent->_right == cur)
		{
			cur = parent;
			parent = parent->_parent;
		}

		_node = parent;
	}

	return *this;
}

–和++的操作是镜像的，左为空，找是右子树的结点

self& operator--()
{
	//1.左不为空,找左树最右节点
	if (_node->_left != nullptr)
	{
		node* subright = _node->_left;
		while (subright->_right)
		{
			subright = subright->_right;
		}

		_node = subright;
	}
	else
	{
		//2.左为空,沿着路径找孩子是父亲右的祖先
		node* cur = _node;
		node* parent = cur->_parent;
		while (parent && parent->_left == cur)
		{
			cur = parent;
			parent = parent->_parent;
		}

		_node = parent;
	}

	return *this;
}

全

enum color
{
	RED,
	BLACK
};
template <class T>
struct TreeNode
{
	struct TreeNode<T>* _parent;
	struct TreeNode<T>* _left;
	struct TreeNode<T>* _right;
	T _data;
	color _col;

	TreeNode(T data)
		:_parent(nullptr), _left(nullptr), _right(nullptr)
		, _data(data), _col(RED)
	{}
};
template <class T, class Ref, class Ptr>
struct __RBTreeIterator
{
	typedef TreeNode<T> node;
	typedef __RBTreeIterator<T, Ref, Ptr> self;
	node* _node;
	__RBTreeIterator(node* cur)
		:_node(cur)
	{}
	//普通迭代器，当迭代器是普通时是拷贝构造，是const迭代器时支持普通转换const
	__RBTreeIterator(const __RBTreeIterator<T, T&, T*>& it)
	{
		_node = it._node;
	}

	Ref operator*()
	{
		return _node->_data;
	}

	Ptr operator->()
	{
		return &_node->_data;
	}

	bool operator!=(const self& x)
	{
		return x._node != _node;
	}

	self& operator++()
	{
		//1.右不为空,找右树最左节点
		if (_node->_right != nullptr)
		{
			node* subleft = _node->_right;
			while (subleft->_left)
			{
				subleft = subleft->_left;
			}

			_node = subleft;
		}
		else
		{
			//2.右为空,沿着路径找孩子是父亲左的祖先
			node* cur = _node;
			node* parent = cur->_parent;
			while (parent && parent->_right == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}

			_node = parent;
		}

		return *this;
	}

	self& operator--()
	{
		//1.左不为空,找左树最右节点
		if (_node->_left != nullptr)
		{
			node* subright = _node->_left;
			while (subright->_right)
			{
				subright = subright->_right;
			}

			_node = subright;
		}
		else
		{
			//2.左为空,沿着路径找孩子是父亲右的祖先
			node* cur = _node;
			node* parent = cur->_parent;
			while (parent && parent->_left == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}

			_node = parent;
		}

		return *this;
	}

};

begin和end

红黑树提供begin和end功能，begin返回最左的元素，也就是最小的值。end返回空迭代器

typedef __RBTreeIterator<T, T&, T*> iterator;
typedef __RBTreeIterator<T, const T&, const T*> const_iterator;

iterator begin()
{
	//中序第一个,最左节点
	node* cur = _root;
	while (cur && cur->_left)
	{
		cur = cur->_left;
	}
	return iterator(cur);
}

const_iterator begin() const
{
	//中序第一个,最左节点
	node* cur = _root;
	while (cur && cur->_left)
	{
		cur = cur->_left;
	}
	return const_iterator(cur);
}

iterator end()
{
	return iterator(nullptr);
}

const_iterator end() const
{
	return const_iterator(nullptr);
}

insert返回值

insert的返回值返回pair，第一个参数是iterator，第二个参数插入成功或失败，如果插入成功，就返回插入位置，插入失败，就返回已经存在的数据位置

insert比较

set是比较key的值，而map传入的值是pair，pair本身的比较规则是先比较first，first相等比较second。而我们想要的是只比较first，所以要统一两个的比较方法
在这里插入图片描述
在这里插入图片描述

模板里传入一个KeyOfT，是一个仿函数，根据不同的T的类型，取到set和map用于比较的元素

std::pair<iterator, bool> insert(const T& data)
{
	KeyOfT kot;
	if (_root == nullptr)
	{
		_root = new node(data);
		_root->_col = BLACK;
		return std::make_pair(iterator(_root), true);
	}

	node* parent = nullptr;
	node* cur = _root;
	while (cur)
	{
		parent = cur;
		if (kot(data) < kot(cur->_data))
		{
			cur = cur->_left;
		}
		else if (kot(data) > kot(cur->_data))
		{
			cur = cur->_right;
		}
		else
		{
			return std::make_pair(iterator(cur), false);;
		}
	}
	//插入
	cur = new node(data);
	node* newnode = cur;
	cur->_parent = parent;
	if (data < parent->_data)
	{
		parent->_left = cur;
	}
	else
	{
		parent->_right = cur;
	}

	//父节点是红色调整
	while (parent && parent->_col == RED)
	{
		node* gdparent = parent->_parent;
		node* uncle;

		if (gdparent->_left == parent)
		{
			uncle = gdparent->_right;
			//第一种情况 叔叔节点是红色,变色
			if (uncle && uncle->_col == RED)
			{
				parent->_col = uncle->_col = BLACK;
				gdparent->_col = RED;
			}
			//第二种情况 分左右
			//     g
			//  par  un
			// cur
			else
			{
				if (cur == parent->_left)
				{
					RotateRight(gdparent);
					parent->_col = BLACK;
					gdparent->_col = RED;
				}
				//     g
				//  par  un
				//    cur
				else
				{
					RotateLeft(parent);
					RotateRight(gdparent);
					cur->_col = BLACK;
					parent->_col = RED;
					gdparent->_col = RED;
				}

				break;
			}
		}
		else
		{
			uncle = gdparent->_left;
			if (uncle && uncle->_col == RED)
			{
				parent->_col = uncle->_col = BLACK;
				gdparent->_col = RED;
			}
			else
			{
				if (cur == parent->_right)
				{
					RotateLeft(gdparent);
					parent->_col = BLACK;
					gdparent->_col = RED;
				}
				//     g
				//  par  un
				//    cur
				else
				{
					RotateRight(parent);
					RotateLeft(gdparent);
					cur->_col = BLACK;
					//parent->_col = RED;
					gdparent->_col = RED;
				}

				break;
			}
		}

		cur = gdparent;
		parent = cur->_parent;
	}

	//根必须是黑色
	_root->_col = BLACK;
	return std::make_pair(iterator(newnode), true);;
}

set和map的仿函数如下：

struct SetOfK
{
	const K& operator()(const K& key)
	{
		return key;
	}
};

struct SetOfV
{
	const K& operator()(const std::pair<const K, V>& kv)
	{
		return kv.first;
	}
};

全

#pragma once
#include <iostream>
#include <assert.h>
#include <queue>

template <class K, class T, class KeyOfT>
class RBTree
{
	typedef TreeNode<T> node;
public:
	typedef __RBTreeIterator<T, T&, T*> iterator;
	typedef __RBTreeIterator<T, const T&, const T*> const_iterator;

	iterator begin()
	{
		//中序第一个,最左节点
		node* cur = _root;
		while (cur && cur->_left)
		{
			cur = cur->_left;
		}
		return iterator(cur);
	}

	const_iterator begin() const
	{
		//中序第一个,最左节点
		node* cur = _root;
		while (cur && cur->_left)
		{
			cur = cur->_left;
		}
		return const_iterator(cur);
	}

	iterator end()
	{
		return iterator(nullptr);
	}

	const_iterator end() const
	{
		return const_iterator(nullptr);
	}

	node* find(const K& key)
	{
		KeyOfT kot;
		if (_root == nullptr)
		{
			return nullptr;
		}

		node* cur = _root;
		while (cur)
		{
			if (kot(key) < kot(cur->_data))
			{
				cur = cur->_left;
			}
			else if (kot(key) > kot(cur->_data))
			{
				cur = cur->_right;
			}
			else
			{
				return cur;
			}
		}

		return nullptr;
	}

	std::pair<iterator, bool> insert(const T& data)
	{
		KeyOfT kot;
		if (_root == nullptr)
		{
			_root = new node(data);
			_root->_col = BLACK;
			return std::make_pair(iterator(_root), true);
		}

		node* parent = nullptr;
		node* cur = _root;
		while (cur)
		{
			parent = cur;
			if (kot(data) < kot(cur->_data))
			{
				cur = cur->_left;
			}
			else if (kot(data) > kot(cur->_data))
			{
				cur = cur->_right;
			}
			else
			{
				return std::make_pair(iterator(cur), false);;
			}
		}
		//插入
		cur = new node(data);
		node* newnode = cur;
		cur->_parent = parent;
		if (data < parent->_data)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}

		//父节点是红色调整
		while (parent && parent->_col == RED)
		{
			node* gdparent = parent->_parent;
			node* uncle;

			if (gdparent->_left == parent)
			{
				uncle = gdparent->_right;
				//第一种情况 叔叔节点是红色,变色
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					gdparent->_col = RED;
				}
				//第二种情况 分左右
				//     g
				//  par  un
				// cur
				else
				{
					if (cur == parent->_left)
					{
						RotateRight(gdparent);
						parent->_col = BLACK;
						gdparent->_col = RED;
					}
					//     g
					//  par  un
					//    cur
					else
					{
						RotateLeft(parent);
						RotateRight(gdparent);
						cur->_col = BLACK;
						parent->_col = RED;
						gdparent->_col = RED;
					}

					break;
				}
			}
			else
			{
				uncle = gdparent->_left;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					gdparent->_col = RED;
				}
				else
				{
					if (cur == parent->_right)
					{
						RotateLeft(gdparent);
						parent->_col = BLACK;
						gdparent->_col = RED;
					}
					//     g
					//  par  un
					//    cur
					else
					{
						RotateRight(parent);
						RotateLeft(gdparent);
						cur->_col = BLACK;
						//parent->_col = RED;
						gdparent->_col = RED;
					}

					break;
				}
			}

			cur = gdparent;
			parent = cur->_parent;
		}

		//根必须是黑色
		_root->_col = BLACK;
		return std::make_pair(iterator(newnode), true);;
	}

	void RotateLeft(node* parent)
	{
		node* sub = parent->_right;
		node* subl = sub->_left;

		sub->_left = parent;
		parent->_right = subl;

		//父节点修改
		node* Pparent = parent->_parent;
		parent->_parent = sub;
		//有子节点改变指向
		if (subl)
		{
			subl->_parent = parent;
		}

		if (parent == _root)
		{
			_root = sub;
		}
		else
		{
			//原parent在父节点的左右
			if (Pparent->_left == parent)
			{
				Pparent->_left = sub;
			}
			else
			{
				Pparent->_right = sub;
			}
		}

		sub->_parent = Pparent;

	}

	void RotateRight(node* parent)
	{
		node* sub = parent->_left;
		node* subr = sub->_right;

		sub->_right = parent;
		parent->_left = subr;

		if (subr)
		{
			subr->_parent = parent;
		}

		node* Pparent = parent->_parent;
		parent->_parent = sub;

		if (parent == _root)
		{
			_root = sub;
		}
		else
		{
			if (Pparent->_left == parent)
			{
				Pparent->_left = sub;
			}
			else
			{
				Pparent->_right = sub;
			}
		}

		sub->_parent = Pparent;
	}

	bool IsBalance()
	{
		if (_root->_col == RED)
		{
			std::cout << "根节点是红色" << std::endl;
			return false;
		}

		int refVal = 0;  //记录最左路径黑色节点的数量,用来参考
		node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
			{
				refVal++;
			}

			cur = cur->_left;
		}

		return _IsBalance(_root, 0, refVal);
	}

	bool _IsBalance(node* cur, int blackNum, int refVal)
	{
		if (cur == nullptr)
		{
			//判断每条路径黑色节点数量正常
			if (blackNum != refVal)
			{
				std::cout << "黑色节点数量不相等" << std::endl;
				return false;
			}
			return true;
		}

		if (cur->_col == BLACK)
		{
			blackNum++;
		}

		if (cur->_col == RED && cur->_parent->_col == RED)
		{
			std::cout << cur->_kv.first << " 连续红色节点" << std::endl;
		}

		return _IsBalance(cur->_left, blackNum, refVal)
			&& _IsBalance(cur->_right, blackNum, refVal);
	}

	void layer()
	{
		if (_root == nullptr)
		{
			return;
		}

		std::queue<node*> q;
		q.push(_root);
		int lay = 1;

		while (!q.empty())
		{
			std::cout << "第" << lay << "层: ";
			int num = q.size();
			while (num--)
			{
				node* cur = q.front();
				q.pop();
				std::cout << cur->_kv.first << " 颜色:" << cur->_col << "  ";
				if (cur->_left != nullptr)
				{
					q.push(cur->_left);
				}
				if (cur->_right != nullptr)
				{
					q.push(cur->_right);
				}
			}

			lay++;
			std::cout << std::endl;
		}
		std::cout << std::endl;
	}

	void inorder()
	{
		_inorder(_root);
		std::cout << std::endl;
	}
	void _inorder(node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_inorder(root->_left);
		std::cout << root->_kv.first << " ";
		_inorder(root->_right);
	}

	int size()
	{
		return _size(_root);
	}

	int _size(node* node)
	{
		if (node == nullptr)
		{
			return 0;
		}

		return _size(node->_left) + _size(node->_right) + 1;
	}

	int TreeHeight()
	{
		return _TreeHeight(_root);
	}

	int _TreeHeight(node* node)
	{
		if (node == nullptr)
		{
			return 0;
		}

		int lhight = _TreeHeight(node->_left);
		int rhight = _TreeHeight(node->_right);

		return lhight > rhight ? lhight + 1 : rhight + 1;
	}

private:
	node* _root = nullptr;
};

set

在这里插入图片描述
两个参数都用K初始化，传入仿函数
在这里插入图片描述
普通迭代器也用const，保证key不被修改，typename用来区分是一个类还是变量类型

全

#pragma once
#include "RBTree.h"

template <class K>
class set
{
	struct SetOfK
	{
		const K& operator()(const K& key)
		{
			return key;
		}
	};

public:
	//typename 区分是类还是变量
	typedef typename RBTree<K, K, SetOfK>::const_iterator iterator;
	typedef typename RBTree<K, K, SetOfK>::const_iterator const_iterator;


	iterator begin()
	{
		return _t.begin();
	}

	iterator end()
	{
		return _t.end();
	}

	std::pair<iterator, bool> insert(const K& key)
	{
		return _t.insert(key);
	}

private:
	RBTree<K, K, SetOfK> _t;
};

map

在这里插入图片描述
map第一个是K，用来erase，find等函数接口是key，它的数据类型是pair

V& operator[](const K& key)
{
	std::pair<iterator, bool> ret = _t.insert(make_pair(key, V()));
	return ret.first->second;
}

map提供[]操作，返回key位置的值，并可以对自身修改

全

#pragma once
#include <iostream>
#include "RBTree.h"

template <class K, class V>
class map
{
	struct SetOfV
	{
		const K& operator()(const std::pair<const K, V>& kv)
		{
			return kv.first;
		}
	};

public:

	typedef typename RBTree<K, std::pair<const K, V>, SetOfV>::iterator iterator;
	iterator begin()
	{
		return _t.begin();
	}

	iterator end()
	{
		return _t.end();
	}

	std::pair<iterator, bool> insert(const std::pair<const K, V> kv)
	{
		return _t.insert(kv);
	}

	V& operator[](const K& key)
	{
		std::pair<iterator, bool> ret = _t.insert(make_pair(key, V()));
		return ret.first->second;
	}

private:
	RBTree<K, std::pair<const K, V>, SetOfV> _t;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1841090.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

ChatGPT Plus GPT-4o Claude 3 Opus合租拼车全新方式

ChatGPT Plus GPT-4o Claude 3 Opus合租拼车全新方式

无需自己搭建&#xff0c;登录即可用&#xff0c;国内直连访问&#xff0c;聚合多家最强大模型&#xff0c;随意选择使用。立即体验 datapipe.top 支持 OpenAI 最新 GPT-4o &#xff0c;获得快速高质量的对话&#xff0c;保证可用配额。支持多种大模型&#xff0c;GPT-4o &…
阅读更多...
课程设计---哈夫曼树的编码与解码（Java详解）

课程设计---哈夫曼树的编码与解码（Java详解）

目录 一.设计任务&&要求&#xff1a; 二.方案设计报告&#xff1a; 2.1 哈夫曼树编码&译码的设计原理&#xff1a; 2.3设计目的&#xff1a; 2.3设计的主要过程&#xff1a; 2.4程序方法清单&#xff1a; 三.整体实现源码&#xff1a; 四.运行结果展示&…
阅读更多...
昇思25天学习打卡营第1天|基本介绍及快速入门

昇思25天学习打卡营第1天|基本介绍及快速入门

1.第一天学习总体复盘 1&#xff09;成功注册昇思大模型平台&#xff0c;并成功申请算力&#xff1b; 2)在jupyter环境下学习初学入门/初学教程的内容&#xff1b; 在基本介绍部分&#xff0c;快速撸了一边内容&#xff0c;有了一个基本的了解&#xff08;没理解到位的计划采用…
阅读更多...
Part 6.2.3 欧拉函数

Part 6.2.3 欧拉函数

欧拉函数φ(x) 表示了小于x的数字中&#xff0c;与x互质的数字个数。 关于欧拉函数的基本知识>欧拉函数的求解< [SDOI2008] 仪仗队 题目描述 作为体育委员&#xff0c;C 君负责这次运动会仪仗队的训练。仪仗队是由学生组成的 N N N \times N NN 的方阵&#xff0c;…
阅读更多...
在VScode中创建PHP环境

在VScode中创建PHP环境

一、下载PHP Server 和 PHP Debug这两个扩展 二、下载完成之后&#xff0c;在VScode中&#xff0c;打开我们写代码的文件 这里是我事先创建好的一些文件&#xff0c;本次环境搭建只需要创建一个.php后缀的文件即可。 先选中.php文件&#xff0c;再点击文件。 点击首选项&#x…
阅读更多...
配置CentOS 7通过MSTSC连接远程桌面

配置CentOS 7通过MSTSC连接远程桌面

正文共&#xff1a;777 字 14 图&#xff0c;预估阅读时间&#xff1a;1 分钟 前面我们介绍了如何通过VNC连接Ubuntu的远程桌面&#xff08;Ubuntu 18.04开启远程桌面连接&#xff09;&#xff0c;也介绍了如何使用微软的MSTSC来连接Ubuntu的远程桌面&#xff08;如何通过MSTSC…
阅读更多...
Flink 1.19.1 standalone 集群模式部署及配置

Flink 1.19.1 standalone 集群模式部署及配置

flink 1.19起 conf/flink-conf.yaml 更改为新的 conf/config.yaml standalone集群: dev001、dev002、dev003 config.yaml: jobmanager address 统一使用 dev001&#xff0c;bind-port 统一改成 0.0.0.0&#xff0c;taskmanager address 分别更改为dev所在host dev001 config.…
阅读更多...
Vue63-配置代理-方式二

Vue63-配置代理-方式二

一、请求前缀&#xff1a;能灵活的控制走不走代理 1-1、请求前缀 有请求前缀的走代理服务器&#xff1b; 没有请求前缀的不走代理服务器。 修改代码中的请求地址&#xff0c;加上请求前缀 报错的原因&#xff1a; 解决方式&#xff1a; 1-2、ws配置项、changeOrigin配置项 二…
阅读更多...
智能合约新项目 链上智能合约前端H5源码 智能合约区块链 以太坊前端调用智能合约

智能合约新项目 链上智能合约前端H5源码 智能合约区块链 以太坊前端调用智能合约

智能合约新项目 链上智能合约前端H5源码 智能合约区块链 以太坊前端调用智能合约 源码下载&#xff1a;https://download.csdn.net/download/m0_66047725/89402192 更多资源下载&#xff1a;关注我。
阅读更多...
Mendix 创客访谈录｜医疗设备领域的数字化转型利器

Mendix 创客访谈录｜医疗设备领域的数字化转型利器

本期创客 尚衍亮 爱德亚&#xff08;北京&#xff09;医疗科技有限公司 应用开发和数字化事业部开发经理 大家好&#xff0c;我叫尚衍亮。毕业于软件工程专业&#xff0c;有6年的软件开发经验。从2021年开始&#xff0c;我在爱德亚&#xff08;北京&#xff09;医疗科技有限公司…
阅读更多...
StarkNet System Architecture 系统架构

StarkNet System Architecture 系统架构

文章目录 Starknet架构排序器，证明器和节点、验证者、Starnet Core排序器 Sequencer证明器 Prover节点验证者StarkNet Core工作原理TransactionsStarknet架构 原文链接： https://david-barreto.com/starknets-architecture-review/#more-4602 StarkNet 有五个组成部分。分别…
阅读更多...
新手装修 避坑课2.0：装修之前一定要做好功课(55节课)

新手装修 避坑课2.0：装修之前一定要做好功课(55节课)

课程下载&#xff1a;https://download.csdn.net/download/m0_66047725/89388333 更多资源下载&#xff1a;关注我。 课程目录 第01节1.装修前准备工作.mp4 第02节开篇.mp4 第03节2.装修需要提前定好的设备和材料.mp4 第04节3.自装还是找装修公司.mp4 第05节4.自装怎么找…
阅读更多...
客观评价，可道云teamOS搭建的企业网盘，如Windows本地电脑一般的使用体验真的蛮不错

客观评价，可道云teamOS搭建的企业网盘，如Windows本地电脑一般的使用体验真的蛮不错

不管是企业网盘还是私有网盘&#xff0c;简单易用一直是我比较在意的。快速能上手使用&#xff0c;甚至不需要习惯一套新的操作逻辑&#xff0c;代表着不需要学习适应&#xff0c;能够迅速投入正常使用。 在这个过程中&#xff0c;可道云teamos以其Windows电脑般的流畅体验&am…
阅读更多...
Ubuntu网络管理命令：nslookup

Ubuntu网络管理命令：nslookup

安装Ubuntu桌面系统&#xff08;虚拟机&#xff09;_虚拟机安装ubuntu桌面版-CSDN博客 nslookup命令主要用来查询域名信息&#xff0c;实际上主要是将域名转换为相应的IP地址&#xff0c;或者将IP地址转换成相应的域名。nslookup命令为用户提供了两种工作模式&#xff0c;分别…
阅读更多...
无引擎游戏开发（2)：最简游戏框架 | EasyX制作井字棋小游戏I

无引擎游戏开发（2)：最简游戏框架 | EasyX制作井字棋小游戏I

一、EasyX中的坐标系 不同于数理中的坐标系&#xff0c;EasyX中的y轴是竖直向下的 二、渲染缓冲区 之前的程序添加了这三个函数改善了绘图时闪烁的情况: 小球在"画布“上移动的过程就是我们在调用绘图函数&#xff0c;这个”画布“就是渲染缓冲区&#xff0c;先绘制的内…
阅读更多...
2024人工智能指数报告（二）：技术性能

2024人工智能指数报告（二）：技术性能

背景 从2017年开始&#xff0c;斯坦福大学人工智能研究所&#xff08;HAI&#xff09;每年都会发布一份人工智能的研究报告&#xff0c;人工智能指数报告&#xff08;AII&#xff09;&#xff0c;对上一年人工智能相关的数据进行跟踪、整理、提炼并进行可视化。这份指数报告被认…
阅读更多...
Java宝藏实验资源库（2）字节流

Java宝藏实验资源库（2）字节流

一、实验目的 掌握输入输出流的基本概念。掌握字节流处理类的基本结构。掌握使用字节流进行输入输出的基本方法。 二、实验内容、过程及结果 *17.10 (Split files) Suppose you want to back up a huge file (e.g., a 10-GB AVI file) to a CD-R. You can achieve it by split…
阅读更多...
前端技术栈三(vue+Axios)

前端技术栈三(vue+Axios)

一、Vue 1 基本介绍 1.1 Vue 是什么? Vue (读音 /vjuː/&#xff0c;类似于 view) 是一个前端框架, 易于构建用户界面 Vue 的核心库只关注视图层&#xff0c;不仅易于上手&#xff0c;还便于与第三方库或项目整合 支持和其它类库结合使用 开发复杂的单页应用非常方便 Vue 是…
阅读更多...
Python的三种方式显示图片

Python的三种方式显示图片

from PIL import Image import numpy as np im Image.open("img.png") #方法一&#xff1a;使用PIL库显示图片 a np.array(im) imImage.fromarray(a) im.show() import matplotlib.pyplot as plt #方法二&#xff1a;使用matplotlib库显示图片 plt.imshow(a) plt.s…
阅读更多...
java 不可变集合的创建和Stream流的使用

java 不可变集合的创建和Stream流的使用

文章目录 一、创建不可变的集合1.1为什么创建不可变的集合1.2 创建List、Set和Map的不可变集合1.2.1 创建List的不可变集合1.2.2 创建Set 的不可变集合1.2.3 创建Map的不可变集合 二、使用集合 的Stream 流2.1 Stream的使用步骤2.2 Stream的方法 三、如何获取Stream 流对象四、…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023