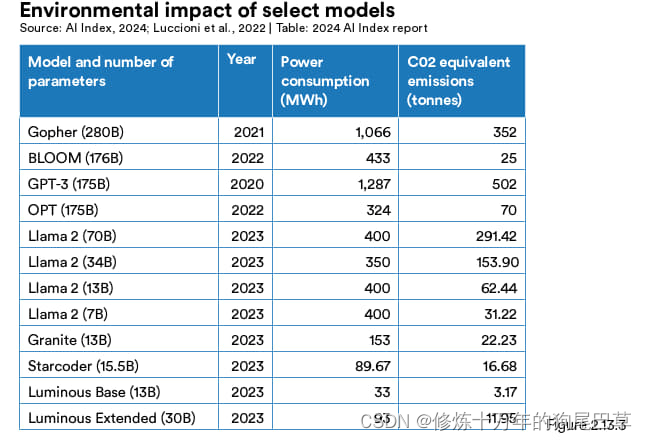
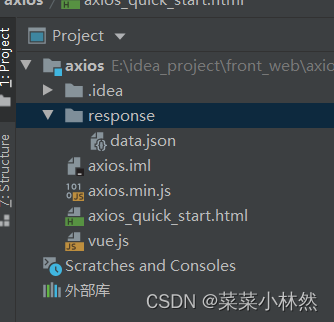
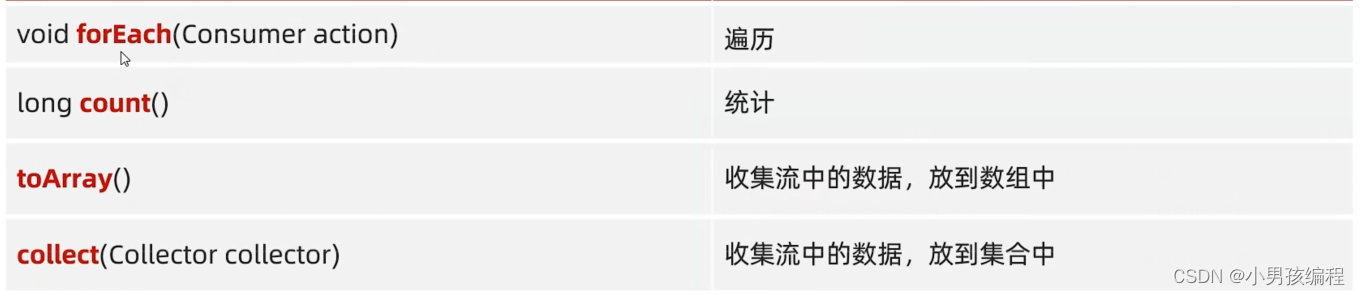
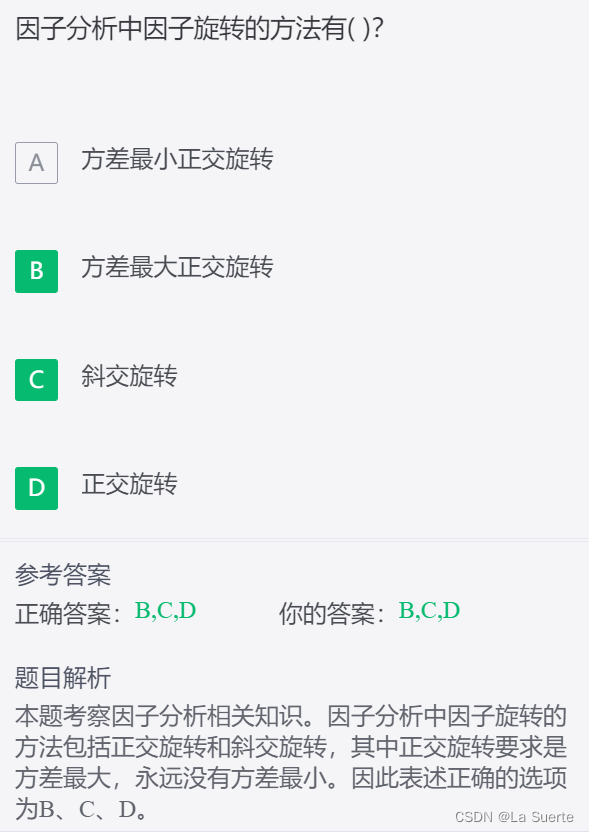
欧拉函数φ(x) 表示了小于x的数字中，与x互质的数字个数。
关于欧拉函数的基本知识>欧拉函数的求解<

[SDOI2008] 仪仗队

题目描述

作为体育委员，C 君负责这次运动会仪仗队的训练。仪仗队是由学生组成的 $N\times N$ 的方阵，为了保证队伍在行进中整齐划一，C 君会跟在仪仗队的左后方，根据其视线所及的学生人数来判断队伍是否整齐（如下图）。

现在，C 君希望你告诉他队伍整齐时能看到的学生人数。

输入格式

一行，一个正整数 $N$。

输出格式

输出一行一个数，即 C 君应看到的学生人数。

样例 #1

样例输入 #1

4

样例输出 #1

9

提示

对于 $100\%$ 的数据，$1\le N\le 40000$。

解题思路

分析问题可知，设一个点到C君的横向和纵向距离分别为m，n,没有被遮挡的充分条件是m，n互质。如何理解？如何m,n不互质，设
gcd（m，n）=p，则一定存在（m/p+1，n/p+1）在队伍中遮挡了该点。而如果m，n互质，则无法找到这个位置。

code

#include<iostream>
using namespace std;
#define MAX_N 40000
int n;
int vis[MAX_N+5];
int phi[MAX_N+5];
int prim[MAX_N+5];
int cnt=0;
void get_phi()
{
	phi[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!vis[i])
		{
			vis[i]=1;
			prim[++cnt]=i;
			phi[i]=i-1;
		}
		for(int j=1;prim[j]*i<=n;j++)
		{
			int m=prim[j]*i;
			vis[m]=1;
			if(i%prim[j]==0)
			{
				phi[m]=prim[j]*phi[i];
				break;
			}
			else{
				phi[m]=(prim[j]-1)*phi[i];
			}
		}
	}
	
	return ;
}
int main()
{
	cin>>n;
	if(n==1)
	{
		cout<<0;
		return 0;
	}
	get_phi();
	long long sum=0;
	for(int i=2;i<=n-1;i++)
	sum+=phi[i];
	long long ans=sum*2+3;
	cout<<ans;
	return 0;
 } 

GCD

题目描述

给定正整数 $n$，求 $1\le x,y\le n$ 且 $\gcd (x,y)$ 为素数的数对 $(x,y)$ 有多少对。

输入格式

只有一行一个整数，代表$n$。

输出格式

一行一个整数表示答案。

样例 #1

样例输入 #1

4

样例输出 #1

4

提示

样例输入输出 1 解释

对于样例，满足条件的 $(x,y)$ 为 $(2,2)$，$(2,4)$，$(3,3)$，$(4,2)$。

---

数据规模与约定

• 对于 $100\%$ 的数据，保证 $1\le n\le 10^7$。

---

来源：bzoj2818。

本题数据为洛谷自造数据，使用 CYaRon 耗时 $5$ 分钟完成数据制作。

解题思路

如果gcd(a,b)=1，则gcd(a *p,b *p)=p。若p为质数且p<n/b，则a *p和b *p是符合题意的一组解。
求出所有数的欧拉函数以及小于n/p的质数的数量，根据其乘积便可以求出答案。

code

#include<iostream>
using namespace std;
#define MAX_N 10000000
int vis[MAX_N+5];
int prim[MAX_N+5];
int phi[MAX_N+5];
int cnt_prim[MAX_N+5];
int cnt=0;
int n;
void get_phi()
{
	phi[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!vis[i])
		{
			vis[i]=1;
			prim[++cnt]=i;
			phi[i]=i-1;
		}
		for(int j=1;prim[j]*i<=n;j++)
		{
			int m=prim[j]*i;
			vis[m]=1;
			if(i%prim[j]==0)
			{
				phi[m]=prim[j]*phi[i];
				break;
			}
			else{
				phi[m]=(prim[j]-1)*phi[i];
			}
		}
	}
	return ;
}
int main()
{
	cin>>n;
	get_phi();
	int st=0,ed=n;
	for(int i=cnt;i>=1;i--)
	{
		st=prim[i];
		for(int j=st;j<=ed;j++)
		cnt_prim[j]=i;
		ed=prim[i]-1;
	}
	long long ans=0;
	for(int i=2;i<=n;i++)
	{
		ans+=cnt_prim[n/i]*phi[i]*2;
	}
	ans+=cnt_prim[n];
	cout<<ans;
	return 0;
}

GCD SUM

题目描述

求

$$\sum _{i=1}^n\sum _{j=1}^n\gcd (i,j)$$

输入格式

第一行一个整数 $n$。

输出格式

第一行一个整数表示答案。

样例 #1

样例输入 #1

2

样例输出 #1

5

提示

对于 $30\%$ 的数据，$n\le 3000$。

对于 $60\%$ 的数据，$7000\le n\le 7100$。

对于 $100\%$ 的数据，$n\le 10^5$。

解题思路

答题思路类似于上题。
如果gcd(a,b)=1，则gcd(a *p,b *p)=p。若p<n/b,则a *p和b *p是符合题意的一组解。
对于每一组数，无非就是gcd(a,b)=1和大于1两种情况，等于1也即互质，其数量是包括在欧拉函数中的，大于1则是根据a,b同时 *p转化而来的，易求。
和上题的区别在于，上一题维护cnt_prim数组，本题维护区间和数组sum。

code

#include<iostream>
using namespace std;
#define MAX_N 100000
int vis[MAX_N+5];
int prim[MAX_N+5];
int phi[MAX_N+5];
long long sum[MAX_N+5];
int cnt=0;
int n;
void get_phi()
{
	phi[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!vis[i])
		{
			vis[i]=1;
			prim[++cnt]=i;
			phi[i]=i-1;
		}
		for(int j=1;prim[j]*i<=n;j++)
		{
			int m=prim[j]*i;
			vis[m]=1;
			if(i%prim[j]==0)
			{
				phi[m]=prim[j]*phi[i];
				break;
			}
			else{
				phi[m]=(prim[j]-1)*phi[i];
			}
		}
	}
	return ;
}
int main()
{
	cin>>n;
	get_phi();
	for(int i=1;i<=n;i++)
	{
		sum[i]=i;
		sum[i]+=sum[i-1];
	}
	long long ans=0;
	for(int i=2;i<=n;i++)
	{
		ans+=phi[i]*sum[n/i]*2;
	}
	ans+=sum[n];
	cout<<ans;
	return 0;
}