ACIS采用自底向上的方式创建box

news2024/7/30 2:12:34

在学习任何CAD几何内核的时候，首先需要学习的是这个几何内核的几何拓扑数据结构，学习完毕后，一个很好的练习是自己采用底层的几何、拓扑构建API，创建一个box。通过这个练习，可以加深初学者对所学几何内核数据结构的理解和认识。

https://www.cnblogs.com/opencascade/p/4102570.html这篇博客介绍了在Open cascade中，采用自底向上的方式如何构建box，本文以ACIS为例，介绍ACIS中，如何采用自底向上的方式创建box。

构建需要的注意事项如下：

1. 首先需要构造出了四面体几何元素，4个Apoint，6个Straight类型的Curve，以及4个Pane类型的Surface；

2. 然后构造出vertex、edge、coedge、loop、face、shell、lump、body这些拓扑，设置vertex、edge、coedge、face指钎指向对应的几何，再把拓扑关系的指针设置好；

3.还要注意curve与edge之间，edge与coedge之间，coedge与edge之间，face与surface之间的方同关系。

代码如下：

BODY* block(SPAposition& min, SPAposition& max)
{
	BODY* body = NULL;

	// initialize bulletin board
	API_BEGIN //初始化了异常处理和事务管理环境
		//设置异常检查机制，确保在建模操作中捕获和处理异常，防止程序崩溃

		// ***********************
		//  CREATE THE GEOMETRY.
		// ***********************

		// create 8 points
	APOINT* p0 = new APOINT(min.x(), min.y(), min.z());
	APOINT* p1 = new APOINT(max.x(), min.y(), min.z());
	APOINT* p2 = new APOINT(min.x(), max.y(), min.z());
	APOINT* p3 = new APOINT(max.x(), max.y(), min.z());

	APOINT* p4 = new APOINT(min.x(), min.y(), max.z());
	APOINT* p5 = new APOINT(max.x(), min.y(), max.z());
	APOINT* p6 = new APOINT(min.x(), max.y(), max.z());
	APOINT* p7 = new APOINT(max.x(), max.y(), max.z());

	// create 12 straight lines
	//为了简化边的构建，我们选择了直线的方向与图示中的边方向一致
	STRAIGHT* s0 = new STRAIGHT(p0->coords(), SPAunit_vector(1.0, 0.0, 0.0));
	STRAIGHT* s1 = new STRAIGHT(p1->coords(), SPAunit_vector(0.0, 1.0, 0.0));
	STRAIGHT* s2 = new STRAIGHT(p3->coords(), SPAunit_vector(-1.0, 0.0, 0.0));
	STRAIGHT* s3 = new STRAIGHT(p2->coords(), SPAunit_vector(0.0, -1.0, 0.0));

	STRAIGHT* s4 = new STRAIGHT(p4->coords(), SPAunit_vector(1.0, 0.0, 0.0));
	STRAIGHT* s5 = new STRAIGHT(p5->coords(), SPAunit_vector(0.0, 1.0, 0.0));
	STRAIGHT* s6 = new STRAIGHT(p7->coords(), SPAunit_vector(-1.0, 0.0, 0.0));
	STRAIGHT* s7 = new STRAIGHT(p6->coords(), SPAunit_vector(0.0, -1.0, 0.0));

	STRAIGHT* s8 = new STRAIGHT(p0->coords(), SPAunit_vector(0.0, 0.0, 1.0));
	STRAIGHT* s9 = new STRAIGHT(p1->coords(), SPAunit_vector(0.0, 0.0, 1.0));
	STRAIGHT* s10 = new STRAIGHT(p3->coords(), SPAunit_vector(0.0, 0.0, 1.0));
	STRAIGHT* s11 = new STRAIGHT(p2->coords(), SPAunit_vector(0.0, 0.0, 1.0));

	// create 6 planar surfaces
	//所有的平面的法线方向都被定义为指向体的外部，这将简化后续面定义的过程
	PLANE* pln0 = new PLANE(p0->coords(), SPAunit_vector(0.0, 0.0, -1.0));
	PLANE* pln1 = new PLANE(p4->coords(), SPAunit_vector(0.0, 0.0, 1.0));
	PLANE* pln2 = new PLANE(p0->coords(), SPAunit_vector(0.0, -1.0, 0.0));
	PLANE* pln3 = new PLANE(p1->coords(), SPAunit_vector(1.0, 0.0, 0.0));
	PLANE* pln4 = new PLANE(p3->coords(), SPAunit_vector(0.0, 1.0, 0.0));
	PLANE* pln5 = new PLANE(p2->coords(), SPAunit_vector(-1.0, 0.0, 0.0));

	// ***********************
	//  CREATE THE TOPOLOGY.
	// ***********************

	// create 8 verticies
	VERTEX* v0 = new VERTEX(p0);
	VERTEX* v1 = new VERTEX(p1);
	VERTEX* v2 = new VERTEX(p2);
	VERTEX* v3 = new VERTEX(p3);
	VERTEX* v4 = new VERTEX(p4);
	VERTEX* v5 = new VERTEX(p5);
	VERTEX* v6 = new VERTEX(p6);
	VERTEX* v7 = new VERTEX(p7);

	// create 12 edges
	//EDGE类的构造函数需要起始顶点、结束顶点、曲线（CURVE）以及边相对于曲线的方向
	EDGE* e0 = new EDGE(v0, v1, s0, FORWARD);
	EDGE* e1 = new EDGE(v1, v3, s1, FORWARD);
	EDGE* e2 = new EDGE(v3, v2, s2, FORWARD);
	EDGE* e3 = new EDGE(v2, v0, s3, FORWARD);

	EDGE* e4 = new EDGE(v4, v5, s4, FORWARD);
	EDGE* e5 = new EDGE(v5, v7, s5, FORWARD);
	EDGE* e6 = new EDGE(v7, v6, s6, FORWARD);
	EDGE* e7 = new EDGE(v6, v4, s7, FORWARD);

	EDGE* e8 = new EDGE(v0, v4, s8, FORWARD);
	EDGE* e9 = new EDGE(v1, v5, s9, FORWARD);
	EDGE* e10 = new EDGE(v3, v7, s10, FORWARD);
	EDGE* e11 = new EDGE(v2, v6, s11, FORWARD);

	// create loops of coedges
	// loop of coedges on the low-z plane
	//COEDGE类的构造函数需要一个EDGE、coedge相对于边的方向、前一个coedge和下一个coedge。
	//（coedge环形成一个双向链表，每个coedge中都有前一个和下一个指针。）
	COEDGE* c0 = new COEDGE(e0, REVERSED, NULL, NULL);
	COEDGE* c3 = new COEDGE(e3, REVERSED, c0, NULL);
	COEDGE* c2 = new COEDGE(e2, REVERSED, c3, NULL);
	COEDGE* c1 = new COEDGE(e1, REVERSED, c2, c0);
	LOOP* l0 = new LOOP(c0, NULL);

	// loop of coedges on the high-z plane
	COEDGE* c4 = new COEDGE(e4, FORWARD, NULL, NULL);
	COEDGE* c5 = new COEDGE(e5, FORWARD, c4, NULL);
	COEDGE* c6 = new COEDGE(e6, FORWARD, c5, NULL);
	COEDGE* c7 = new COEDGE(e7, FORWARD, c6, c4);
	LOOP* l1 = new LOOP(c4, NULL);

	// loop of coedges on the low-y plane
	c0 = new COEDGE(e0, FORWARD, NULL, NULL);
	COEDGE* c9 = new COEDGE(e9, FORWARD, c0, NULL);
	c4 = new COEDGE(e4, REVERSED, c9, NULL);
	COEDGE* c8 = new COEDGE(e8, REVERSED, c4, c0);
	LOOP* l2 = new LOOP(c0, NULL);

	// loop of coedges on the high-x plane
	c1 = new COEDGE(e1, FORWARD, NULL, NULL);
	COEDGE* c10 = new COEDGE(e10, FORWARD, c1, NULL);
	c5 = new COEDGE(e5, REVERSED, c10, NULL);
	c9 = new COEDGE(e9, REVERSED, c5, c1);
	LOOP* l3 = new LOOP(c1, NULL);

	// loop of coedges on the high-y plane
	c2 = new COEDGE(e2, FORWARD, NULL, NULL);
	COEDGE* c11 = new COEDGE(e11, FORWARD, c2, NULL);
	c6 = new COEDGE(e6, REVERSED, c11, NULL);
	c10 = new COEDGE(e10, REVERSED, c6, c2);
	LOOP* l4 = new LOOP(c2, NULL);

	// loop of coedges on the low-x plane
	c3 = new COEDGE(e3, FORWARD, NULL, NULL);
	c8 = new COEDGE(e8, FORWARD, c3, NULL);
	c7 = new COEDGE(e7, REVERSED, c8, NULL);
	c11 = new COEDGE(e11, REVERSED, c7, c3);
	LOOP* l5 = new LOOP(c3, NULL);

	// create 6 faces
	//FACE类的构造函数需要一个指向环的指针、一个指向下一个面的指针、
	//	一个指向基础表面的指针以及面相对于表面的方向。
	FACE* f0 = new FACE(l0, NULL, pln0, FORWARD);
	FACE* f1 = new FACE(l1, f0, pln1, FORWARD);
	FACE* f2 = new FACE(l2, f1, pln2, FORWARD);
	FACE* f3 = new FACE(l3, f2, pln3, FORWARD);
	FACE* f4 = new FACE(l4, f3, pln4, FORWARD);
	FACE* f5 = new FACE(l5, f4, pln5, FORWARD);

	// create 1 shell, 1 lump, and 1 body
	//SHELL类的构造函数需要一个指向面链表中第一个面的指针f5，
	//一个指向子壳列表的指针，以及一个指向块中下一个壳的指针
	body = new BODY(new LUMP(new SHELL(f5, NULL, NULL), NULL));

	// terminate bulletin board
	API_END

		return body;
}

通过与Open cascade的构建过程对比，有如下主要不同：

1. OCC创建Edge时，创建接口只需要传入几何Geom_Line，然后再把顶点Vertex关联上，ACIS的接口就比较完善，EDGE类的构造函数需要起始顶点、结束顶点、曲线（CURVE）以及边相对于曲线的方向；

2. OCC创建Wire或者Shell的时候，需要手动一个一个添加对应的Edge和Face，但是ACIS不需要，ACIS中EDGE、COEDGE、FACE都在一个链表中，只需要把链表头传递进去就可以了；

3. OCC创建的时候，PCurve需要手动创建并添加，但是ACIS中，默认在new FACE的时候，就把对应的PCurve创建好了，不需要人工创建了。

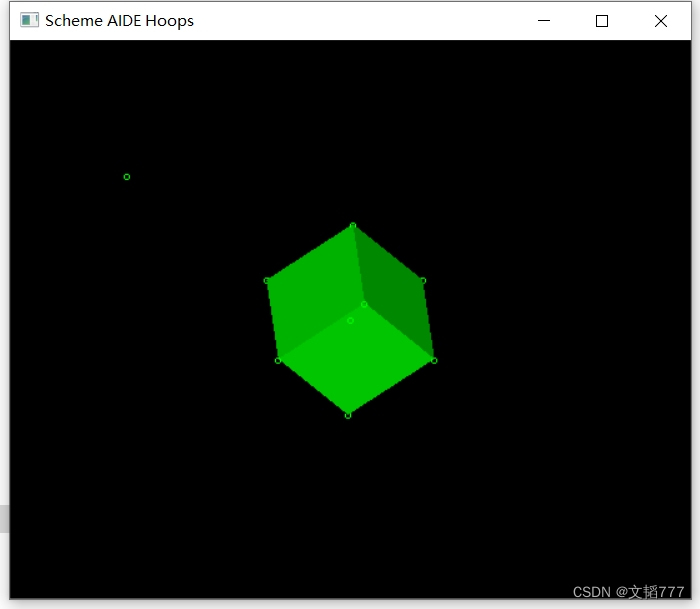
最终结果如图：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1840718.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

AXI三板斧之Outstanding、Out-of-order、interleaving

AXI三板斧之Outstanding、Out-of-order、interleaving

1、AXI三板斧之Outstanding 可以不用等单个命令的响应，直接连续发送N个命令（N>1），假设Slave端的Outstanding能力为N时（N>1），那么Master端可以在Slave不返回读数据的情况下，连…
阅读更多...
从小白到大神：算法工程师的核心竞争力养成计划！

从小白到大神：算法工程师的核心竞争力养成计划！

从小白到大神：算法工程师的核心竞争力养成计划！ 我们会发现，本科及研究生所学的知识，比如高等数学、线性代数、传统机器学习方法及深度学习理论等这些，都只是作为算法学习的基础，并不能成为算法工程师的核…
阅读更多...
React@16.x（34）动画（中）

React@16.x（34）动画（中）

目录 3，SwitchTransition3.1，原理3.1.2，key3.1.2，mode 3.2，举例3.3，结合 animate.css 4，TransitionGroup4.1，其他属性4.1.2，appear4.1.2，component4.1.3&…
阅读更多...
【Python】对应接口url 被编码后的处理

【Python】对应接口url 被编码后的处理

Python 系列 文章目录 Python 系列前言一、网页链接是什么？二、使用步骤1.解码 总结 前言 提示：这里可以添加本文要记录的大概内容： 我们在查找网页的开发代码的时候，可能经常查看到接口的链接是： %7B%22funName%22%…
阅读更多...
昇思25天学习打卡营第1天|快速入门

昇思25天学习打卡营第1天|快速入门

一、简介： 本节通过MindSpore已经封装好的API，快速实现一个深度学习模型的数据集准备、训练评估，模型参数保存和加载，对新手朋友十分友好。这里非常感谢华为昇思团队在算力和代码方面的指导。 二、环境准备： 在开始…
阅读更多...
YOLOv10改进 | Conv篇 |YOLOv10引入DBB卷积（助力涨点）

YOLOv10改进 | Conv篇 |YOLOv10引入DBB卷积（助力涨点）

1. DBB介绍 1.1 摘要：我们提出了卷积神经网络（ConvNet）的通用构建块来提高性能，而无需任何推理时间成本。 该块被称为多样化分支块（DBB），它通过组合不同尺度和复杂度的不同分支来丰富特征空间，从而增强单个卷积的表示能力，包括卷积序列、多尺度卷积和平均池化。 训练后…
阅读更多...
参花实业增收不增利：曾被执行近3000万，资产负债比率高达166%

参花实业增收不增利：曾被执行近3000万，资产负债比率高达166%

《港湾商业观察》廖紫雯 日前，参花实业控股有限公司（以下简称：参花实业）再度递表港交所，保荐机构为中泰国际，参花实业国内运营主体为固安县参花面粉有限公司、廊坊固安县参花企业管理有限公司。 作为一家…
阅读更多...
【linux】Valgrind工具集详解（十六）：交叉编译、移植到arm（失败）

【linux】Valgrind工具集详解（十六）：交叉编译、移植到arm（失败）

1、源码下载 官网：https://valgrind.org/ 源码：https://valgrind.org/downloads/current.html 2、配置 ./configure CC=arm-linux-gnueabihf-gcc \CXX=arm-linux-gnueabihf-g++ \AR=arm-linux-gnueabihf-ar \--host=arm-linux-gnueabihf \--pr
阅读更多...
Mkdocs中文系列教程补充（1）

Mkdocs中文系列教程补充（1）

什么是requirements.txt 我的理解是mkdocs依赖的py库 第一次建立MKdocs文档使用 mkdocs new . 完后，比较建议执行一下： pip install -r requirements.txt 不然mkdocs serve后会出现什么 xxx not found ，比如下面这位老哥 示例 mkdocs …
阅读更多...
CleanShot X for Mac v4.7 屏幕截图录像工具（保姆级教程，小白轻松上手，简单易学）

CleanShot X for Mac v4.7 屏幕截图录像工具（保姆级教程，小白轻松上手，简单易学）

Mac分享吧 文章目录 一、准备工作二、部分特有功能效果1、截图软件的普遍常用功能（画框、箭头、加文字等）都具备，不再详细介绍2、ABCD、1234等信息标注（每按一下鼠标，即各是A、B、C、D...等）3、截图更换背…
阅读更多...
MySQL日志（三）：数据安全

MySQL日志（三）：数据安全

先来看一个结论：只要redo log和binlog保证持久化到磁盘， 就能确保MySQL异常重启后， 数据可以恢复。 binlog写入逻辑 binlog的写入逻辑比较简单： 事务执行过程中， 先把日志写到binlog cache， 事务提交的时候…
阅读更多...
【论文阅读】-- MIRIA：用于时空交互数据原位可视化和分析的混合现实工具包

【论文阅读】-- MIRIA：用于时空交互数据原位可视化和分析的混合现实工具包

MIRIA: A Mixed Reality Toolkit for the In-Situ Visualization and Analysis of Spatio-Temporal Interaction Data 摘要1 引言2 背景及相关工作2.1 用户交互和运动数据分析2.2 沉浸式分析 3 时空用户交互分析3.1 现有系统的用例和分析3.2 要求 4 MIRIA 工具包4.1 一般概念4.…
阅读更多...
基于matlab的RRT算法路径规划（附带案例源码）

基于matlab的RRT算法路径规划（附带案例源码）

文章中的所有案例均为博主手动复现，用于记录博主学习路径规划的过程，如有不妥，欢迎在评论区交流 目录 1 标准RRT1.1 算法原理1.2 演示 2 GBRRT2.1 算法原理2.2 算法演示 3 RRT-STAR3.1 算法原理3.2 算法演示 4 RRT-CONNECT4.1 算法原理4.2 算…
阅读更多...
[NewStarCTF 2023 公开赛道]R!C!E!

[NewStarCTF 2023 公开赛道]R!C!E!

好久没写了。今天儿弄一个rce 题很直接&#xff0c;好久没这么直白的题了&#xff0c;看源码 <?php highlight_file(__FILE__); if(isset($_POST[password])&&isset($_POST[e_v.a.l])){$passwordmd5($_POST[password]);$code$_POST[e_v.a.l];if(substr($password…
阅读更多...
css怎么绘制一个三角形

css怎么绘制一个三角形

说在前面 在CSS中画三角形通常利用border属性来实现&#xff0c;通过设置三个边的宽度为0&#xff0c;并为一个边提供颜色&#xff0c;结合transform属性进行旋转&#xff0c;可以创建一个三角形。以下是几种常见的CSS三角形的实现方法&#xff1a; 方法1&#xff1a;使用borde…
阅读更多...
EXCELITAS电源维修TLX302高压电源维修

EXCELITAS电源维修TLX302高压电源维修

埃赛力达电源维修 EXCELITAS电源维修 海曼电源维修 高压电源维修 EXCELITAS高压电源维修故障包括&#xff1a;无输出&#xff0c;高压达不到&#xff0c;电流达不到标准&#xff0c;高压打火,高压线接头处太靠近铁壳部分。无光,风扇不转。保险丝断&#xff0c;可以强制发光,不…
阅读更多...
RadioML 2016.10a 调制方式识别

RadioML 2016.10a 调制方式识别

RadioML 2016.10a 调制方式识别 MLP、CNN、ResNet X [] lbl [] for mod in mods:for snr in snrs:X.append(Xd[(mod,snr)])for i in range(Xd[(mod,snr)].shape[0]):lbl.append((mod,snr)) X np.vstack(X) file.close()上述论文的分类任务是识别和区分不同类型的无线电调制…
阅读更多...
深度解析ISO9001质量管理体系认证的核心优势

深度解析ISO9001质量管理体系认证的核心优势

ISO9001质量管理体系认证是一项全球通用的标准&#xff0c;旨在帮助企业优化质量管理&#xff0c;提升市场竞争力。本文将详细解析ISO9001认证为企业带来的多重核心优势。 首先&#xff0c;ISO9001认证显著提升了企业的产品和服务质量。通过建立和实施系统化的质量管理流程&…
阅读更多...
一个简单、快速用于训练和微调中等规模GPT模型的开源项目

一个简单、快速用于训练和微调中等规模GPT模型的开源项目

大家好&#xff0c;今天给大家分享的是一个简单、快速用于训练和微调中等规模GPT模型的开源项目&#xff0c;该项目旨在拓宽深度学习领域的应用&#xff0c;特别是为深度学习的入门者提供便利。 Nano GPT是一个基于PyTorch的开源项目&#xff0c;由前特斯拉AI负责人Andrej Ka…
阅读更多...
【Windows】一键设置默认浏览器

【Windows】一键设置默认浏览器

最近&#xff0c;有人向我求助&#xff0c;希望我能帮助他们实现一键设置Chrome为默认浏览器。我心想&#xff0c;这有何难&#xff1f;改个注册表不就搞定了嘛。很多软件不都是这么做的吗&#xff1f;找到对应的注册表项&#xff0c;快速、准确地修改&#xff0c;然后…结果却…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023