文章目录
- 1 多类分类
- 1.1数据集
- 1.2 数据可视化
- 1.3 向量化逻辑回归
- 1.3.1 向量化代价函数
- 1.3.2 矢量化梯度下降以及正则化表达
- 1.4 一对多分类
- 2.神经网络
- 2.1模型表示
- 总结(自己训练求解参数全流程)
1 多类分类
在本练习中,您将使用逻辑回归和神经网络来识别手写数字(从 0 到 9)。如今,自动手写数字识别被广泛使用 - 从识别邮件信封上的邮政编码到识别银行支票上的金额。本练习将向您展示如何将您学到的方法用于此分类任务。在练习的第一部分,您将扩展之前的逻辑回归实现并将其应用于一对多分类。
在练习的第一部分,您将扩展之前的逻辑回归实现并将其应用于一对多分类。
1.1数据集
import numpy as np # 导入NumPy库,用于进行数组和矩阵运算
import pandas as pd # 导入Pandas库,用于数据处理和分析
import matplotlib.pyplot as plt # 导入Matplotlib库中的pyplot模块,用于数据可视化
from scipy.io import loadmat # 从SciPy库中导入loadmat函数,用于读取MATLAB文件
您将获得 ex3data1.mat 中的一个数据集,其中包含 5000 个手写数字的训练示例。
def load_data(path):
data = loadmat(path) # 使用loadmat函数加载MATLAB文件
X = data['X'] # 提取特征数据X
y = data['y'] # 提取标签数据y
return X, y # 返回提取的特征数据和标签数据
ex3data1.mat 中有 5000 个训练示例,其中每个训练示例都是一个 20 像素 x 20 像素的数字灰度图像。每个像素都由一个浮点数表示,表示该位置的灰度强度。20 x 20 的像素网格被“展开”为一个 400 维的向量。这些训练示例中的每一个都成为我们数据矩阵 X 中的一行。这为我们提供了一个 5000 x 400 的矩阵 X,其中每一行都是手写数字图像的训练示例。
X, y = load_data('ex3data1.mat') # 加载MATLAB文件中的数据,并将特征数据赋值给X,标签数据赋值给y
print(np.unique(y)) # 打印标签数据中的唯一值,用于查看有几类标签
# 期望输出:[ 1 2 3 4 5 6 7 8 9 10]
X.shape, y.shape # 获取并输出特征数据和标签数据的形状
# 期望输出:((5000, 400), (5000, 1))
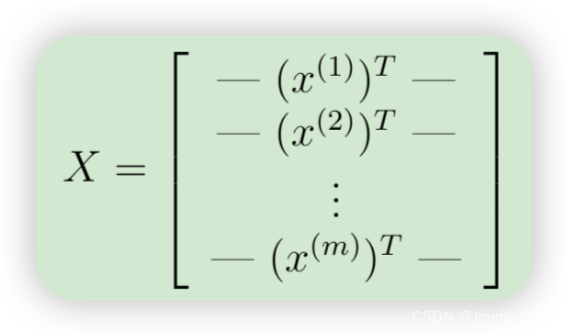
训练集的第二部分是一个 5000 维向量 y,其中包含训练集的标签。为了与 Octave/MATLAB 索引(其中没有零索引)更兼容,我们将数字零映射到值十。因此,“0”数字被标记为“10”,而“1”到“9”的数字按其自然顺序标记为“1”到“9”。
1.2 数据可视化
您将首先可视化训练集的一个子集。在 ex3.m 的第 1 部分中,代码从 X 中随机选择 100 行,并将这些行传递给 displayData 函数。此函数将每行映射到 20 像素 x 20 像素的灰度图像,并将图像一起显示。我们提供了 displayData 函数,鼓励您检查代码以了解其工作原理。运行此步骤后,您应该看到类似图 1 的图像。

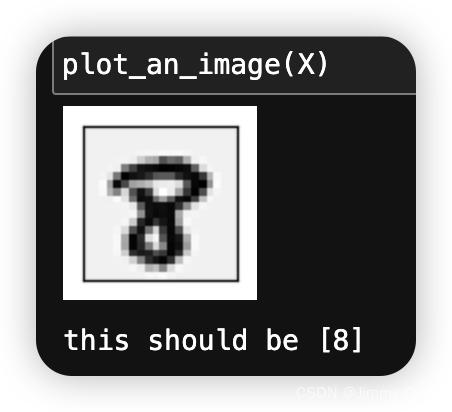
def plot_an_image(X):
"""
随机打印一个数字
"""
pick_one = np.random.randint(0, 5000) # 生成一个0到4999之间的随机整数,作为随机选择的图像索引
image = X[pick_one, :] # 从X中选择随机索引pick_one对应的图像数据
fig, ax = plt.subplots(figsize=(1, 1)) # 创建一个1x1英寸的图形和子图
ax.matshow(image.reshape((20, 20)), cmap='gray_r') # 将图像数据重新调整为20x20,并在子图中显示为反转的灰度图
plt.xticks([]) # 去除x轴刻度,美观
plt.yticks([]) # 去除y轴刻度,美观
plt.show() # 显示图形
print('this should be {}'.format(y[pick_one])) # 打印随机选择的图像对应的标签
1.3 向量化逻辑回归
您将使用多个一对多逻辑回归模型来构建多类分类器。由于有 10 个类别,您需要训练 10 个单独的逻辑回归分类器。为了提高训练效率,确保您的代码经过良好的矢量化非常重要。在本节中,您将实现不使用任何 for 循环的逻辑回归的矢量化版本。您可以使用上一个练习中的代码作为本练习的起点。
1.3.1 向量化代价函数
我们将首先编写成本函数的矢量化版本。回想一下,在(非正则化的)逻辑回归中,成本函数是
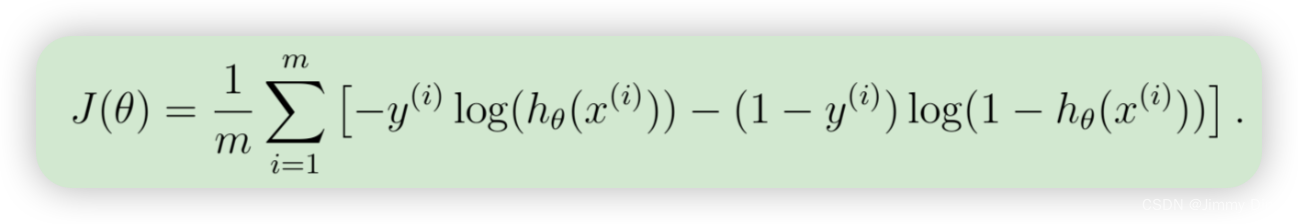
为了计算总和中的每个元素,我们必须计算每个i中的hθ(x(i)),其中
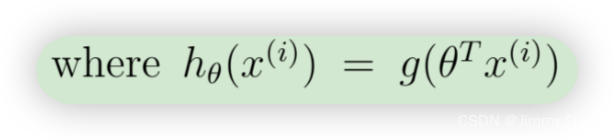
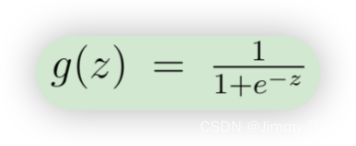
事实证明,我们可以通过使用矩阵乘法快速计算所有示例。让我们将 X 和 θ 定义为
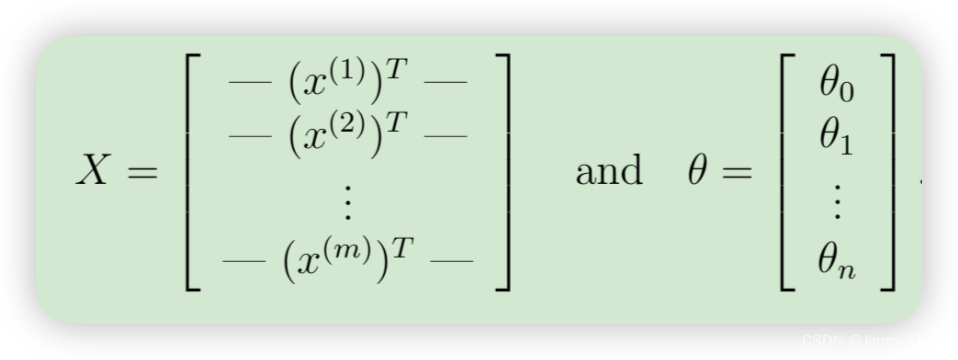
然后,通过计算矩阵乘积 Xθ,我们得到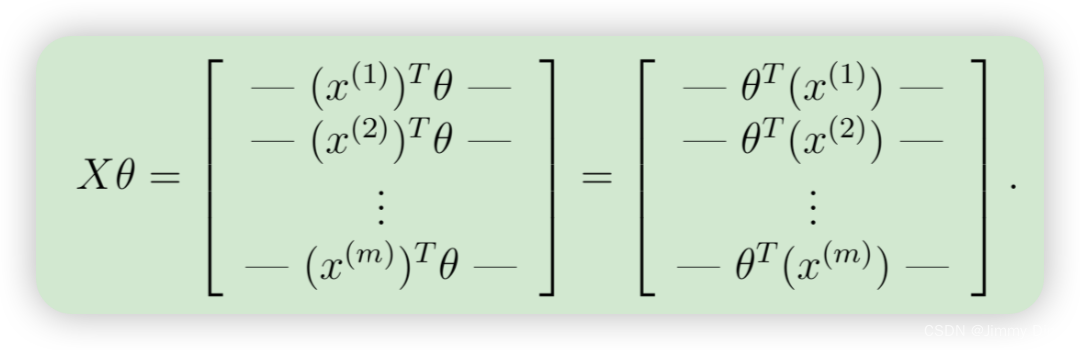
这样,我们只需一行代码就能计算出所有示例 i 的乘积 θX,你的任务是将非正则化成本函数写入文件 lrCostFunction.m,你的实现应该使用我们上面提出的策略来计算θX。您还应该对其余的成本函数使用矢量化方法。 lrCostFunction.m 的完全矢量化版本不应包含任何循环。
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def regularized_cost(theta, X, y, l):
# 提取 theta 的子向量 thetaReg,去除第一个参数 theta_0
thetaReg = theta[1:]
# 计算逻辑回归的交叉熵损失部分,不包括正则化项
first = (-y * np.log(sigmoid(X @ theta))) + (y - 1) * np.log(1 - sigmoid(X @ theta))
# 计算正则化项
reg = (thetaReg @ thetaReg) * l / (2 * len(X))
# 返回总成本,包含交叉熵损失和正则化项
return np.mean(first) + reg
1.3.2 矢量化梯度下降以及正则化表达
回想一下,(非正则化的)逻辑回归成本的梯度是一个向量,其中第 j 个元素定义为
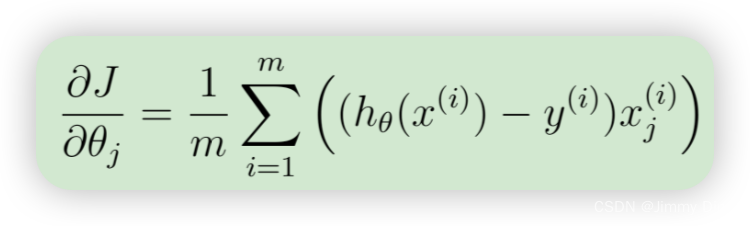
为了在数据集上矢量化此操作,我们首先明确写出所有 θj的偏导数

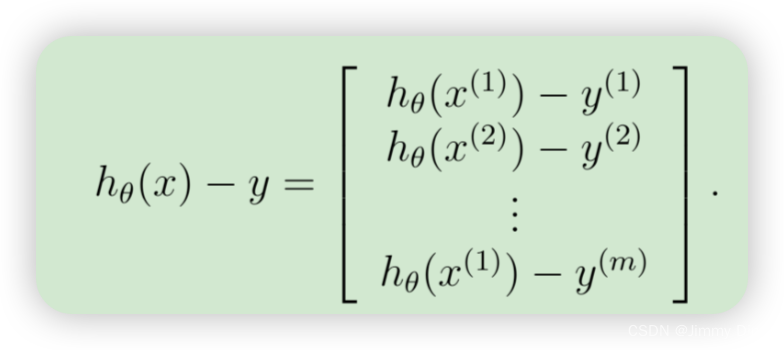
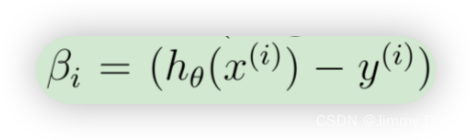
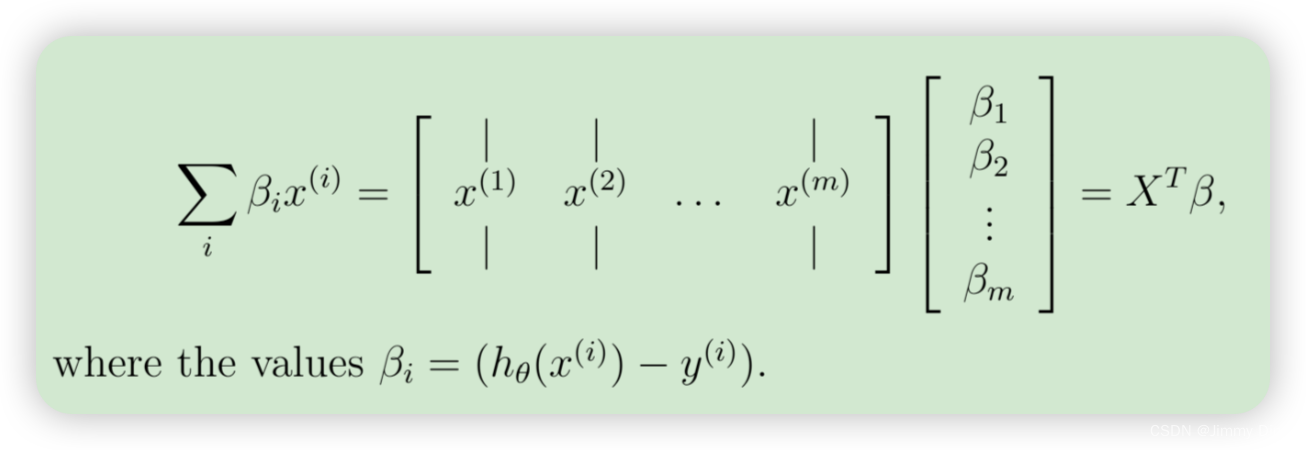
上面的表达式允许我们计算所有偏导数,而无需任何循环。如果您熟悉线性代数,我们鼓励您完成上面的矩阵乘法,以说服自己矢量化版本执行相同的计算。您现在应该实现公式 1 来计算正确的矢量化梯度。完成后,通过实现梯度来完成函数 lrCostFunction.m
def regularized_gradient(theta, X, y, l):
"""
don't penalize theta_0
args:
l: lambda constant
return:
a vector of gradient
"""
# 提取 theta 的子向量 thetaReg,去除第一个参数 theta_0
thetaReg = theta[1:]
# 计算不包含正则化项的梯度
first = (1 / len(X)) * X.T @ (sigmoid(X @ theta) - y)
# 计算正则化项,并插入一维 0 以确保对 theta_0 不进行惩罚
reg = np.concatenate([np.array([0]), (l / len(X)) * thetaReg])
# 返回包含正则化项的总梯度
return first + reg
1.4 一对多分类
在本部分练习中,您将通过训练多个正则化逻辑回归分类器来实现一对多分类,每个分类器对应我们数据集中的 K 个类别(图 1)。在手写数字数据集中,K = 10,但您的代码应该适用于任何 K 值。
现在,您应该完成 oneVsAll.m 中的代码,为每个类别训练一个分类器。具体来说,您的代码应该以矩阵形式返回所有分类器参数Θ,其中 Θ 的每一行对应于一个类的已学习的逻辑回归参数。您可以使用从 1 到 K 的“for”循环来执行此操作,独立训练每个分类器。请注意,此函数的 y 参数是一个从 1 到 10 的标签向量,其中我们将数字“0”映射到标签 10(以避免与索引混淆)。
from scipy.optimize import minimize
import numpy as np
def one_vs_all(X, y, l, K):
"""
使用一对多方法的广义逻辑回归
参数:
X: 特征矩阵,形状为 (m, n+1),其中 m 是样本数量,n+1 是特征数量(包括截距项 x0=1)
y: 目标向量,形状为 (m, ),包含样本的标签
l: 正则化参数 lambda,用于控制正则化强度
K: 类别数量
返回:
all_theta: 形状为 (K, n+1) 的矩阵,包含每个类别训练后的参数
"""
# 初始化参数矩阵 all_theta,用于存储每个类别的训练参数
all_theta = np.zeros((K, X.shape[1])) # 形状为 (K, n+1)
# 遍历每个类别,从1到K(假设类别标签为 1, 2, ..., K)
for i in range(1, K + 1):
# 初始化当前类别的参数向量 theta,初始值为0
theta = np.zeros(X.shape[1])
# 创建当前类别的二元目标向量 y_i
# 如果样本的标签为当前类别 i,则设为1,否则设为0
y_i = np.array([1 if label == i else 0 for label in y])
# 使用 minimize 函数优化正则化成本函数
ret = minimize(fun=regularized_cost, # 目标函数为正则化成本函数
x0=theta, # 初始参数向量 theta
args=(X, y_i, l), # 传递给目标函数的额外参数(X, y_i, l)
method='TNC', # 使用的优化算法为 TNC(信赖区域牛顿共轭梯度法)
jac=regularized_gradient, # 梯度函数
options={'disp': True}) # 显示优化过程的信息
# 将优化后的参数存储到 all_theta 的对应行中
all_theta[i-1, :] = ret.x
# 返回包含所有类别优化参数的矩阵
return all_theta
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def predict_all(X, all_theta):
"""
预测每个样本的类别
参数:
X: 特征矩阵,形状为 (m, n+1),其中 m 是样本数量,n+1 是特征数量(包括截距项 x0=1)
all_theta: 训练好的参数矩阵,形状为 (K, n+1),其中 K 是类别数量
返回:
h_argmax: 预测的类别标签,形状为 (m, )
"""
# 计算每个样本属于每个类别的概率
h = sigmoid(X @ all_theta.T) # 注意这里的 all_theta 需要转置
# 找到每个样本中概率最大的类别的索引
h_argmax = np.argmax(h, axis=1)
# 因为类别是从1开始,而索引是从0开始,所以需要加1
h_argmax = h_argmax + 1
# 返回预测的类别标签
return h_argmax
# 加载所需的库
import numpy as np
from scipy.io import loadmat
# 定义数据加载函数
def load_data(path):
data = loadmat(path)
X = data['X']
y = data['y']
return X, y
# 加载数据
raw_X, raw_y = load_data('ex3data1.mat')
# 在特征矩阵 X 中插入一列值为1的截距项
X = np.insert(raw_X, 0, 1, axis=1) # 插入后的 X 形状为 (5000, 401)
# 将目标向量 y 展平,使其从 (5000, 1) 变为 (5000,)
y = raw_y.flatten() # 或者使用 .reshape(-1) 达到同样效果
# 使用 one_vs_all 函数训练多类别逻辑回归模型
# 参数为 X, y, 正则化参数 lambda=1, 类别数量 K=10
all_theta = one_vs_all(X, y, 1, 10)
# 输出训练好的参数,每一行对应一个分类器的一组参数
all_theta # 每一行是一个分类器的一组参数
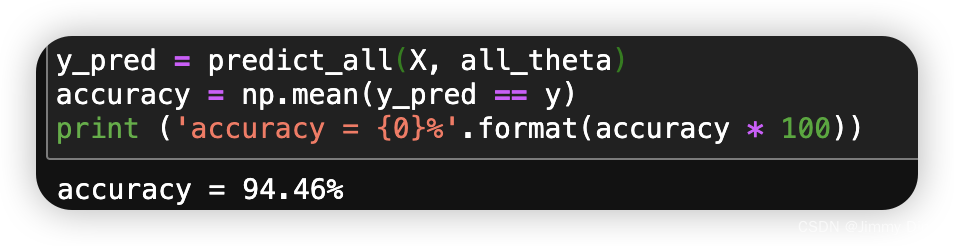
y_pred = predict_all(X, all_theta)
accuracy = np.mean(y_pred == y)
print ('accuracy = {0}%'.format(accuracy * 100))
2.神经网络
在本练习的前一部分中,您实现了多类逻辑回归来识别手写数字。但是,逻辑回归不能形成更复杂的假设,因为它只是一个线性分类器。在本练习的这一部分中,您将使用与之前相同的训练集来实现一个神经网络来识别手写数字。神经网络将能够表示形成非线性假设的复杂模型。本周,您将使用我们已经训练过的神经网络中的参数。您的目标是实现前馈传播算法以使用我们的权重进行预测。
2.1模型表示
我们的神经网络如图 2 所示。它有 3 层——输入层、隐藏层和输出层。回想一下,我们的输入是数字图像的像素值。由于图像的大小为 20×20,因此我们有 400 个输入层单元(不包括始终输出 +1 的额外偏置单元)。与之前一样,训练数据将加载到变量 X 和 y 中。
我们已为您提供一组经过训练的网络参数(Θ(1)、Θ(2))。这些参数存储在 ex3weights.mat 中,并将由 ex3 nn.m 加载到 Theta1 和 Theta2 中。这些参数的尺寸适合第二层有 25 个单元和 10 个输出单元(对应 10 个数字类别)的神经网络。

现在,您将为神经网络实现前馈传播。您需要完成 predict.m 中的代码以返回神经网络的预测。您应该实现前馈计算,为每个示例 i 计算 hθ(x(i)) 并返回相关预测。与一对多分类策略类似,神经网络的预测将是具有最大输出 (hθ(x))k 的标签。
def load_weight(path):
"""
从.mat文件加载神经网络的权重数据
参数:
path: 文件路径
返回:
Theta1, Theta2: 神经网络的权重矩阵
"""
data = loadmat(path) # 加载.mat文件
return data['Theta1'], data['Theta2'] # 返回权重矩阵 Theta1 和 Theta2
# 从指定路径加载神经网络的权重数据
theta1, theta2 = load_weight('ex3weights.mat')
# 输出权重矩阵的形状
theta1.shape, theta2.shape # 返回 (25, 401), (10, 26)
def load_data(path):
"""
从.mat文件加载数据
参数:
path: 文件路径
返回:
X: 特征矩阵
y: 目标向量
"""
data = loadmat(path) # 加载.mat文件
X = data['X'] # 提取特征矩阵
y = data['y'] # 提取目标向量
return X, y # 返回特征矩阵和目标向量
# 加载数据
X, y = load_data('/ex3data1.mat')
# 将目标向量 y 展平,使其从 (5000, 1) 变为 (5000,)
y = y.flatten() # 展平目标向量,变为一维数组 (5000,)
# 在特征矩阵 X 中插入一列值为1的截距项
X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1) # 插入第一列为1的截距项,形状变为 (5000, 401)
# 输出特征矩阵和目标向量的形状
X.shape, y.shape # 返回 ((5000, 401), (5000,))
def load_data(path):
"""
从.mat文件加载数据
参数:
path: 文件路径
返回:
X: 特征矩阵
y: 目标向量
"""
data = loadmat(path) # 加载.mat文件
X = data['X'] # 提取特征矩阵
y = data['y'] # 提取目标向量
return X, y # 返回特征矩阵和目标向量
# 加载数据
X, y = load_data('ex3data1.mat')
# 将目标向量 y 展平,使其从 (5000, 1) 变为 (5000,)
y = y.flatten() # 展平目标向量,变为一维数组 (5000,)
# 在特征矩阵 X 中插入一列值为1的截距项
X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1) # 插入第一列为1的截距项,形状变为 (5000, 401)
# 输出特征矩阵和目标向量的形状
X.shape, y.shape # 返回 ((5000, 401), (5000,))
# 前向传播步骤
a1 = X
# 计算隐藏层输入 z2
z2 = a1 @ theta1.T # (5000, 401) @ (25, 401).T => (5000, 25)
z2.shape # 输出 (5000, 25)
# 插入截距项
z2 = np.insert(z2, 0, 1, axis=1) # (5000, 26)
# 计算隐藏层输出 a2
a2 = sigmoid(z2)
a2.shape # 输出 (5000, 26)
# 计算输出层输入 z3
z3 = a2 @ theta2.T # (5000, 26) @ (10, 26).T => (5000, 10)
z3.shape # 输出 (5000, 10)
# 计算输出层输出 a3
a3 = sigmoid(z3)
a3.shape # 输出 (5000, 10)
# 预测标签
y_pred = np.argmax(a3, axis=1) + 1 # 预测的标签,从0开始索引,所以需要加1
# 计算准确率
accuracy = np.mean(y_pred == y)
print('accuracy = {0}%'.format(accuracy * 100)) # 输出准确率,结果为97.52%
总结(自己训练求解参数全流程)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
from scipy.optimize import minimize
# 加载数据函数
def load_data(path):
data = loadmat(path)
X = data['X']
y = data['y']
return X, y
# Sigmoid函数
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 正则化成本函数
def regularized_cost(theta, X, y, l):
thetaReg = theta[1:]
first = (-y * np.log(sigmoid(X @ theta))) + (y - 1) * np.log(1 - sigmoid(X @ theta))
reg = (thetaReg @ thetaReg) * l / (2 * len(X))
return np.mean(first) + reg
# 正则化梯度函数
def regularized_gradient(theta, X, y, l):
thetaReg = theta[1:]
first = (1 / len(X)) * X.T @ (sigmoid(X @ theta) - y)
reg = np.concatenate([np.array([0]), (l / len(X)) * thetaReg])
return first + reg
# one_vs_all函数
def one_vs_all(X, y, l, K):
all_theta = np.zeros((K, X.shape[1])) # 初始化参数矩阵
for i in range(1, K + 1):
theta = np.zeros(X.shape[1])
y_i = np.array([1 if label == i else 0 for label in y]) # 转换标签
ret = minimize(fun=regularized_cost, x0=theta, args=(X, y_i, l), method='TNC', jac=regularized_gradient, options={'disp': True})
all_theta[i - 1, :] = ret.x # 存储训练好的参数
return all_theta
# 预测函数
def predict_all(X, all_theta):
h = sigmoid(X @ all_theta.T)
h_argmax = np.argmax(h, axis=1)
h_argmax = h_argmax + 1
return h_argmax
# 加载数据
raw_X, raw_y = load_data('ex3data1.mat')
# 添加截距项
X = np.insert(raw_X, 0, 1, axis=1) # (5000, 401)
# 展平标签
y = raw_y.flatten() # (5000,)
# 设置正则化参数和类别数量
lambda_ = 1
num_labels = 10
# 训练模型
all_theta = one_vs_all(X, y, lambda_, num_labels)
# 进行预测
y_pred = predict_all(X, all_theta)
# 计算准确率
accuracy = np.mean(y_pred == y) * 100
print(f'accuracy = {accuracy}%')





![[机器学习算法]决策树](https://img-blog.csdnimg.cn/direct/a532fe7466664f8ab129d0b58734aab2.png)