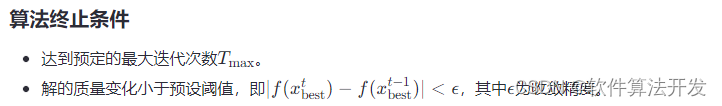理论

椭圆型方程一维格式即常微分方程，边值问题，方程如下所示：

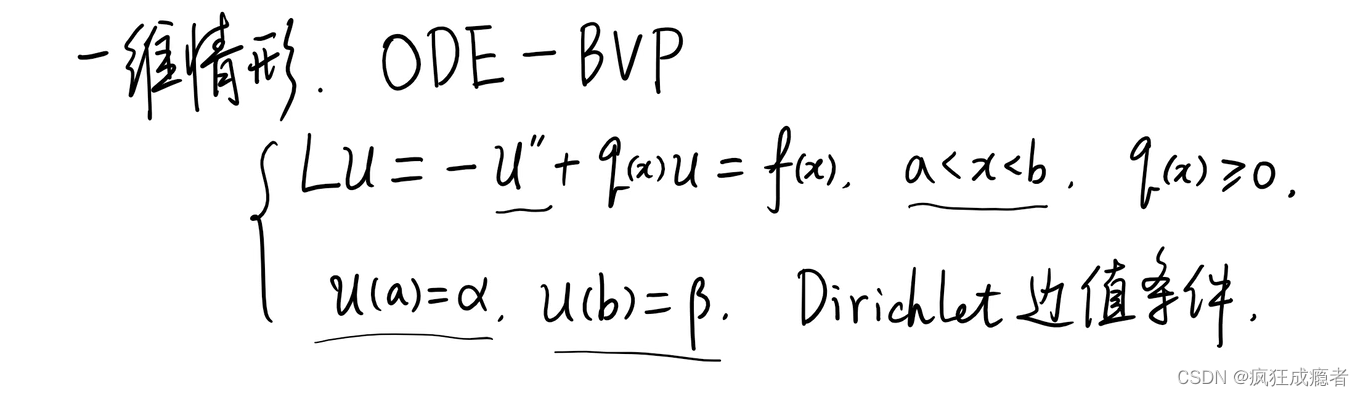
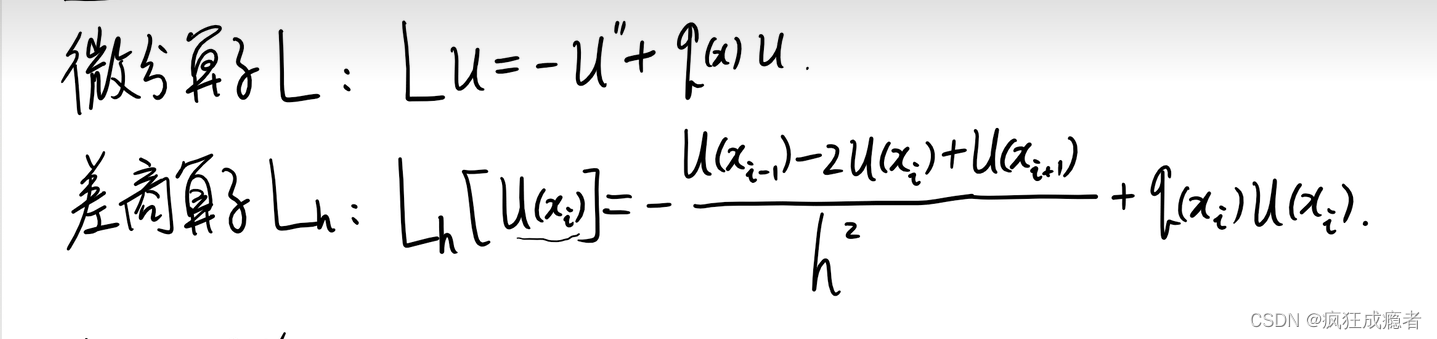
截断误差：

当$h\to \infty$时，截断误差趋于零，离散方程组成立，

写成矩阵：

用离散化方程组求解：

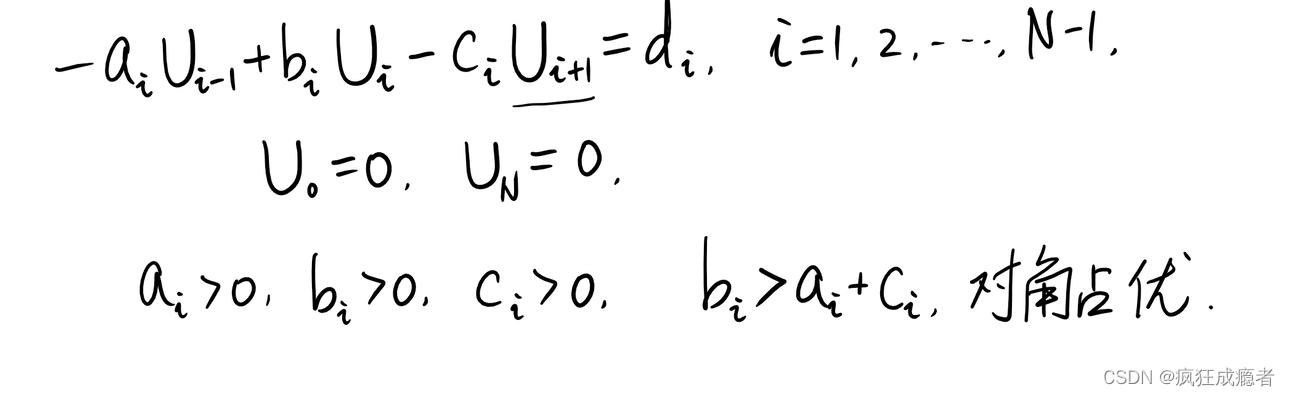
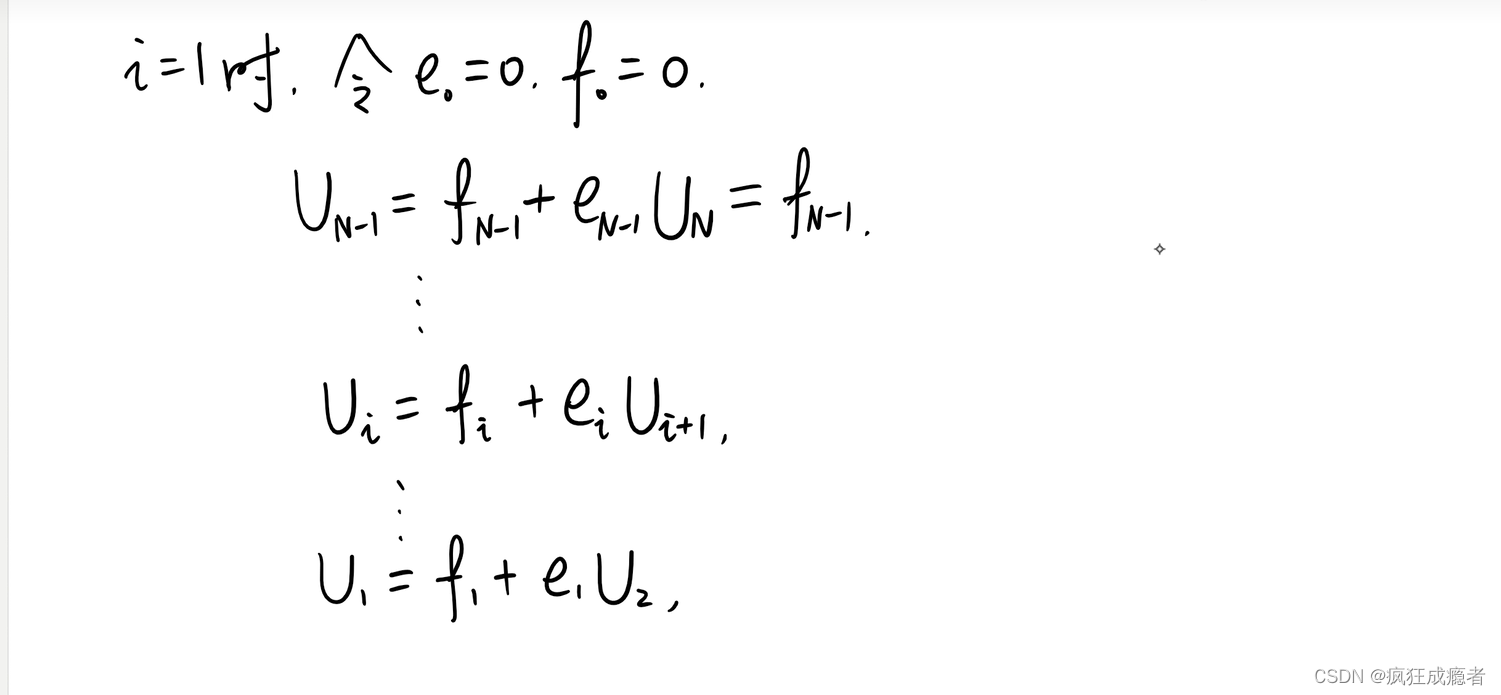
编程实例

对比：

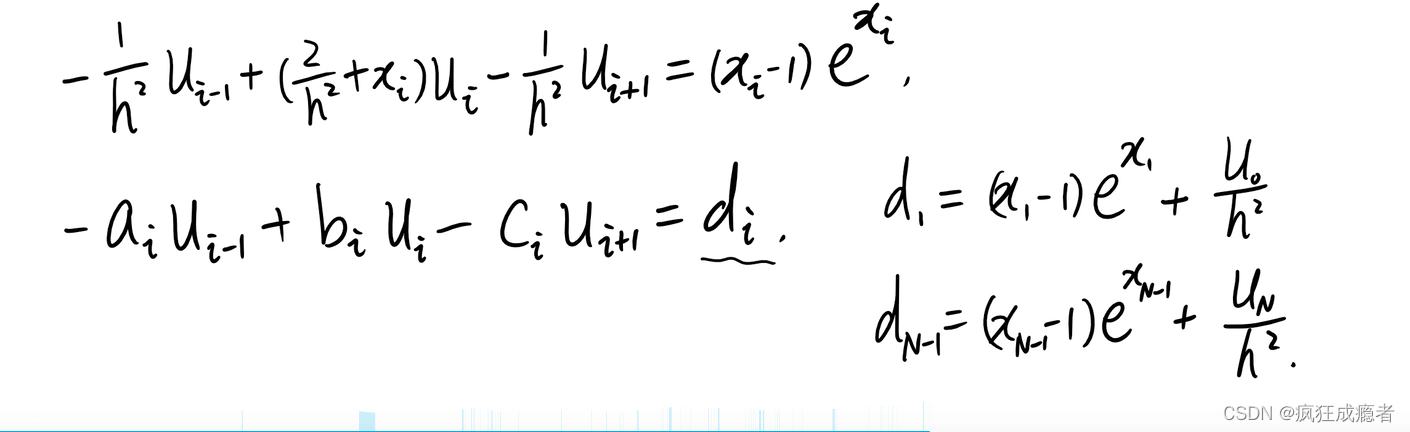
边值条件：

% boundary conditions
u0 = 1;
uN = exp(1);

区域的划分：

% partion of the domain
N = 20;
h = 1/N;
x_all = (0:h:1)';
x = x_all(2:end-1);

代入d：

% the right hand side
d = fx(x);
d(1) = d(1) + u0/h^2;
d(N-1) = d(N-1) + uN/h^2;

其中：

function y = fx (x)
y = (x-1).*exp(x);
end

thomas算法：

% thomas algorithm
u = thomas (a,b,c,d);

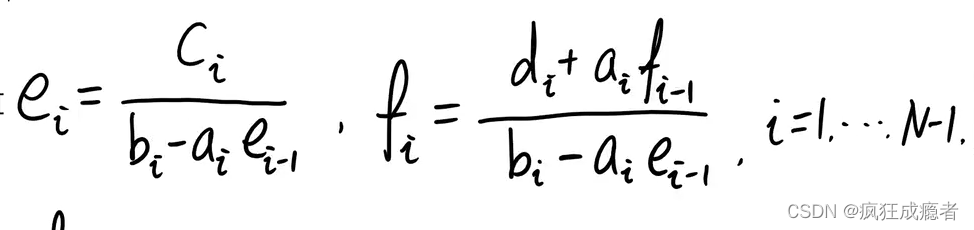
function u = thomas(a, b, c, d)
M = length(a);
u = zeros(M,1);
e = zeros(M,1);
f = zeros(M,1);
e(1) = c(1)/b(1);
f(1) = d(1)/b(1);

% forward
for i = 2:M
    e(i) = c(i)/( b(i)-a(i)*e(i-1));
    f(i) = (d(i)+a(i)*f(i-1))/(b(i)-a(i)*e(i-1));
end

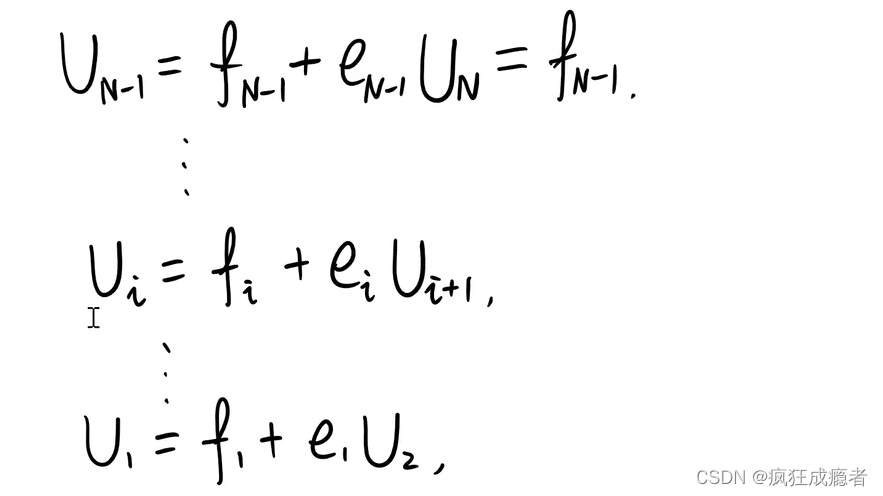
%backward
u(M) = f(M);
for i = M-1:-1:1
    u(i) = f(i) + e(i)*u(i+1);
end
end

计算真解：

% the exact solution
u_e = u_exact(x_all);

原代码

% boundary conditions
u0 = 1;
uN = exp(1);

% partion of the domain
N = 20;
h = 1/N;
x_all = (0:h:1)';
x = x_all(2:end-1);

% the right hand side
d = fx(x);
d(1) = d(1) + u0/h^2;
d(N-1) = d(N-1) + uN/h^2;

% diagonals of the coefficient matrix A
q = qx(x);
a = ones (N-1,1)/h^2;
b = 2*ones (N-1,1)/h^2 + q;
c = a;

% thomas algorithm
u = thomas (a,b,c,d);

% A = spdiags([-a b -c],[-1 0 1],N-1,N-1);
% u = A\d;

% the exact solution
u_e = u_exact(x_all);

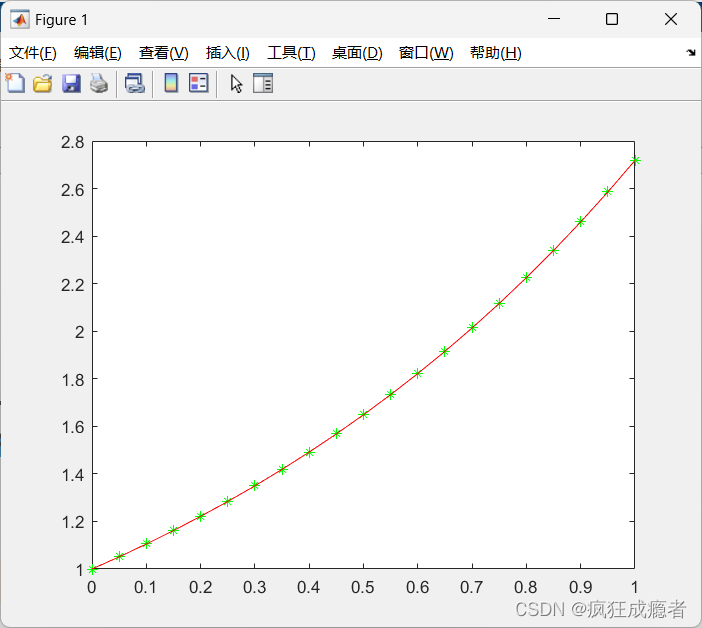
figure(1)
plot(x_all,[u0;u;uN],'g*',x_all,u_e,'r');
% end
%——--subroutines-
function y = qx(x)
y = x;
end
 
function y = fx (x)
y = (x-1).*exp(x);
end

function y = u_exact(x)
y = exp(x);
end

function u = thomas(a, b, c, d)
M = length(a);
u = zeros(M,1);
e = zeros(M,1);
f = zeros(M,1);
e(1) = c(1)/b(1);
f(1) = d(1)/b(1);

% forward
for i = 2:M
    e(i) = c(i)/( b(i)-a(i)*e(i-1));
    f(i) = (d(i)+a(i)*f(i-1))/(b(i)-a(i)*e(i-1));
end

%backward
u(M) = f(M);
for i = M-1:-1:1
    u(i) = f(i) + e(i)*u(i+1);
end
end

输出结果：