引入:在面对线性可分时,即用一条直线就可以区分数据的时候,需要将直线放在距离数据点距离最大化的位置,这个过程需要寻找最大间隔,即为最优化问题。当数据点不能用一根直线区分——线性不可分,就需要用核函数将数据点映射到高维空间运算得到超平面进行区分。
一、基本原理
1、概念
解决二分类问题,通过寻找最优决策面来对数据进行分类。
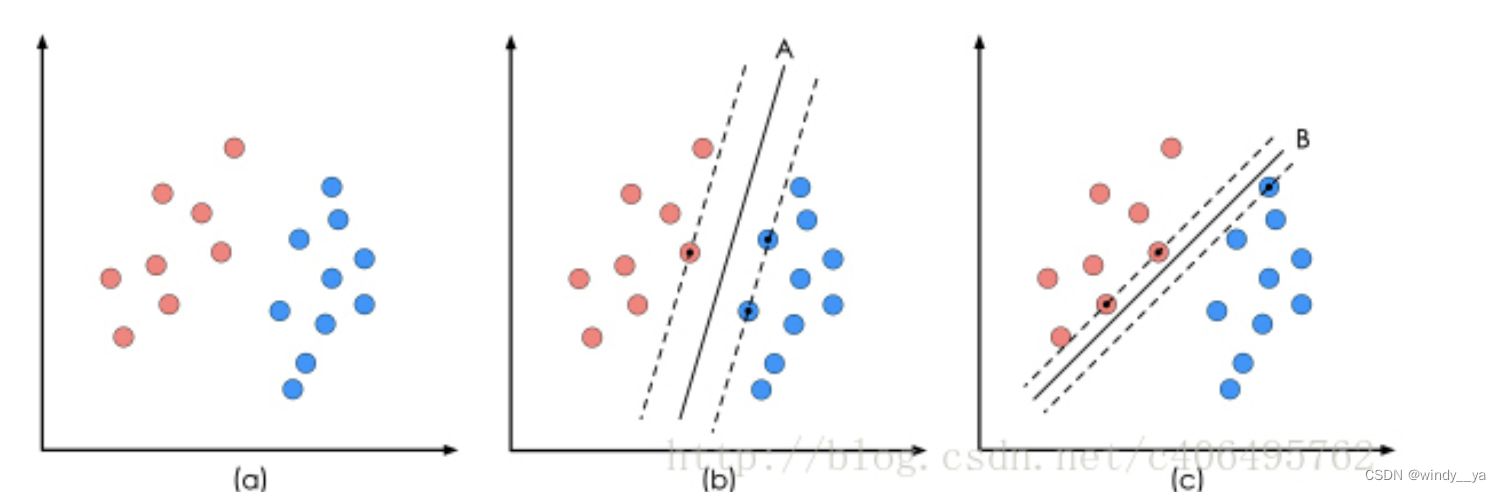
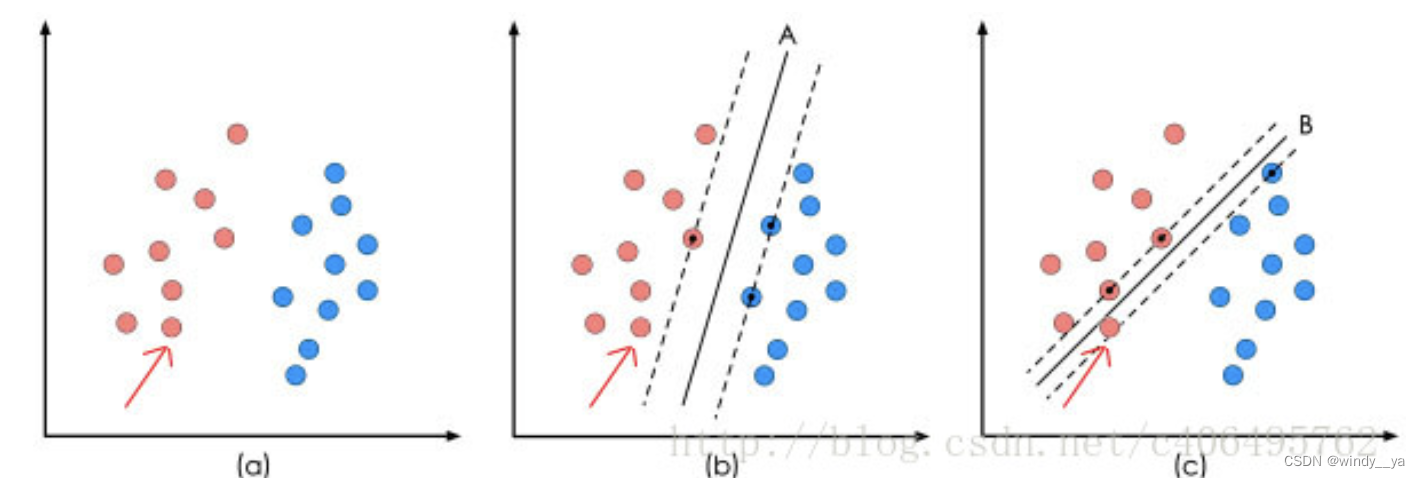
如下图,当分类(a)中的数据点时,(b)和(c)两种都能够正确分类,
但当数据点增加,(b)的分类结果明显好于(c)。显然,同一波数据有不同划分的决策面,但是需要让他的间隔最大从而找出最优决策面,即SVM的最优解。
2、重点名词解释
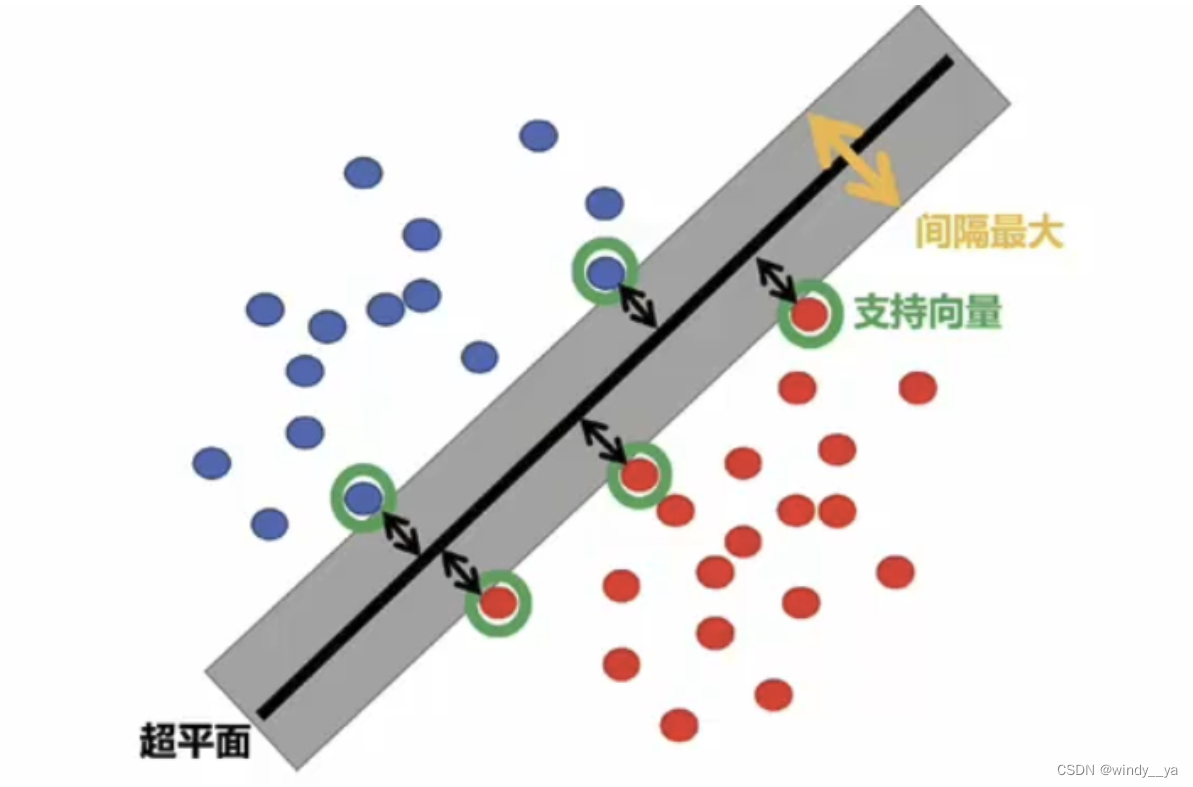
①超平面:将数据点划分为不同类别 —— 维度比当前空间维度低一维,eg二维数据下就是一条直线,三维空间内就是一个平面,n维数据就是n-1维。
②支持向量:位于间隔边界的数据点,即离分隔超平面最近的那些点。是最有可能被错误分类的数据点,直接影响超平面的位置和方向。
③最大间隔:距离是指支持向量到超平面的距离。SVM的目标不只是找到能够正确分类的超平面,还希望这个超平面能有最大间隔,从而让模型更具鲁棒性,不容易受噪声和异常点影响。
3、核函数【针对线性不可分问题】
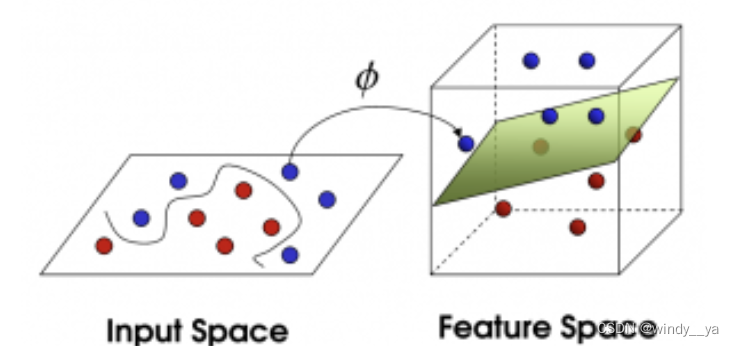
在解决如下图数据点线性不可分的情况下,映射到高维找到决策面。但是这里需要注意,他并不是在高维空间的数据点进行高维空间运算,核函数相当于一个小trick,通过实现在高维空间的效果下在原低维空间内进行运算,从而解决了高维空间内的计算成本。
二、SVM的数学建模
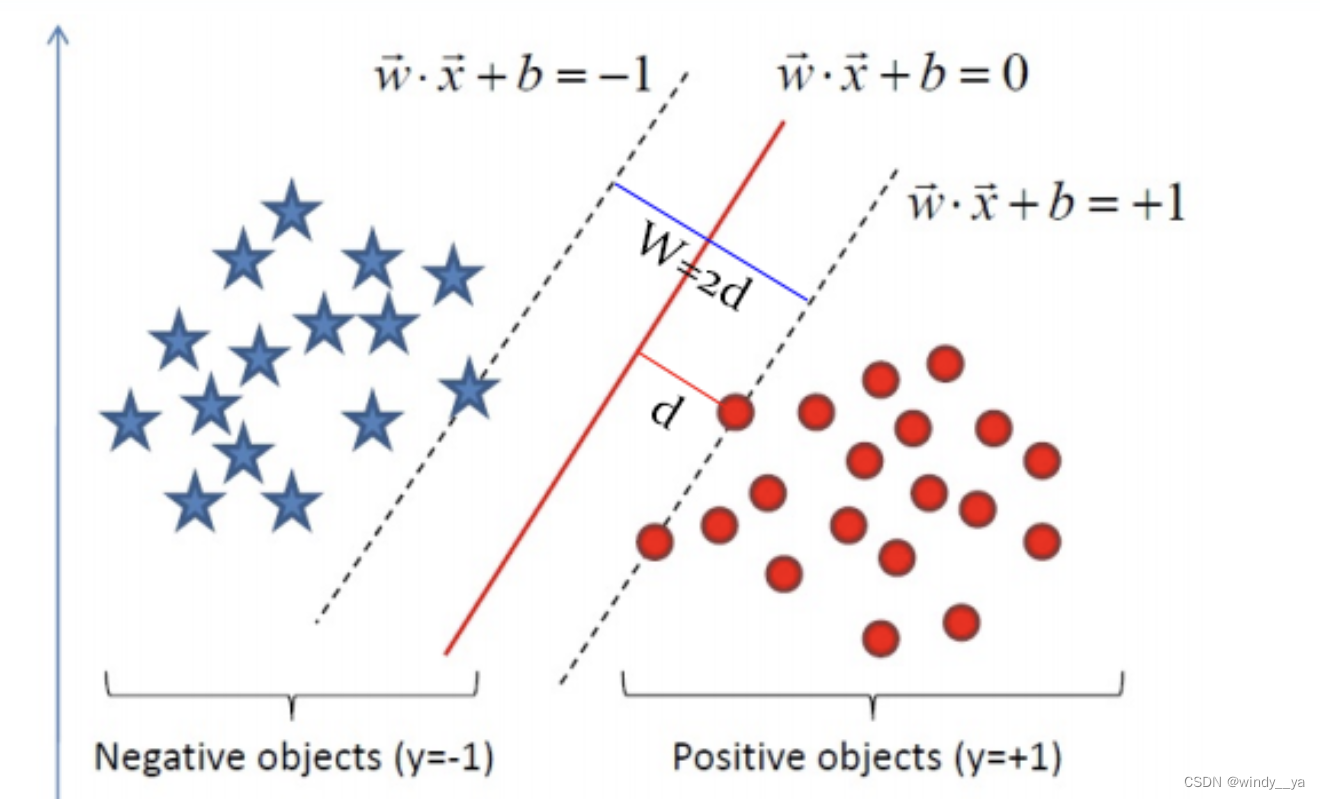
1)首先定义超平面为 w⋅x+b=0,则数据带你到超平面的距离为 ,而我们希望找到这样的超平面使得
—— 该表达式保证数据点位于超平面的正确一侧。
2)目标函数的优化问题:求解间隔最大化
转化一下以下就是求解以下公式,该公式就是SVM的基本模型了
然后就是通过拉格朗日和对偶进行数学推导找到最优的w和b了,公式推导指路SVM公式推导
&s.t.
,和
因为所有的数据并不一定都是“干净”的(即可能存在噪声),因此在这里引入松弛变量 C,用于控制“最大化间隔”和“保证大部分点的函数间隔<1”的权重,允许有些数据点可以分错。
约束条件变成 和
所以,SVM的主要工作就是求解这些
三、SVM简单构造
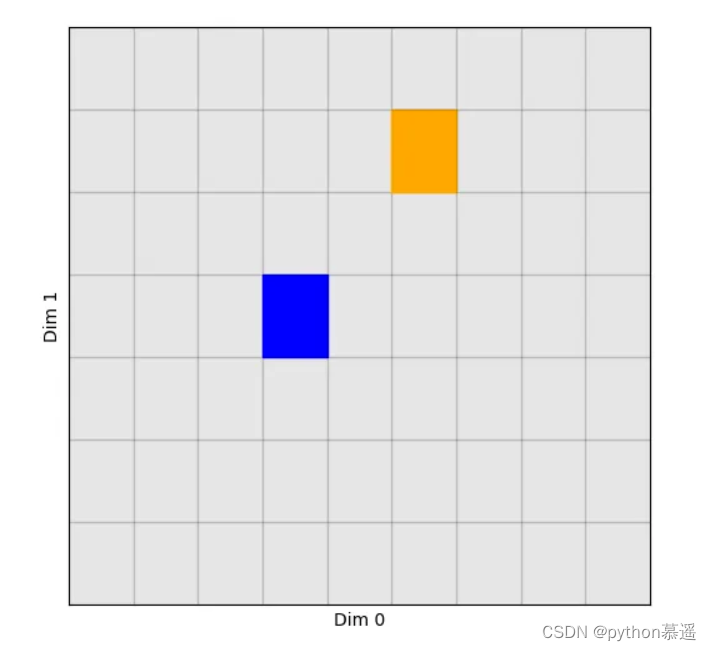
1、准备数据
数据结构如下图
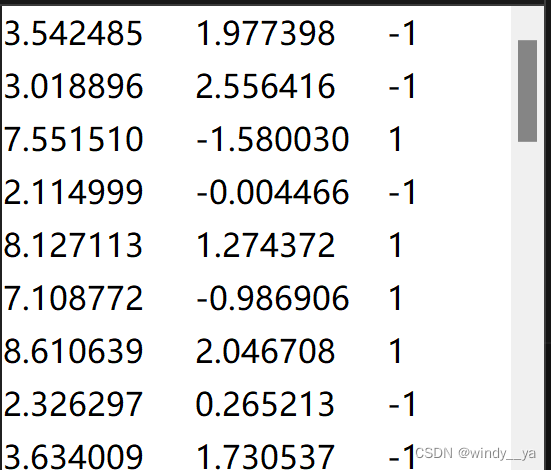
导入数据并进行可视化
import matplotlib.pyplot as plt
import numpy as np
def loadDataSet(fileName):
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines(): #逐行读取,滤除空格等
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])]) #添加数据
labelMat.append(float(lineArr[2])) #添加标签
return dataMat,labelMat
def showDataSet(dataMat, labelMat):
data_plus = [] #正样本
data_minus = [] #负样本
for i in range(len(dataMat)):
if labelMat[i] > 0:
data_plus.append(dataMat[i])
else:
data_minus.append(dataMat[i])
data_plus_np = np.array(data_plus) #转换为numpy矩阵
data_minus_np = np.array(data_minus) #转换为numpy矩阵
plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1]) #正样本散点图
plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1]) #负样本散点图
plt.show()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet('testSet.txt')
showDataSet(dataMat, labelMat)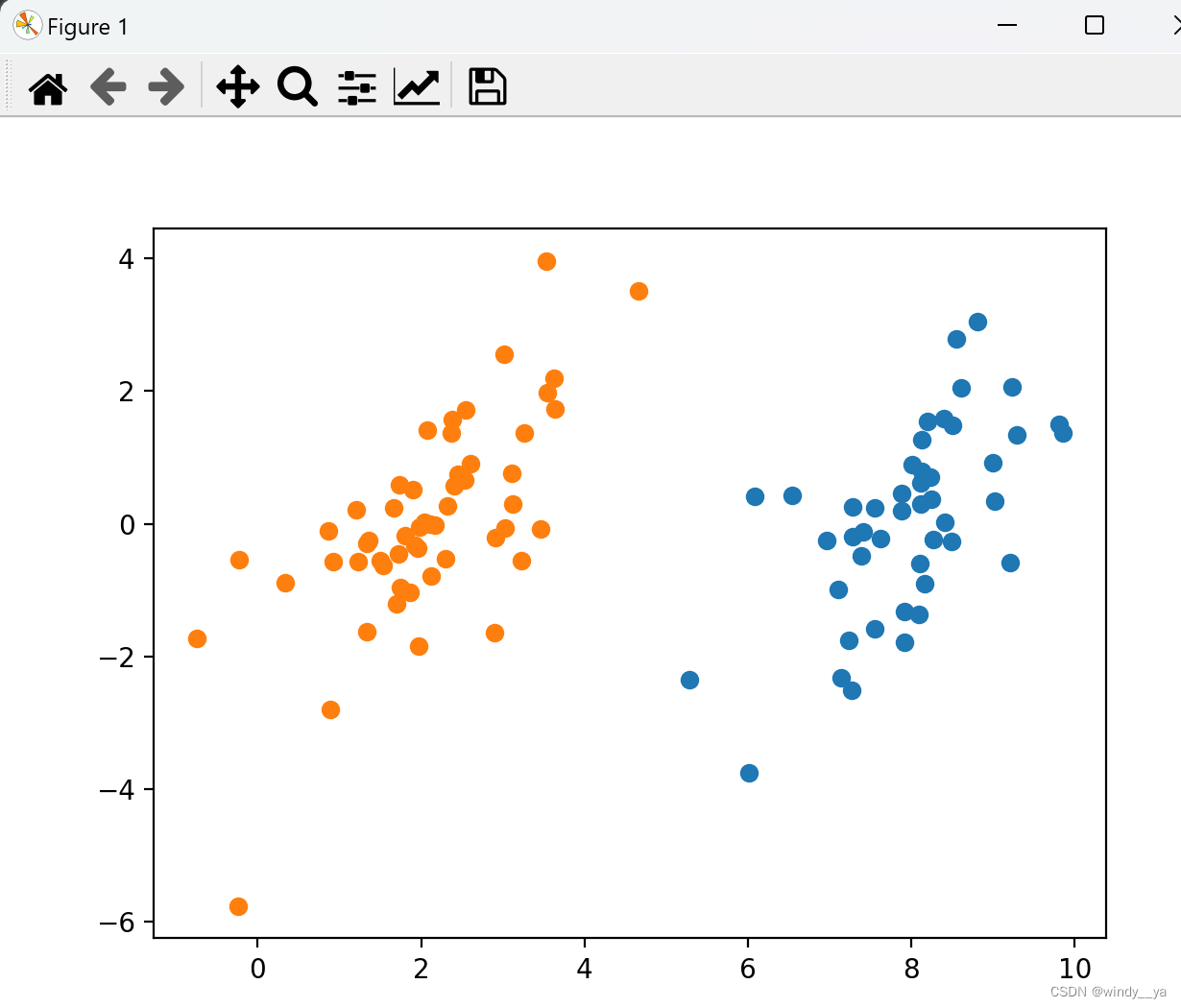
2、SVM 函数定义
class mySVM:
def __init__(self, learning_rate=0.01, lambda_param=0.1, n_iters=1000):
self.learning_rate = learning_rate
self.lambda_param = lambda_param
self.n_iters = n_iters
self.w = None
self.b = None
def fit(self, X, y):
n_samples, n_features = X.shape
self.w = np.zeros(n_features)
self.b = 0.0
for _ in range(self.n_iters):
linear_output = np.dot(X, self.w) - self.b
errors = y - linear_output
self.w -= self.learning_rate * (2 * self.lambda_param * self.w - np.dot(X.T, errors))
self.b -= self.learning_rate * np.mean(errors)
def predict(self, X):
linear_output = np.dot(X, self.w) - self.b
return np.sign(linear_output)
def loss(self, X, y):
linear_output = np.dot(X, self.w) - self.b
hinge_loss = np.maximum(0, 1 - y * linear_output)
reg_loss = self.lambda_param * np.linalg.norm(self.w)
return np.mean(hinge_loss) + 0.5 * reg_loss3、绘制数据点和决策边界
# 可视化数据点和决策边界
def plot_show(X, y, svm):
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=20, edgecolor='k')
# 创建一个网格
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
# 计算决策边界,Z 是一个二维网格,表示每个点属于哪个类别
Z = svm.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 绘制决策边界
plt.contourf(xx, yy, Z, alpha=0.4, cmap=plt.cm.coolwarm)
plt.contour(xx, yy, Z, colors='k', linestyles='-', levels=[0])
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('SVM Decision Boundary')
plt.show()4、结果展示
# 主程序
if __name__ == "__main__":
fileName = 'testSet.txt'
dataMat, labelMat = loadDataSet(fileName)
# 实例化并训练SVM模型
svm = mySVM(learning_rate=0.01, lambda_param=0.1, n_iters=1000)
svm.fit(dataMat, labelMat)
# 绘制决策边界
plot_show(dataMat, labelMat, svm)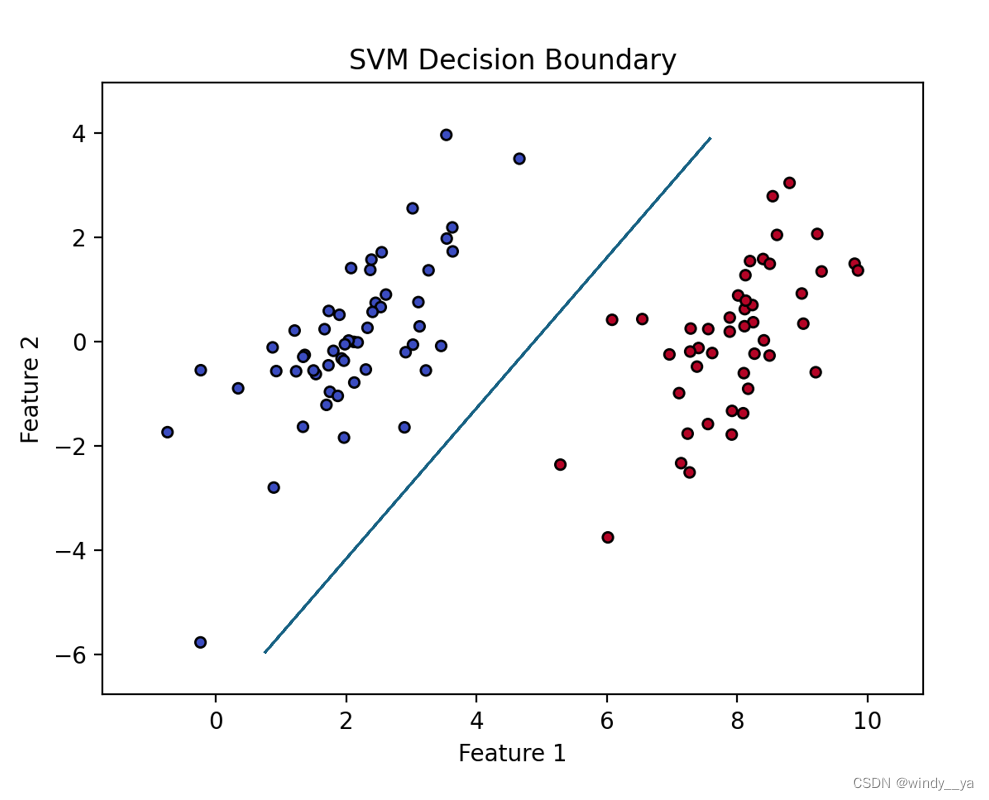
四、总结
上面用到的是线性SVM,但在实际应用中,需要处理更复杂的数据分布,例如使用核函数处理非线性可分的数据。此外,超参数的选择(如学习率、正则化参数和迭代次数)对模型性能有重要影响,还有松弛变量C对最后模型的训练效果也有很大影响(可能存在过拟合/欠拟合)
SVM的优缺点
- 优点:高准确率,对高维数据有效等
- 缺点:对核函数和参数选择敏感,计算复杂度高等