A Alice and books 

题目：

思路：编号最大的肯定会被读到，所以在编号最大的这一组书中不能存在除去最大编号的外书外页数最大的书，并且在另一堆中这本书的编号也应该是最大值

代码：

#include <iostream>

using namespace std;

const int N = 110;

int n, a[N];

void solve() {
    cin >> n;
    for(int i = 1; i <= n; i ++ ) cin >> a[i];
    int ans = a[n];
    int res = 0;
    for(int i = 1; i <= n - 1; i ++ ) {
        res = max(res, a[i]);
    }
    cout << res + ans << endl;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while(t -- ) {
        solve();
    }
    return 0;
}

B new bakery

问题：

思路：列出profit表达式后发现该表达式是二次函数，于是问题变成了求二次函数的最值，注意取值范围，求最值这个简单啊，模拟退火，爬山，这里是最简单的分类讨论。

代码：

#include <iostream>

using namespace std;

long long a, n, b;

void solve() {
    cin >> a >> n >> b;
    long long ans = 0;
    long long k = 0;
    if(min(n, b) <= (b - a)) {
        k = min(n, b);
        ans = k * (b + 1) - (k + 1) * k / 2 + a * (n - k);
    } else {
        k = b - a;
        ans = k * (b + 1) - (k + 1) * k / 2 + a * (n - k);
        long long res = 0;
        k ++;
        res = k * (b + 1) - (k + 1) * k / 2 + a * (n - k);
        ans = max(res, ans);
    }
    cout << ans << endl;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while(t -- ) {
        solve();
    }
    return 0;
}

C manhattan permutations

问题：

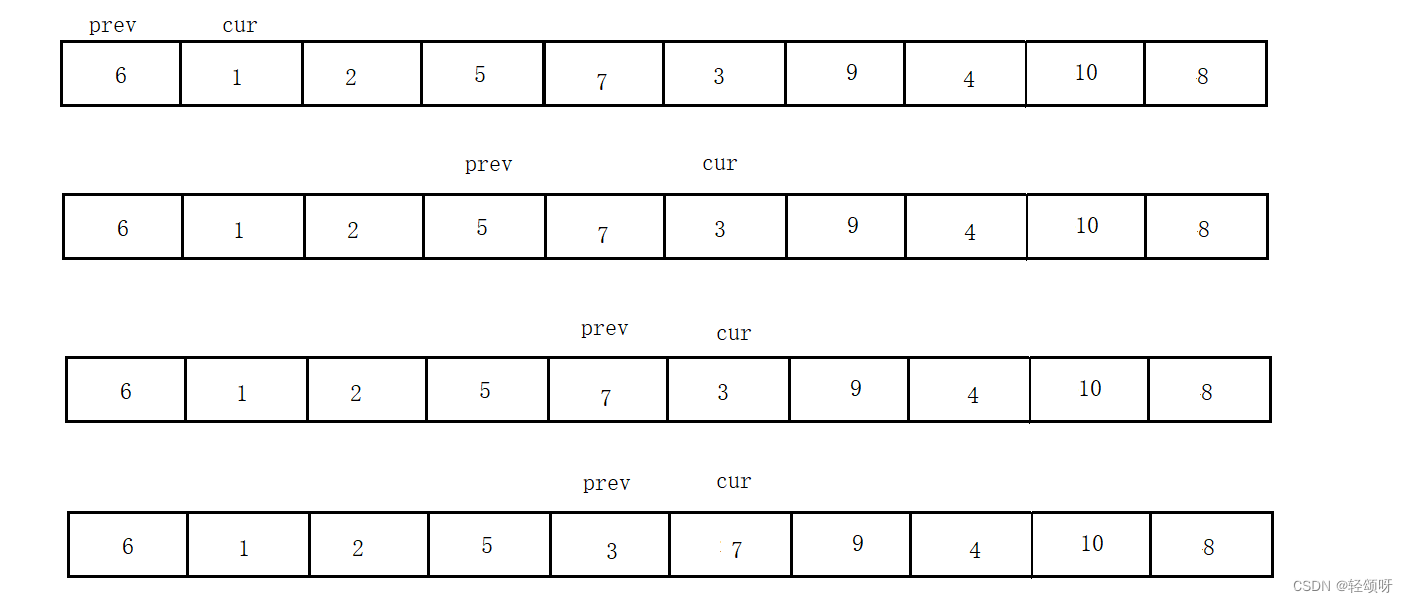
思路：不难发现，假设最开始我们的答案permutation与原有序permutation一致，此时如果交换相邻元素会使得最终结果add 2如果岔开一个交换会使得结果add 4...类推后发现交换i，j号元素会使得结果add 2 * (j - i)。因此在构造序列时，我们可以先从当前可以选择交换的最大值的开始构造，即先交换可以交换的最远距离，若第一次交换i,j那么第二次的交换区间就变成了在(i +1)到(j - 1)内重复第一次交换的操作。现在感性的证明一下该结论主要证明的点是为什么要缩小范围，假设第一次交换为i，j。第二次交换为i + 1, j + 1两次交换总共使得答案增加了 (j - i) * 4 则说明第一次交换我们找到的点并不是最远可以交换的点。因此结论正确。注意，这里只是感性的理解，并不是理性的证明

代码：

#include <bits/stdc++.h>

using namespace std;

int n;
long long k;

void solve() {
   cin >> n >> k;
   long long tmp = k;
   vector<int> a(n + 1);
   vector<bool> st(n + 1, false);
   for(int i = 1; i <= n; i ++ ) a[i] = i;
   long long up = 0;
    for(int i = 1; i <= n + 1 >> 1; i ++ ) {
        up += abs(n - i + 1 - i) * 2;
    }

    if(k > up || k & 1) {
        cout << "No" << endl;
        return;
    }
    
    for(int i = 1, last = n; i <= n && k != 0 && i <= last; i ++ ) {
        int l = i, r = last;
        while(l < r) {
            int mid = l + r + 1 >> 1;
            if((mid - i) * 2 <= k) l = mid;
            else r = mid - 1;
        }
        swap(a[i], a[l]);
        k -= (l - i) * 2;
        last = l - 1;
        //cout << k << " ";
    }
    long long s = 0;
    for(int i = 1; i <= n; i ++ ) {
        s += abs(i - a[i]);
    }

    if(s != tmp) {
        cout << "No" << endl;
        return;
    }
    cout << "Yes" << endl;
    for(auto t: a) {
        if(t == 0) continue;
        cout << t << " ";
    }
    cout << endl;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while(t -- ) {
        solve();
    }
    return 0;
}