头歌资源库（11）分解2019

news2024/10/5 13:09:35

一、问题描述

二、算法思想

首先，确定第一个整数的范围，由于不能包含数字2和4，所以第一个整数的取值范围为[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 5, 6, 7, 8, 9]。

然后，在确定第一个整数的情况下，确定第二个整数的取值范围，由于不能包含数字2和4，以及第二个整数不能与第一个整数相同，所以第二个整数的取值范围为[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 5, 6, 7, 8, 9]去除第一个整数的值。

最后，在确定前两个整数的情况下，第三个整数的取值范围为[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 5, 6, 7, 8, 9]去除前两个整数的值。

然后，使用递归来遍历所有情况，并计算符合条件的分解方法的数量。

三、代码实现

#include<stdio.h>
int isValidNumber(int n){
    while(n>0){
        if(n%10==2||n%10==4){
            return 0;
        }
        n/=10;
    }
    return 1;
}
int countValidSums(int total){
    int count=0;
    for(int i=1;i<total;i++)
    for(int j=1;j<total;j++){
        int k=total-i-j;
        if(k>j&&isValidNumber(i)&&isValidNumber(j)&&isValidNumber(k)&&j>i){
            count++;
        }
    }

return count;
}
int main()
{
    int result=countValidSums(2019);
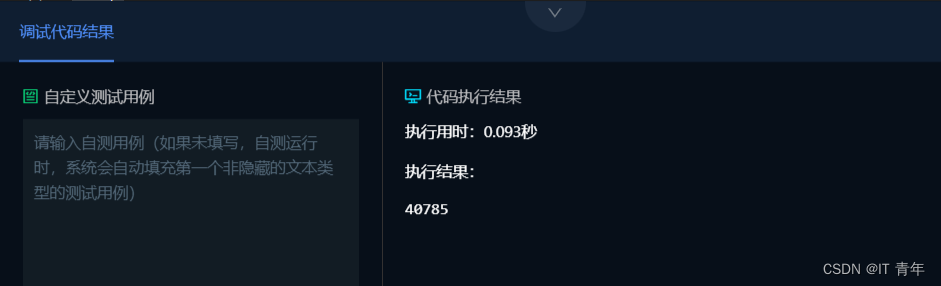
    printf("%d\n",result);
    return 0;
}