【因果推断python】42_异质干预效应2

预测弹性

关键思想

预测弹性

我们在这里陷入了复杂的境地。我们已经同意我们需要预测 $\frac{\delta Y_i}{\delta T_i}$ ，遗憾的是这是不可观察的。因此，我们不能使用 ML 算法并将其作为目标插入。但也许我们不需要观察 $\frac{\delta Y_i}{\delta T_i}$ 来预测它

这是一个想法。如果我们使用线性回归呢？

假设您将以下线性模型拟合到您的数据中。

$y_i=\beta_0+\beta_1t_i+\beta_2X_i+e_i$

如果你在干预变量上区分它，你最终会得到

$\frac{\delta y_i}{\delta t_i}=\beta_1$

既然你可以估计上面的模型得到 $\hat{\beta}_{1}$ ，我们甚至可以大胆地说即使你无法观察到弹性，你也可以预测它。在上面的例子中，这是一个相当简单的预测，即我们为每个人预测常数值 $\hat{\beta}_{1}$ 。那是一些东西，但还不是我们想要的。那是ATE，不是CATE。这无助于我们根据实体对干预的反应程度对实体进行分组的任务，因为每个人都得到相同的弹性预测。但是，我们可以做以下简单的改变

$y_i=\beta_0+\beta_1t_i+\beta_2X_i+\beta_3t_iX_i+e_i$

这反过来会给我们以下弹性预测

$\widehat{\frac{\delta y_i}{\delta t_i}}=\hat{\beta_1}+\hat{\beta_3}X_i$

其中 $\beta_{3}$ 是 X 中特征的向量系数。

现在由不同的 $X_{i}$ 定义的每个实体将有不同的弹性预测。换句话说，弹性预测会随着 X 的变化而变化。唉，回归可以为我们提供一种估计 CATE $E[y^{'}(t)|X]$ 的方法。

我们终于到了某个地方。上面的模型允许我们对每个实体进行弹性预测。通过这些预测，我们可以创建更多有用的组。我们可以将具有高预测弹性的单元组合在一起。我们可以对预测弹性低的那些做同样的事情。最后，通过我们的弹性预测，我们可以根据我们认为实体对干预的反应程度对它们进行分组。

理论到此为止。是时候通过一个示例来说明如何制作这种弹性模型了。让我们考虑一下我们的冰淇淋示例。每个单位 i 是一天。对于每一天，我们都知道是否是工作日，制作冰淇淋的成本是多少（您可以将成本视为质量的代表）以及当天的平均温度。这些将是我们的特征空间 X。然后，我们有我们的干预手段、价格和我们的结果，即售出的冰淇淋数量。对于这个例子，我们将考虑随机处理，这样我们现在不必担心偏差。

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt

import seaborn as sns
import statsmodels.formula.api as smf
import statsmodels.api as sm

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split
prices_rnd = pd.read_csv("./data/ice_cream_sales_rnd.csv")
print(prices_rnd.shape)
prices_rnd.head()
(5000, 5)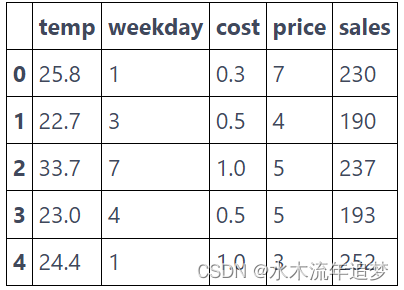

请记住我们的目标：我们需要根据具体的“功能”、“临时”、“工作日”和“成本”来决定何时收取更多费用以及何时收取更少费用。如果这是目标，则需要评估干预效果异质性模型在实现该目标方面的有用性。我们稍后会谈到这一点（下一章会详细介绍）。现在，让我们将数据集拆分为训练和测试集。

np.random.seed(123)
train, test = train_test_split(prices_rnd)

现在我们有了训练数据，我们需要建立一个模型，让我们能够区分价格弹性高的日子和价格弹性低的日子。我们这样做的方法是简单地预测价格弹性。具体如何？首先，让我们考虑使用以下线性模型

$sales_i=\beta_0+\beta_1price_i+\boldsymbol{\beta_2}X_i+e_i$

如果我们检查这个模型的参数，我们可以看到我们预测的弹性会是什么样子。

m1 = smf.ols("sales ~ price + temp+C(weekday)+cost", data=train).fit()
m1.summary().tables[1]

对于 m1，预测的价格弹性 $\widehat{\frac{\delta y_i}{\delta t_i}}$ 将由 $\hat{\beta_1}$ ，在我们的例子中是 -2.75。这意味着，我们为冰淇淋收取的每额外巴西雷亚尔，我们预计销售额将下降约 3 个单位。

注意这个 m1 如何为每个人预测完全相同的弹性。因此，如果我们想知道人们在哪些日子对冰淇淋价格不那么敏感，这不是一个很好的模型。当我们在这里需要的是 CATE 时，它会估计 ATE。请记住，我们的目标是以这样一种方式对实体进行分区，以便我们可以针对每个单独的分区个性化和优化我们的处理（价格）。如果每个预测都相同，我们就无法进行分区。我们没有区分敏感单位和非敏感单位。为了纠正这一点，考虑我们的第二个模型：

$sales_i=\beta_0+\beta_1price_i+\beta_2price_i*temp_i*+\boldsymbol{\beta_3}X_i+e_i$

第二个模型包括价格和温度之间的交互项。这意味着它允许弹性在不同温度下有所不同。我们在这里实际上要说的是，人们对价格上涨或多或少敏感，具体取决于温度。

m2 = smf.ols("sales ~ price*temp + C(weekday) + cost", data=train).fit()
m2.summary().tables[1]

一旦我们估计模型，预测的弹性由下式给出

$\frac{\delta\widehat{sales}_{i}}{\delta price_{i}}=\hat{\beta_{1}}+\hat{\beta_{3}}temp_{i}$

请注意， $\hat{\beta}_3$ 为正 0,03，基线弹性 $\beta_{1}$ （在 $0C^{o}$ 处的弹性）为 -3.6。这意味着，平均而言，随着我们提高价格，销售额下降，这是有道理的。这也意味着温度每升高一度，人们对冰淇淋价格上涨的敏感度就会降低（尽管幅度不大）。例如，在 $25C^{o}$ ，我们每多收取一次巴西雷亚尔，我们的销售额就会下降 2.8 个单位 (−3.6+(0.03∗25))(−3.6+(0.03∗25))。但是在 $35C^{o}$ ，我们每多收取一次巴西雷亚尔，它们只会下降 2.5 个单位 (−3.6+(0.03∗35))(−3.6+(0.03∗35))。这也是一种直觉。随着天气越来越热，人们愿意为冰淇淋支付更多费用。

我们可以走得更远。下一个模型包括所有特征空间的交互项。这意味着弹性会随着温度、星期几和成本而变化。 $sales_{i}=\beta_{0}+\beta_{1}price_{i}+\boldsymbol{\beta_{2}X_{i}}*price_{i}+\boldsymbol{\beta_{3}}X_{i}+e_{i}$

m3 = smf.ols("sales ~ price*cost + price*C(weekday) + price*temp", data=train).fit()

根据上述模型，单位水平弹性或 CATE 将由下式给出

其中 $\beta_{1}$ 是价格系数， $\beta_{2}$ 是交互系数的向量。

最后，让我们看看如何实际做出这些弹性预测。一种方法是从模型中提取弹性参数并使用上面的公式。但是，我们将采用更一般的近似值。由于弹性只不过是干预结果的导数，我们可以使用导数的定义。

$\frac{\delta y}{\delta t}=\frac{y(t+\epsilon)-y(t)}{(t+\epsilon)-t}$

随着 ϵ 变为零。我们可以通过将 ϵ 替换为 1 来近似这个定义。

$\frac{\delta y}{\delta t}$ 近似 $\hat{y}(t+1)-\hat{y}(t)$

其中 $\hat{y}$ 由我们模型的预测给出。换句话说，我将用我的模型做出两个预测：一个传递原始数据，另一个传递原始数据，但处理增加一个单位。这些预测之间的差异是我的 CATE 预测。

下面，您可以看到执行此操作的函数。由于我们使用了训练集来估计我们的模型，我们现在将对测试集进行预测。首先，让我们使用我们的第一个 ATE 模型 m1。

def pred_elasticity(m, df, t="price"):
    return df.assign(**{
        "pred_elast": m.predict(df.assign(**{t:df[t]+1})) - m.predict(df)
    })

pred_elasticity(m1, test).head()

使用 m1 进行弹性预测并不好玩。我们可以看到它预测了所有日子的完全相同的值。那是因为该模型上没有交互项。但是，如果我们使用 m3 进行预测，它会为每天输出不同的弹性预测。那是因为现在，弹性或干预效果取决于当天的具体特征。

pred_elast3 = pred_elasticity(m3, test)

np.random.seed(1)
pred_elast3.sample(5)

请注意预测是如何从 -9 变为 1 的数字。这些不是销售列的预测，其数量级为数百。相反，这是一个预测，如果我们将价格提高一个单位，销售额会发生多少变化。在赌注之外，我们可以看到一些奇怪的数字。例如，看一下第 4764 天。它预测的是正弹性。换句话说，我们预测如果我们提高冰淇淋的价格，销售额将会增加。这不符合我们的经济意识。可能是模型对该预测进行了一些奇怪的外推。幸运的是，您不必为此担心太多。请记住，我们的最终目标是根据单位对干预的敏感程度来划分单位。不是提出有史以来最准确的弹性预测。对于我们的主要目标，如果弹性预测根据单元的敏感程度对单元进行排序就足够了。换句话说，即使像 1.1 或 0.5 这样的正弹性预测没有多大意义，我们所需要的只是排序正确，也就是说，我们希望预测为 1.1 的单位比单位受价格上涨的影响更小预测为 0.5。

好的，我们有弹性或 CATE 模型。但仍然存在一个潜在的问题：它们与 ML 预测模型相比如何？现在让我们试试吧。我们将使用机器学习算法，使用价格、温度、工作日和成本作为特征 X 并尝试预测冰淇淋销售。

X = ["temp", "weekday", "cost", "price"]
y = "sales"
ml = GradientBoostingRegressor()
ml.fit(train[X], train[y])

# make sure the model is not overfiting.
ml.score(test[X], test[y])

0.9124088322890127

该模型可以预测我们每天的销售额。但它适合我们真正想要的吗？换句话说，这个模型能区分人们对冰淇淋价格更敏感的日子吗？它可以帮助我们根据价格敏感度决定收取多少费用吗？

要查看哪个模型更有用，让我们尝试使用它们来分割个体单元。对于每个模型，我们将个体单元分成 2 组。我们希望一个群体对价格上涨反应灵敏，而另一个群体则反应不大。如果是这样的话，我们可以围绕这些群体组织我们的业务：对于属于高响应群体的日子，我们最好不要将价格定得太高。对于低响应群体，我们可以提高价格而不会冒太大的销售风险。

bands_df = pred_elast3.assign(
    elast_band = pd.qcut(pred_elast3["pred_elast"], 2), # create two groups based on elasticity predictions 
    pred_sales = ml.predict(pred_elast3[X]),
    pred_band = pd.qcut(ml.predict(pred_elast3[X]), 2), # create two groups based on sales predictions
)

bands_df.head()

接下来，我们需要比较这两个人群分层模型哪一个是最好的。我现在可能有点超前了，因为我们只会在下一章中讨论 CATE 模型评估。但我觉得我可以让你尝尝它的样子。检查这些分层模式有多好的一种非常简单的方法 - 我的意思是好用 - 就是绘制每个分区的销售价格回归线。我们可以通过 Seaborn 的 regplot 和 FacetGrid 轻松实现这一点。

下面，我们可以看到使用弹性预测进行的分层。请记住，所有这些都是在测试集中完成的。

g = sns.FacetGrid(bands_df, col="elast_band")
g.map_dataframe(sns.regplot, x="price", y="sales")
g.set_titles(col_template="Elast. Band {col_name}");

正如我们所看到的，看起来这种分层方案很有用。对于第一个分层，价格敏感性很高。随着价格的上涨，销售额下降了很多。然而，对于第二个分层，随着价格的上涨，销售大致保持不变。事实上，当我们提高价格时，甚至看起来销量也在上升，但这可能是噪音。

现在与使用 ML 预测模型进行的用户分层进行对比：

g = sns.FacetGrid(bands_df, col="pred_band")
g.map_dataframe(sns.regplot, x="price", y="sales")
g.set_titles(col_template="Pred. Band {col_name}");

我真的很喜欢这个图，因为它传达了一个非常重要的观点。如您所见，预测模型分层在 y 轴上分割个体单元。如第一幅图所示，在第一个分层所对应的日子里，我们没有售出很多冰淇淋，但在第二个分层对应那些日子里，我们确实卖得更多。我觉得这很神奇，因为预测模型正在做它应该做的事情：它预测销售。它可以区分冰淇淋销售量低和高的日子。

唯一的问题是预测在这里并不是特别有用。最终，我们想知道什么时候可以提高价格，什么时候不能。但是，一旦我们查看预测模型分层中线的斜率，我们就会发现它们并没有太大变化。换句话说，由预测模型定义的两个分层对价格上涨的反应大致相同。这并没有让我们深入了解哪些日子可以提高价格，因为看起来价格根本不会影响销售。

关键思想

我们最终正式确定了条件平均干预效果的概念以及它如何对个性化有用。即，如果我们能了解每个单位对一种干预的反应，即如果我们能了解干预效果的异质性，我们就可以根据单位的个体特点给予最好的干预。

我们还将这个目标与预测模型的目标进行了对比。也就是说，我们正在重新考虑估计任务，从预测原始格式的 Y 到预测 Y 如何随 T、 $\frac{\delta y}{\delta t}$ 。

可悲的是，如何为此构建模型并不明显。由于我们不能直接观察弹性，因此很难建立一个预测它的模型。但是线性回归拯救了我们。通过使用适合预测 Y 的回归模型，我们找到了一种方法来预测 $\frac{\delta y}{\delta t}$ 。我们还必须包括干预和特征的交互项。这使得我们对每个客户的弹性预测都不同。换句话说，我们现在正在估计 E[T′(t)|X]。然后使用这些弹性预测将我们的单位分组为或多或少对干预敏感，最终帮助我们确定每组的干预水平。