思路实现

归并排序属于分治算法，分治算法有三个步骤：

1. 分：将问题划分为多个规模较小的子问题，这些子问题与原始问题相似。
2. 治：递归地解决这些子问题。如果子问题足够小，可以直接求解。
3. 合：将子问题的解合并为原始问题的解。

归并排序的重点主要是 合，合 的过程中就会直接排好序。（这里是从小到大排序）

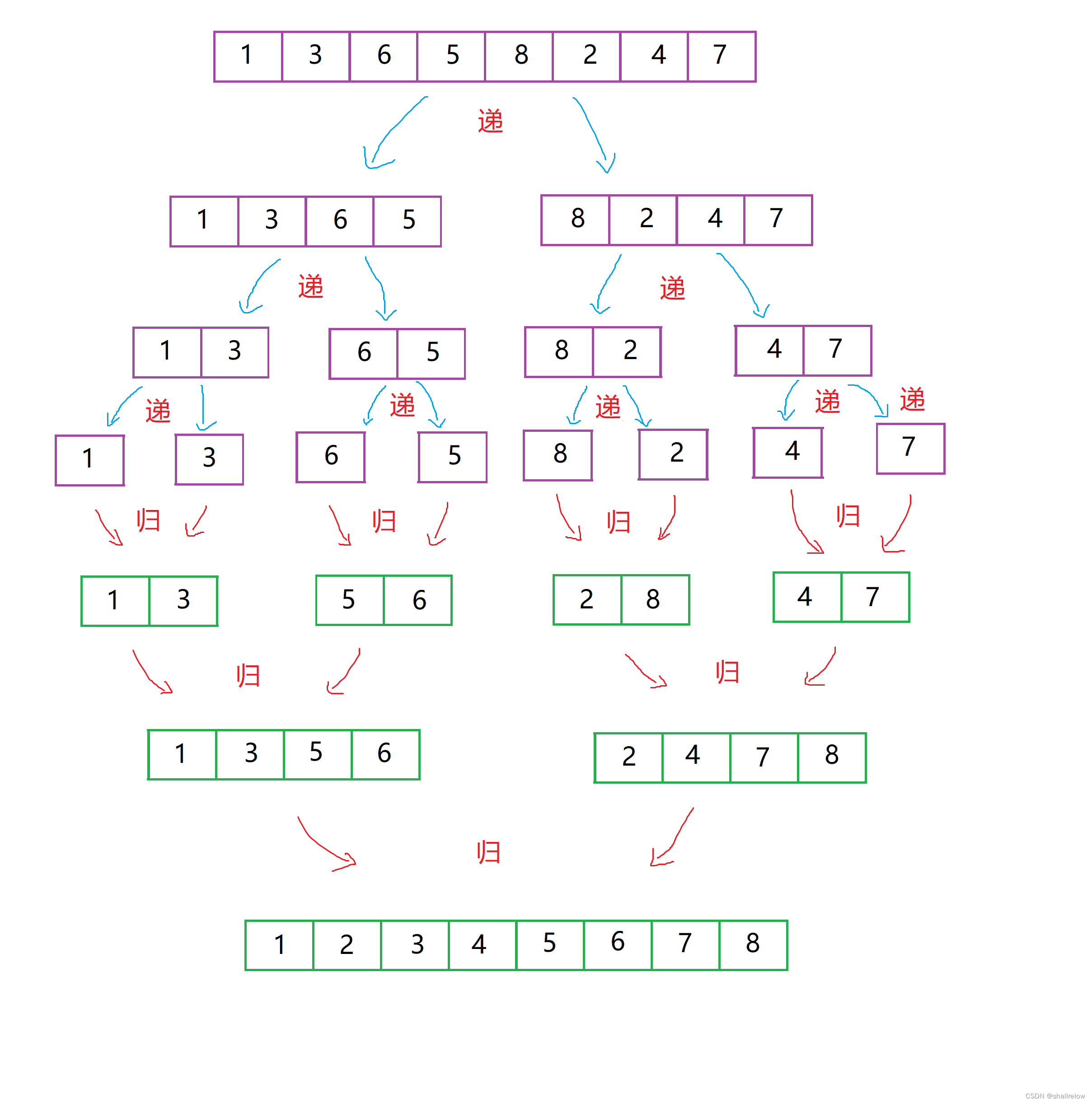
我们来模拟一下合的过程。

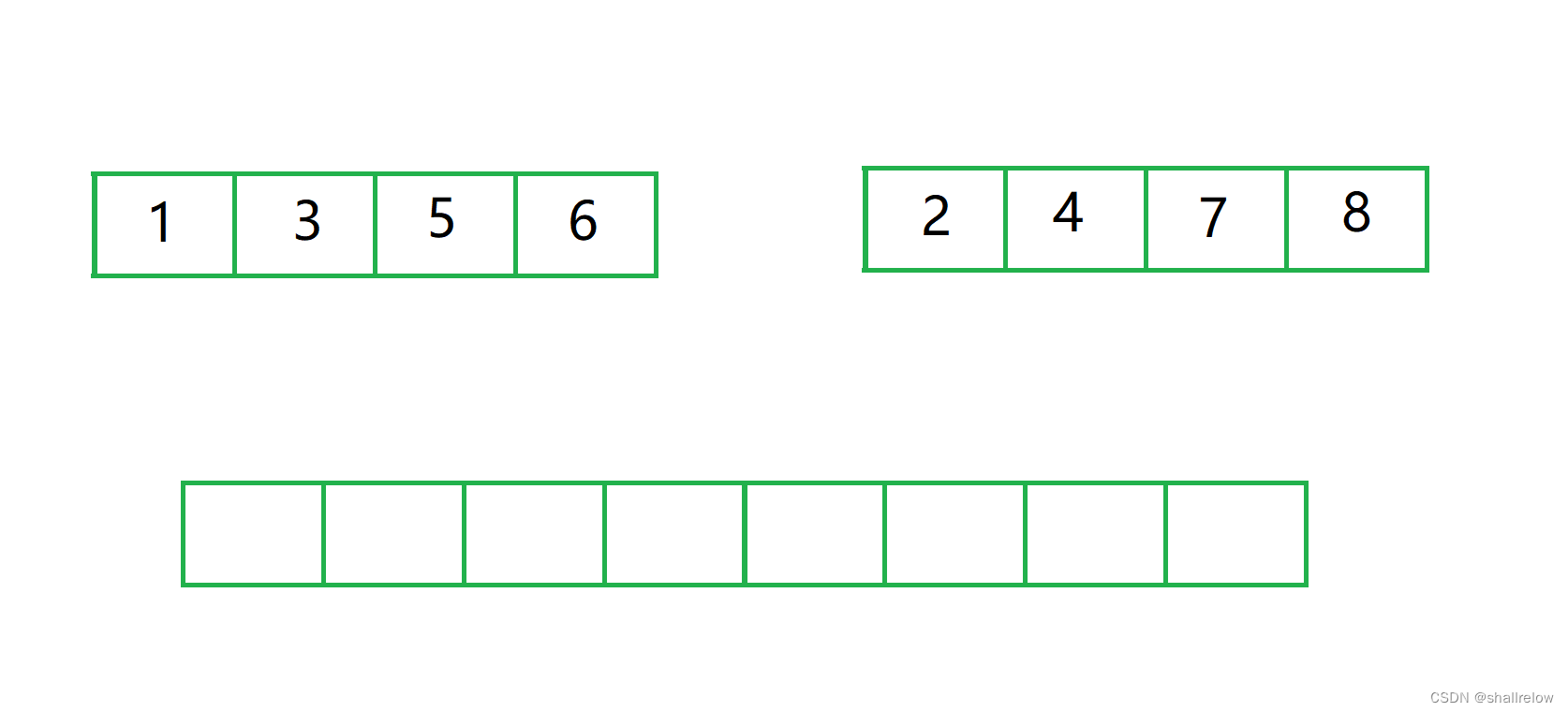
首先合的两个序列，一定都已经是有序的了。（如果不理解这个“一定有序” 后面会说的，先理解怎么合并的）

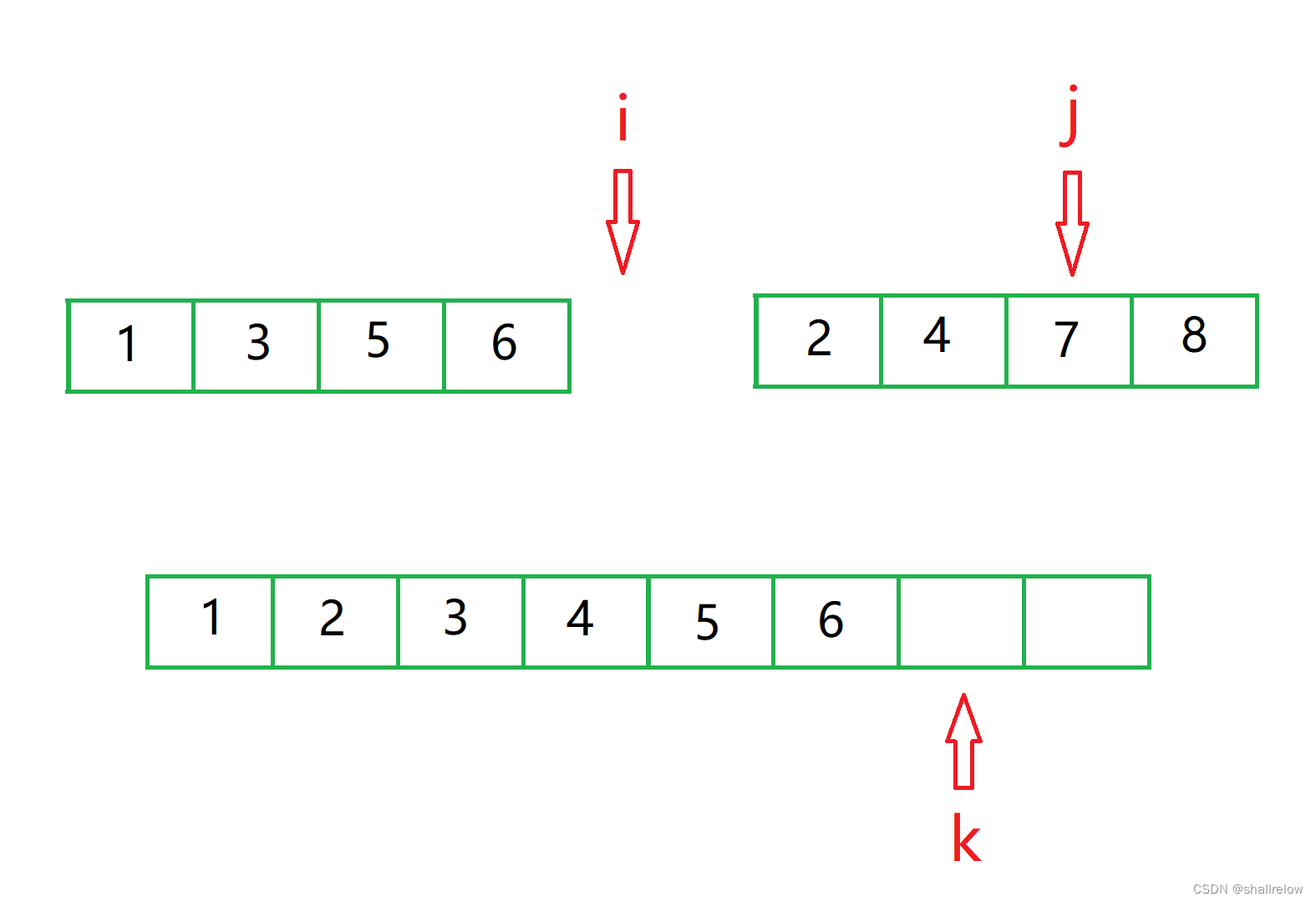
在合的过程中，有一块临时数组，也就是图中这个空的空间。

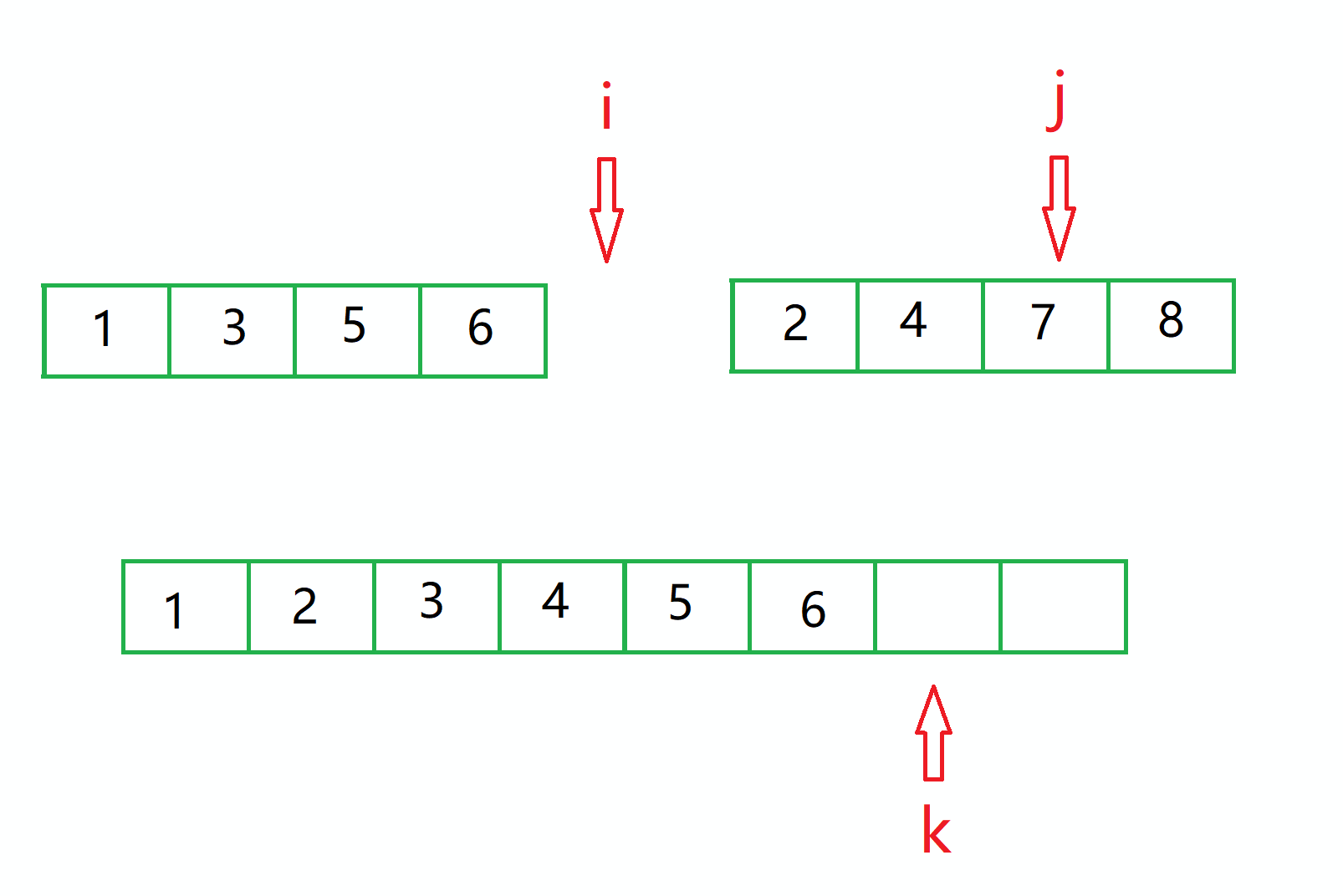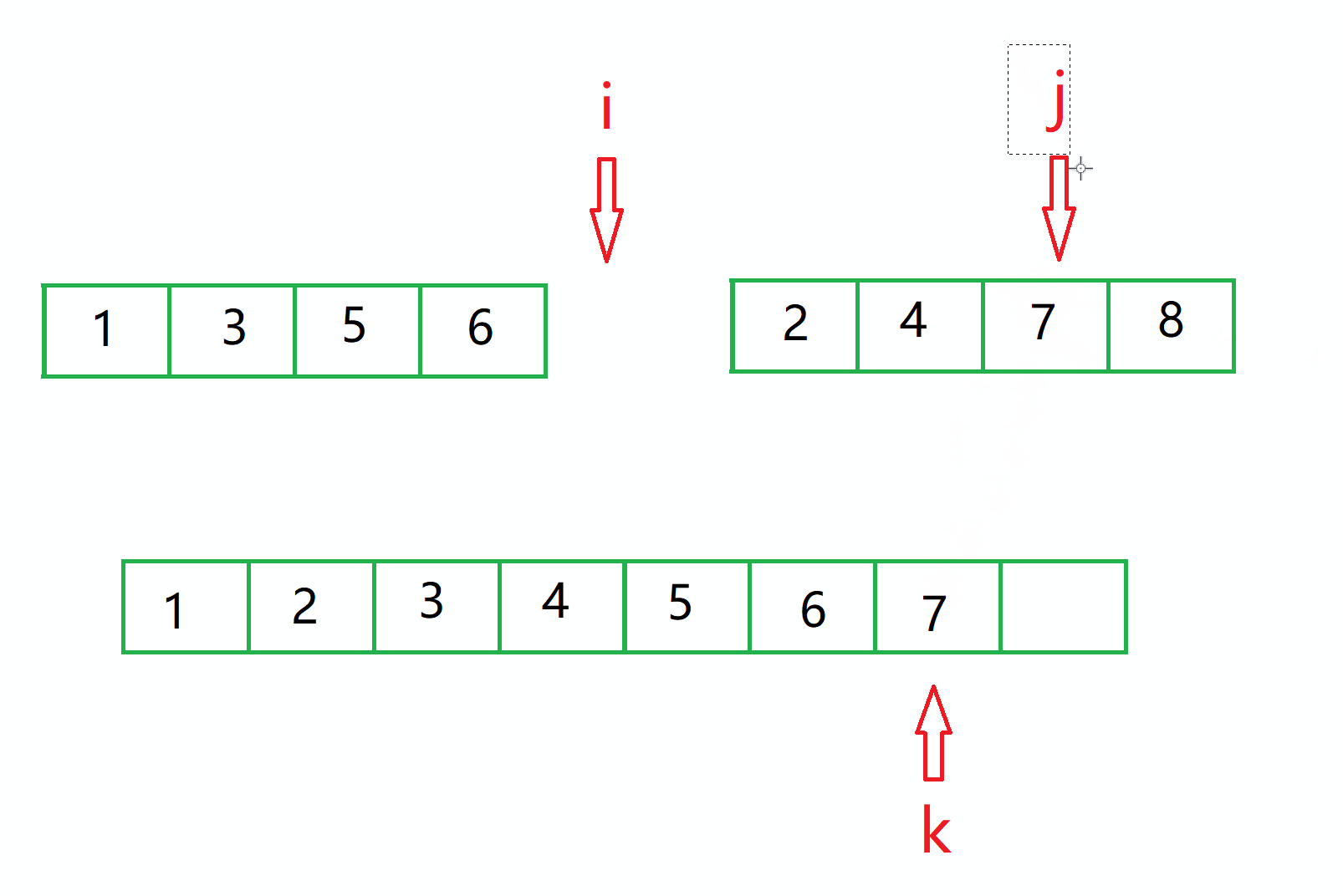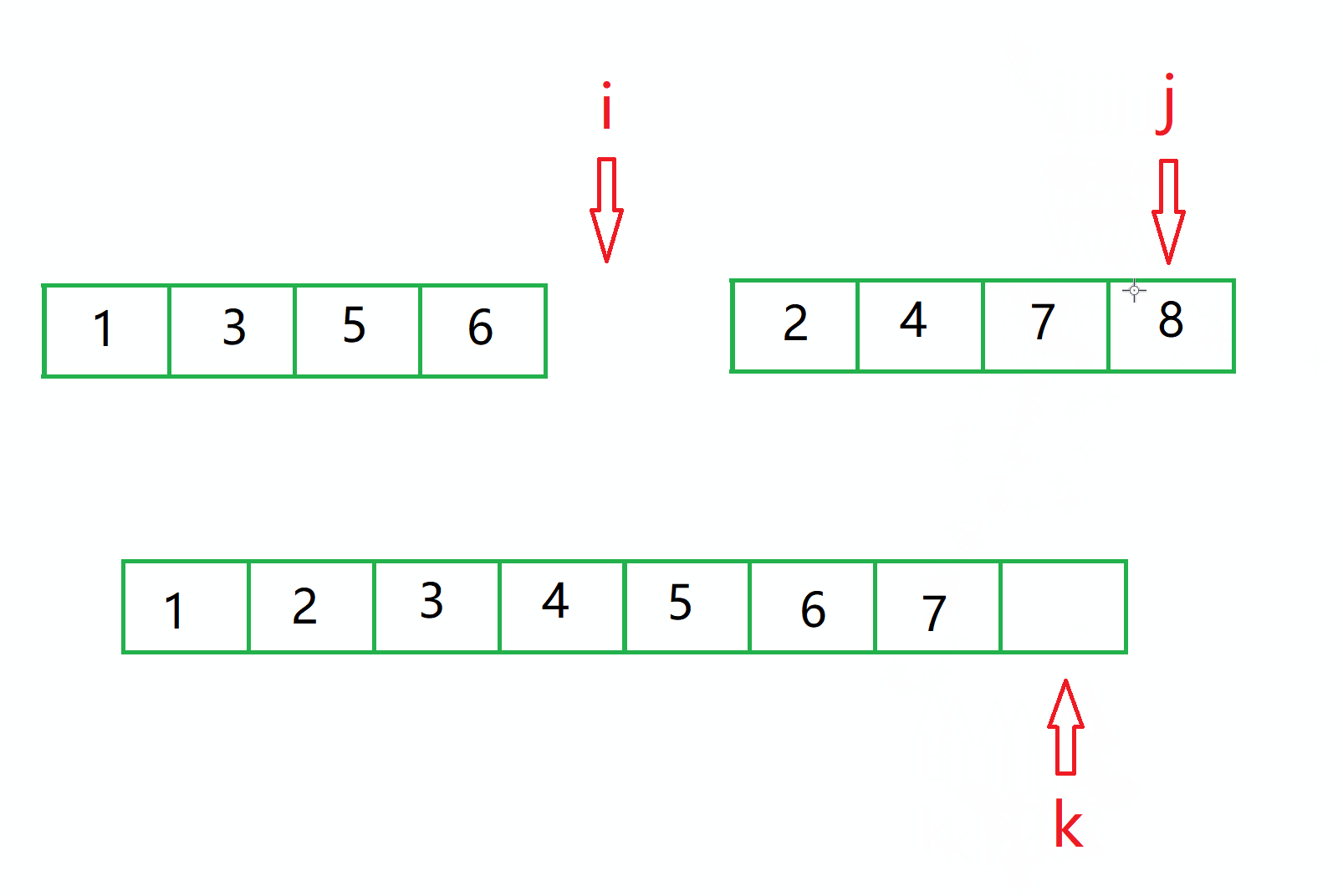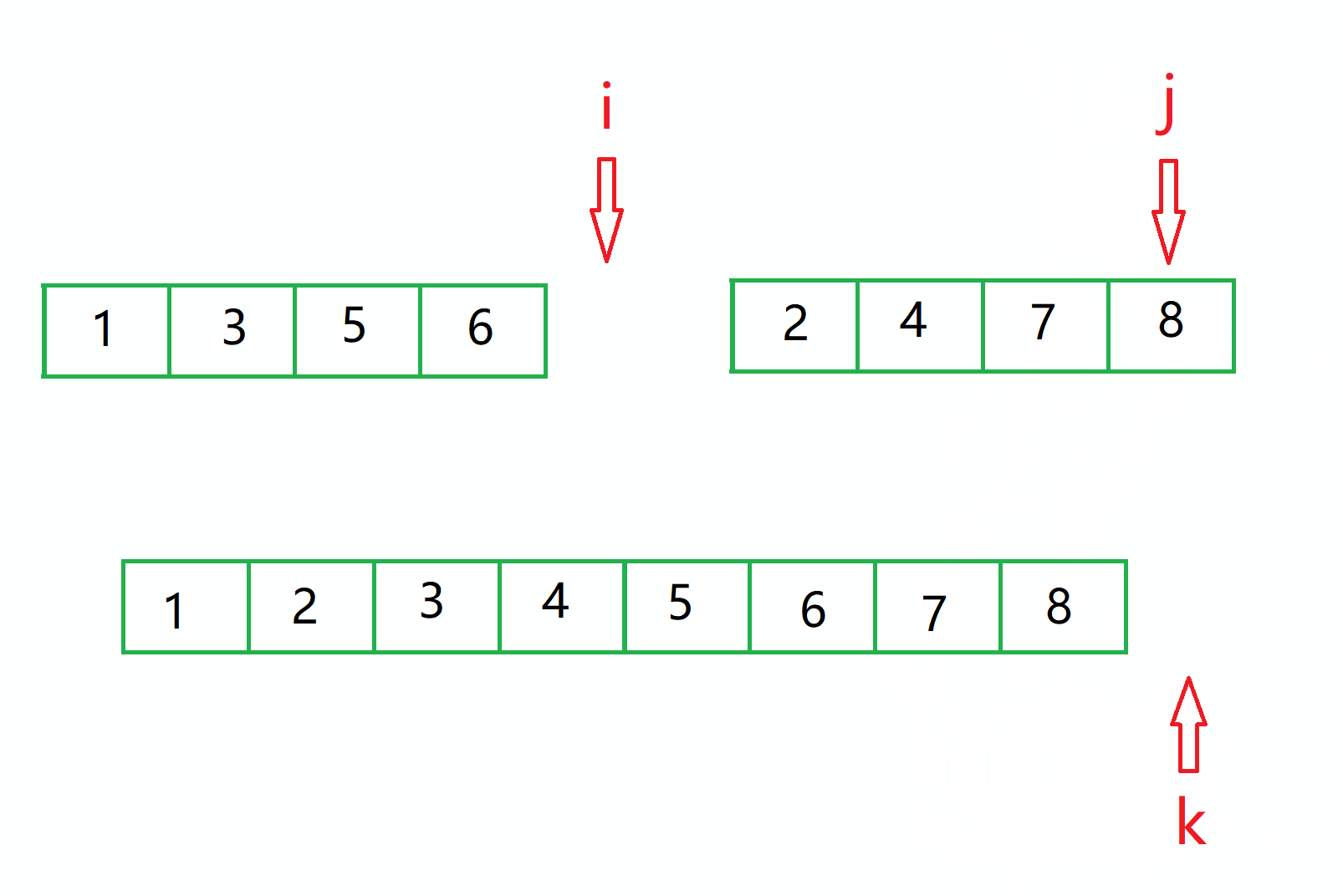
此时需要三个下标，分别指向两个序列的头和 那份空的空间的头。

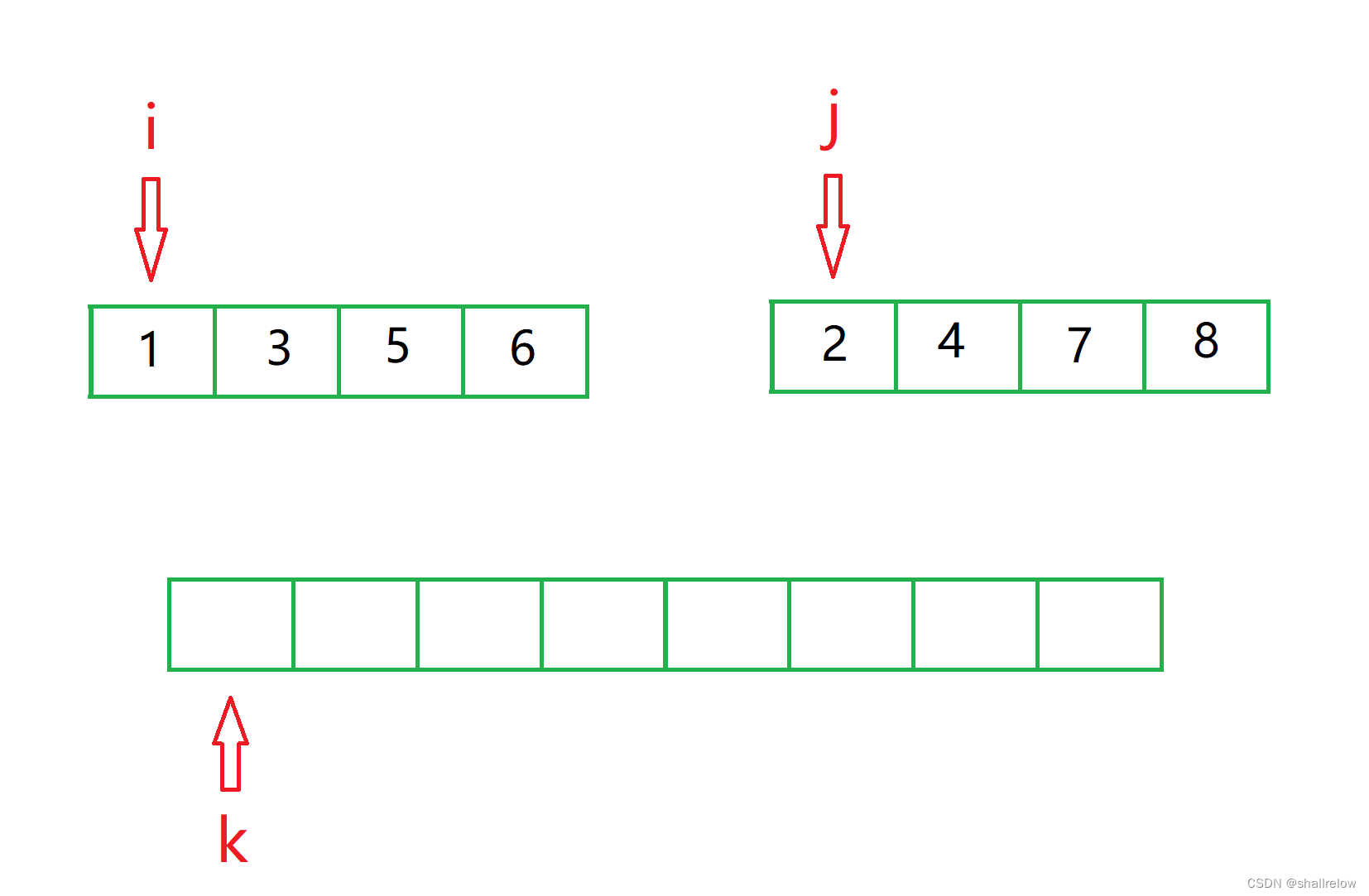
此时比较 下标 i 和 j 的 值，小的那个 赋给 临时空间的 k 坐标，然后 小的坐标 和 k 都自增1。

对于图中的情况，那么就是1 过去。

然后继续比较 下标 为 i 的值和 下标为 j 的值。

此时 j 小，所以 2 过去。

然后一直重复此效果，此时必定有一个序列先把自己的数字 放完了。

比如图中的情况。

最终 下标 i 会移动到序列的外部（当然其实他是指向了右边的那个2，因为这两个序列其实是连续的）

所以此时不能够再次比较了。

接下来我们就需要判断 i 和 j 谁是否在序列内，谁在序列内，就循环的将值放到数组内。

比如这时 只有 j 在序列内部，所以就循环的将值放到临时数组里面，直到 j 出去了。

此时就会发现数组 排序好了。

---

而为什么两个序列一定是有序的是因为 归并排序会使用递归，会先递到只有一个元素。

比如刚才的那个图


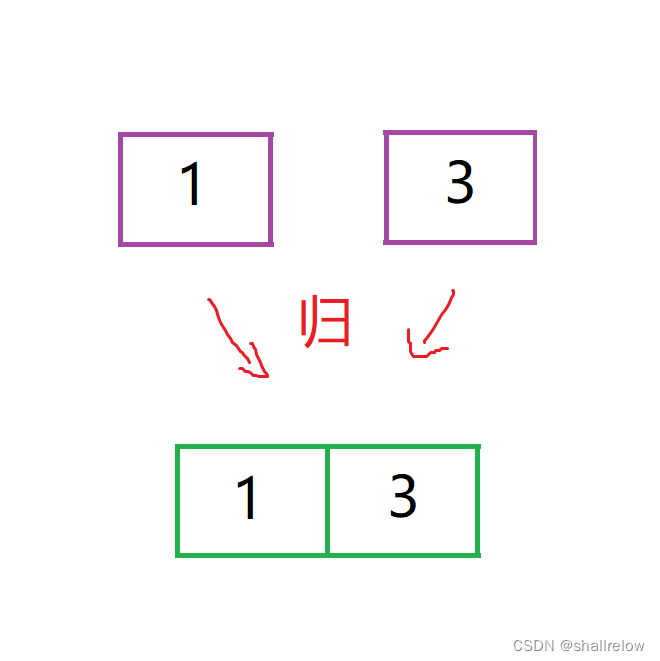
在递到 只有一个元素的时候，它一定是有序的，因为只有一个数字啊。

所以往下合并的时候就一定是 有序的。

代码实现

接下来我们来看看代码，看完代码你就会恍然大悟了，如果没有，那么你可以再次看一下前面的思路。

我们以题目为引入。

题目

给定你一个长度为 $n$ 的整数数列。

请你使用归并排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式

输入共两行，第一行包含整数 $n$。

第二行包含 $n$ 个整数（所有整数均在 $1\sim 10^9$ 范围内），表示整个数列。

输出格式

输出共一行，包含 $n$ 个整数，表示排好序的数列。

数据范围

$1\le n\le 100000$

输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

首先是准备阶段：

其中 题目当中 n 最大为 10的五次方，所以开辟这么大的数组。

这个tem为临时数组。

接着输入环节：

然后把归并排序封装成一个函数，最后直接输出。

对于归并排序函数来说，参数是 要排序的数组 和 要排序的区间头和区间尾。

还记得刚才的分治算法的三个步骤吗？

分、治、合。

首先是分，将问题分为多个子问题。

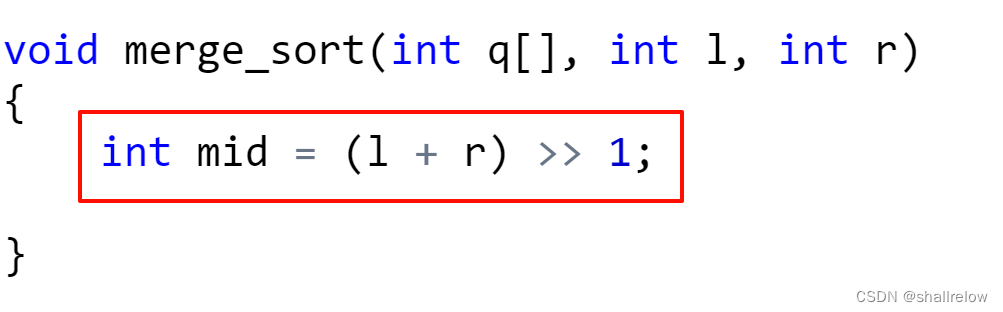
然后是治，递归处理子问题。

一想到递归，你就必须要考虑递归的结束条件，不能说让递归一直递下去。

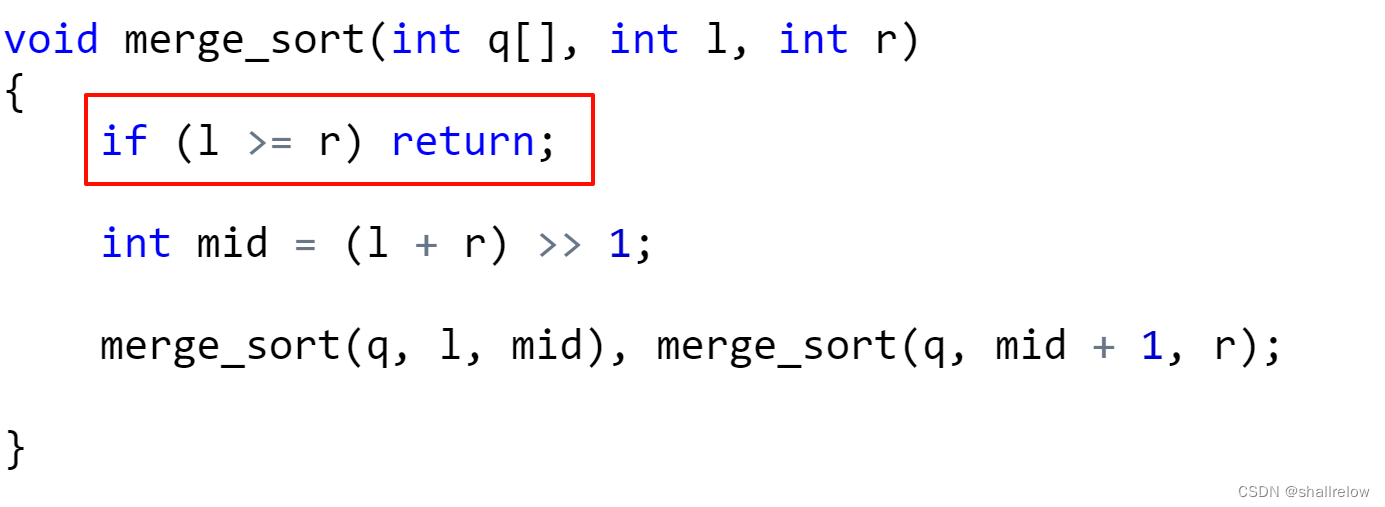
所以我们需要在开头加上此语句。

这句话的意思，如果此时区间内没有元素或只有一个元素，就不需要往下递了。

分 和 治都完了，那么接下来就是 合 了。

还记得刚才的思路吗，首先我们需要创建三个坐标。

其中 下标 i 是 区间 [ l, mid ] 的头，下标 j 是 区间 [ mid+1, r ] 的头，k是 临时数组 tem 的头。

[ l, mid ] 和 [ mid+1, r ] 这两个区间也跟我们上边的递归的区间是一致的。

创建完之后，接下来就是循环比较 i 和 j 的值了。


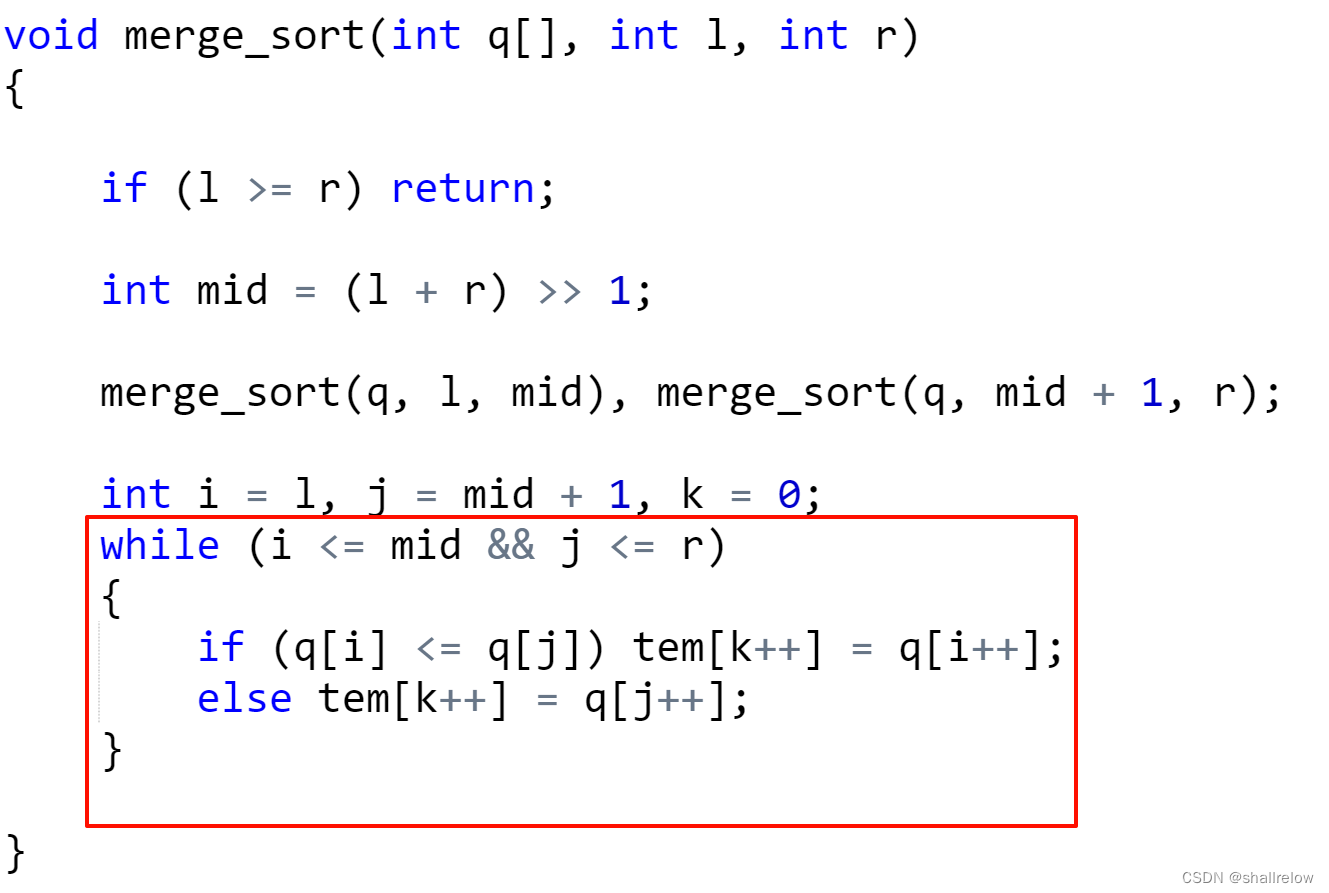
循环直到 i 或者 j 的一个 跳出它的区间 后终止。

接着就需要 让还在 区间内部的 i 或者 j 走完整个区间。

此时临时数组内的值就一定全部有序了，接下来我们需要将这个临时数组的值 搬到我们的原数组中。

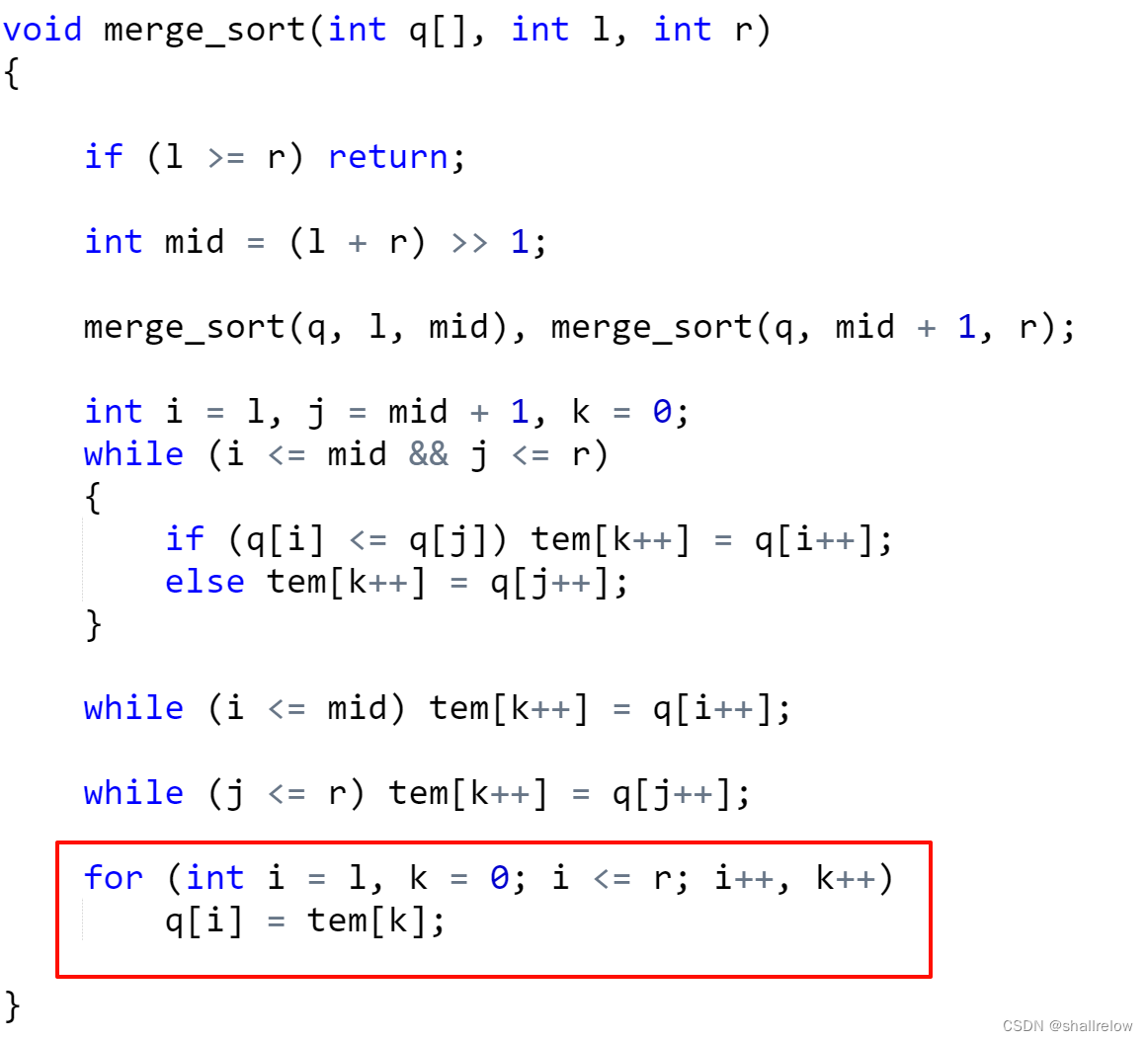
模拟完整过程：


完整代码如下：

#include <iostream>
using namespace std;

const int N = 1e5+10;
int n;
int a[N], tem[N];


void merge_sort(int q[], int l, int r)
{
    
    if (l >= r) return;
    
    int mid = (l + r) >> 1;
    
    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
    
    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r)
    {
        if (q[i] <= q[j]) tem[k++] = q[i++];
        else tem[k++] = q[j++];
    }
    
    while (i <= mid) tem[k++] = q[i++];
    
    while (j <= r) tem[k++] = q[j++];
    
    for (int i = l, k = 0; i <= r; i++, k++)
        q[i] = tem[k];
    
}


int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &a[i]);
    
    merge_sort(a, 0, n-1);
    
    for (int i = 0; i < n; i++) printf("%d ", a[i]);
    return 0;
}

完