1、conv 卷积和多项式乘法
语法
语法1:w = conv(u,v) 返回向量 u 和 v 的卷积。
语法2:w = conv(u,v,shape) 返回如 shape 指定的卷积的分段。
参数
u,v — 输入向量 shape — 卷积的分段 'full' (默认) | 'same' | 'valid'
'full':全卷积 ‘same’:与u大小相同的卷积的中心部分'valid':计算没有补零边缘的卷积部分
2、通过卷积计算多项式乘法
代码及运算
u = [1 0 1 1];
v = [2 7 1];
w = conv(u,v)
w =
2 7 3 9 8 13、 向量卷积
代码及运算
u = [1 1 1 1];
v = [1 1 1 1 0 0 0 1 1];
w = conv(u,v)
w =
列 1 至 11
1 2 3 4 3 2 1 1 2 2 2
列 12
14、 卷积的中心部分
'same'代码及运算
u = [-1 2 1 3 1 -2 0 1 2];
v = [2 4 -1 1 1];
w = conv(u,v,'same')
w =
11 7 14 0 -5 8 7 5 -1'full'代码及运算
u = [-1 2 1 3 1 -2 0 1 2];
v = [2 4 -1 1 1];
w = conv(u,v,'full')
w =
列 1 至 11
-2 0 11 7 14 0 -5 8 7 5 -1
列 12 至 13
3 2'valid'代码及运算
u = [-1 2 1 3 1 -2 0 1 2];
v = [2 4 -1 1 1];
w = conv(u,v,'valid')
w =
14 0 -5 8 75、 conv2 二维卷积
语法
语法1:C = conv2(A,B) 返回矩阵 A 和 B 的二维卷积。
语法2:C = conv2(u,v,A) 首先求 A 的各列与向量 u 的卷积,然后求每行结果与向量 v 的卷积。
语法3:C = conv2(___,shape) 根据 shape 返回卷积的子区。
1)二维卷积
代码及运算
A = rand(3);
B = rand(4);
Cfull = conv2(A,B)%6*6
Csame = conv2(A,B,'same')%中心部位
Cfull =
0.0781 0.8435 1.6181 1.6544 1.5357 0.7213
0.2367 1.2223 2.9144 3.6484 2.8119 1.0920
0.5183 1.4313 3.4028 4.2039 3.0881 1.3723
0.2844 2.0170 2.9532 3.0694 2.6967 0.9839
0.4857 1.3186 1.8013 1.5967 1.3232 0.4820
0.5008 0.1639 0.8645 0.2304 0.3948 0.0831
Csame =
3.4028 4.2039 3.0881
2.9532 3.0694 2.6967
1.8013 1.5967 1.32322)例子:提取二维台座边
代码及运算
A = zeros(10);
A(3:7,3:7) = ones(5);
mesh(A)视图效果

1) 计算水平边
代码及运算
u = [1 0 -1]';
v = [1 2 1];
Ch = conv2(u,v,A);
mesh(Ch)视图效果

2)计算垂直边
代码及运算
Cv = conv2(v,u,A);
mesh(Cv)视图效果
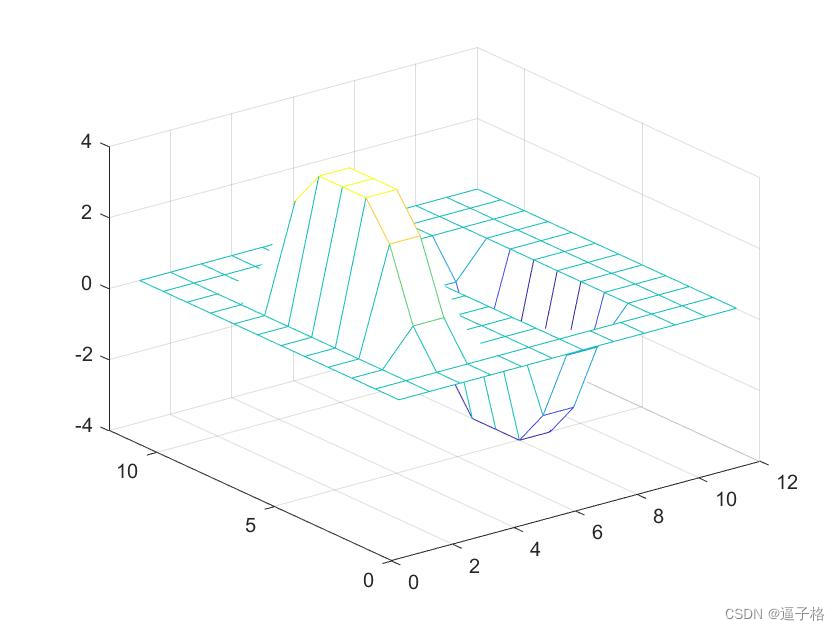
3) 绘制组合边长
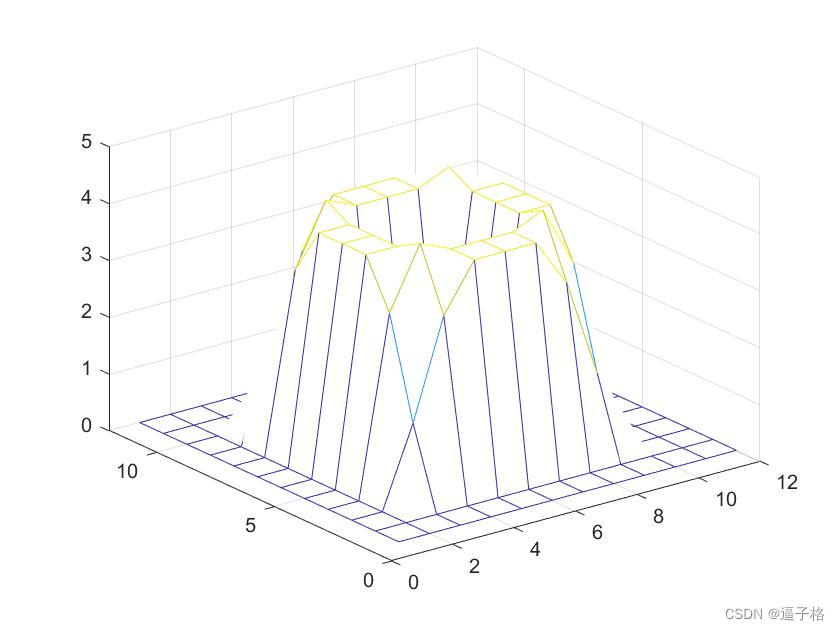
6、convn N 维卷积
语法
语法1:C = convn(A,B) 返回数组 A 和 B 的 N 维卷积。
语法2:C = convn(A,B,shape) 根据 shape 返回卷积的子区。
1)三维卷积
代码及运算
A = rand(2,3,2);
B = 0.25*ones(2,2,2);
C = convn(A,B)
C(:,:,1) =
0.1765 0.2457 0.0935 0.0243
0.1845 0.2652 0.3109 0.2301
0.0080 0.0195 0.2174 0.2059
C(:,:,2) =
0.3502 0.6570 0.4408 0.1340
0.4375 0.7644 0.7622 0.4352
0.0872 0.1074 0.3214 0.3013
C(:,:,3) =
0.1737 0.4113 0.3472 0.1097
0.2530 0.4991 0.4512 0.2051
0.0793 0.0879 0.1040 0.0954代码及运算
A = rand(2,3,2);
B = 0.25*ones(2,2,2);
C = convn(A,B,'same')
C(:,:,1) =
1.1643 0.8855 0.4774
0.6798 0.4946 0.2022
C(:,:,2) =
0.6049 0.4434 0.2044
0.3586 0.2106 0.0407代码及运算
A = rand(2,3,2);
B = 0.25*ones(2,2,2);
C = convn(A,B,'full')
C(:,:,1) =
0.0297 0.2697 0.3863 0.1463
0.1543 0.4794 0.5273 0.2023
0.1246 0.2097 0.1410 0.0560
C(:,:,2) =
0.2176 0.5840 0.7355 0.3690
0.4059 1.0322 1.2911 0.6648
0.1884 0.4482 0.5556 0.2958
C(:,:,3) =
0.1878 0.3143 0.3492 0.2227
0.2516 0.5528 0.7638 0.4625
0.0638 0.2385 0.4146 0.2398代码及运算
A = rand(2,3,2);
B = 0.25*ones(2,2,2);
C = convn(A,B,'valid')
C =
0.8574 0.8072