Plonky3和Binius中的Brakedown多项式承诺协议解析及优化（3）

news2024/11/24 3:10:05

3.2 Expander Graph and Linear-Time Encodable Linear Code

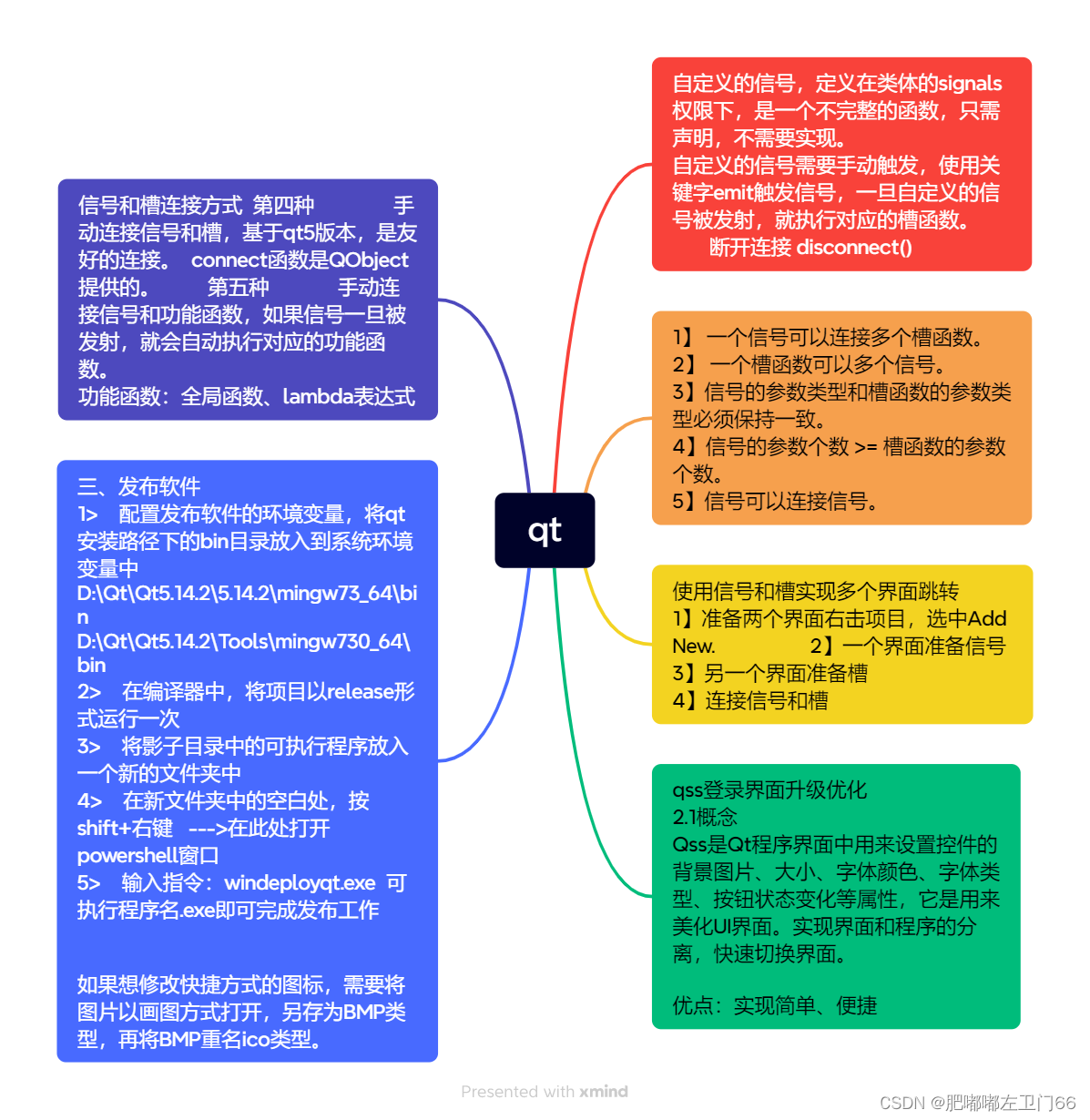
线性时间编码是线性纠错码的一种，核心是扩展图（Expander Graph），如下图所示：

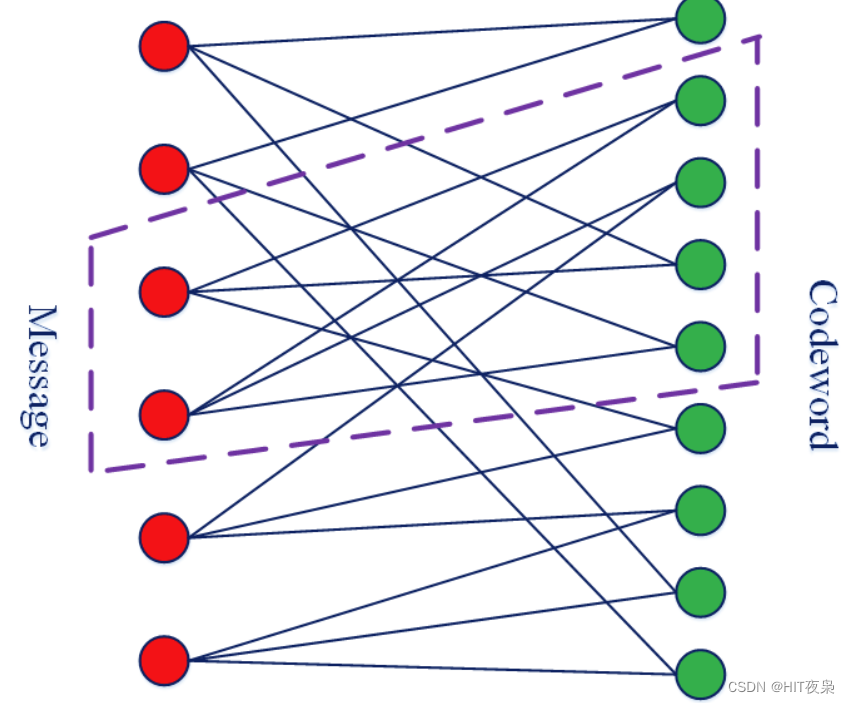
在这里插入图片描述

Figure 3 Expander Graph

Expander Graph是一种具有强连通性的稀疏图，用 $G_{n,m,d}$ 表示，其中 $n$ 为左边Message节点的个数， $m$ 为右边Codeword节点的个数， $d$ 为每个左边顶点链接右边节点的个数，如上图可写为 $G_{6,9,3}$ 。这种编码方式是线性码，可以用一个 $n$ 行 $m$ 列的生成矩阵 $\mathbf{M}_{n,m,d}$ 来表示(矩阵的每一行有 $d$ 个非零元素)，而且这个编码方式可以在线性时间内完成，因为左侧的每个信源符号都与有限 $d$ 个码元符号相关，因此编码的时间为信源符号数量的常数 $d$ 倍。

设置一组参数： $0<\alpha<1$ ， $0<\beta<\frac{\alpha}{1.28}$ ， $r\geq \frac{1+2\beta}{1-\alpha}> 1$ ， $c_n\geq 3$ ， $d_n\geq 3$ ，[5]给出了Expander Graph的线性时间编码过程：

在这里插入图片描述

这里，
$\begin{aligned} c_n=&\Bigg\lceil \min \Big(\max(1.28\beta n,\beta n+4),\\ &\frac{1}{\beta \log_2{\frac{\alpha}{1.28\beta}}}\big( \frac{110}{n}+ H(\beta)+\alpha H(\frac{1.28\beta}{\alpha})\big) \Big)\Bigg\rceil \end{aligned}$

$\begin{aligned} d_n=&\Bigg\lceil \min \Big( \big( 2\beta+\frac{(r-1)+110/n}{\log_2q}\big)n,D\Big)\Bigg\rceil \end{aligned}$

$\begin{aligned} D=\max\Bigg(&\frac{r\alpha H(\beta /r)+\mu H(\nu /\mu)+110/n}{\alpha \beta \log_2{\frac{\mu}{\nu}}},\\ &\frac{r\alpha H(\beta /(r\alpha))+\mu H((2\beta+0.03)/\mu)+110/n}{\beta \log_2{\frac{\mu}{2\beta+0.03}}},\\ &(2\beta+0.03)\Big(\frac{1}{\alpha r-\beta}+\frac{1}{\alpha \beta}+\frac{1}{\mu -2\beta -0.03}\Big)+1 \Bigg) \end{aligned}$

其中， $H(x)=-x\log_2x-(1-x)\log_2(1-x)$ 表示二进制熵函数（binary entropy function）， $\mu =r-1-r\alpha$ , $\nu =\beta +\alpha \beta +0.03$ 。

编码算法是一个递归的过程，目的是构造一个线性映射 $\mathbf{Enc}_n:\mathbf{F}^n\rightarrow\mathbf{F}^{rn}$ ，即对于任意长度为 $n$ 的域向量 $x$ 映射到一个长度为 $r n$ 的域向量 $\omega$ 。码字 $\omega$ 由三部分组成，分别是 $x$ ， $z$ ， $\nu$ (前 $n$ 位与信息相同)，码率为 $1/ r$ ，码字距离为固定值 $\gamma = \beta /r$ 。算法中有两个Expander Graph生成矩阵，分别是 $\mathbf{M}_{n,\alpha n,c_n}$ 和 $\mathbf{M}_{\alpha rn,(r-1-r\alpha)n,d_n}$ 。算法示意图如下。

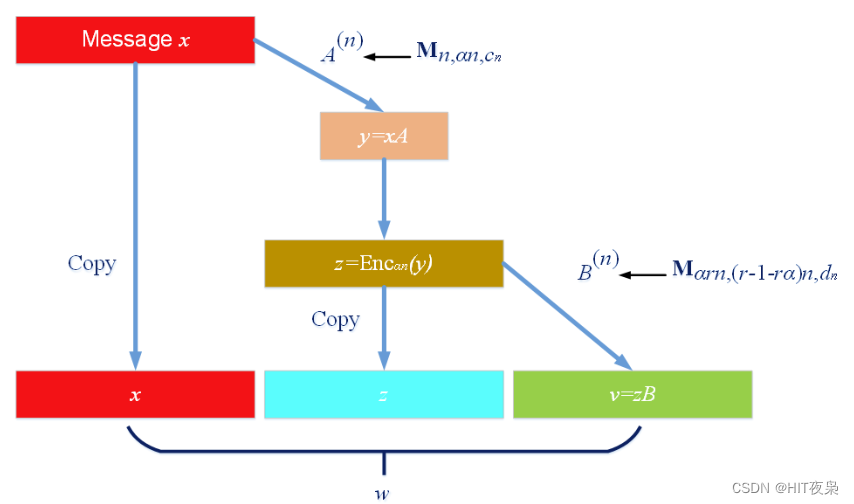
在这里插入图片描述

Figure 4 基于Expander Graph的线性时间编码

线性时间编码是递归进行的，需要设置一个边界条件结束递归进程，在Brakedown中当信息元的长度小于30 的时候就可以终止递归。

Brakedown无需透明设置，承诺和 Prover Time为 $O (d)$ ，与多项式大小呈线性阶，而且很有可能满足后量子安全性，唯一的缺点是证明的大小比较大，达到了 $O (d)$ 。

当然Brakedown是一种成长型承诺方案，既能用于单变量多项式承诺，也可用于multilinear多项式承诺方案中，随着新的哈希函数和新的纠错码的开发，它在未来还有很大的优化空间。

4. Breakdown的优化

由以上分析可知，Breakdown多项式承诺的唯一缺点是证明的大小较大，因此，Breakdown的优化方向是如何减少证明的大小。已有的手段包括：

①Proximity Test和Consistency Test可以并行执行，并且可以使用相同的查询数据进行测试和评估，或者直接省略Proximity Test；
②改变多项式系数的排列方式(Ligero¹¹采用的方法)，即多项式的系数不必排列为方阵，可以根据实际编码方式和查询方式适当调整行列比例。这种优化可以显著减少证明大小。

除了上述优化方向，本文考虑了另外一种优化思路：扩展多项式系数矩阵的维度空间，并使用二维张量积来表示多项式取值（待开发）。

References：

[1]https://drops.dagstuhl.de/storage/00lipics/lipics-vol107-icalp2018/LIPIcs.ICALP.2018.14/LIPIcs.ICALP.2018.14.pdf

[2] Kate, A., Zaverucha, G.M., Goldberg, I.. Constant-Size Commitments to Polynomials and Their Applications. International Conference on the Theory and Application of Cryptology and Information Security, 2010.

[3] https://doc-internal.dalek.rs/bulletproofs/notes/inner_product_proof/i ndex.html

[4] Ulrich Haböck. A summary on the fri low degree test. Cryptology ePrint Archive, Paper 2022/1216, 2022.

[5] https://eprint.iacr.org/2021/1043.pdf?ref=hackernoon.com

[6] J. Bootle, A. Chiesa, and J. Groth. Linear-time arguments with sub-linear verification from tensor codes. In TCC, 2020.

[7] S. Setty. Spartan: Efficient and general-purpose zkSNARKs without trusted setup. In CRYPTO, 2020.

[8] T. Xie, Y. Zhang, and D. Song, “Orion: Zero knowledge proof with linear prover time,” Cryptology ePrint Archive, Paper 2022/1010, 2022, https://eprint.iacr.org/2022/1010.

[9] B. Diamond, J. Posen,“Succinct Arguments over Towers of Binary Fields,” Cryptology ePrint Archive, Paper 2023/1784, 2023, https://eprint.iacr.org/2023/1784.pdf

[10] https://github.com/IrreducibleOSS/binius

[11] S. Ames, C. Hazay, Y. Ishai, and M. Venkitasubramaniam. Ligero: Lightweight sublinear arguments without a trusted setup. In CCS, 2017

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1831967.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！