应用场景

要求出每两点之间的最短路。或判断两点之间的连通性（两点之间是否有路径）。

板子

代码（必背!!!）

for(int k = 1; k <= n; k++)
  for(int i = 1; i <= n; i++)
    for(int j = 1; j <= n; j++)
      d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
           // 是直接到下一个的边权小， 还是i -> k -> j小

原理（先背代码再理解）

你理解了要被代码， 不理解也要被代码， 背代码只是为了理解好， 所以先背代码再理解！

——老师口头禅

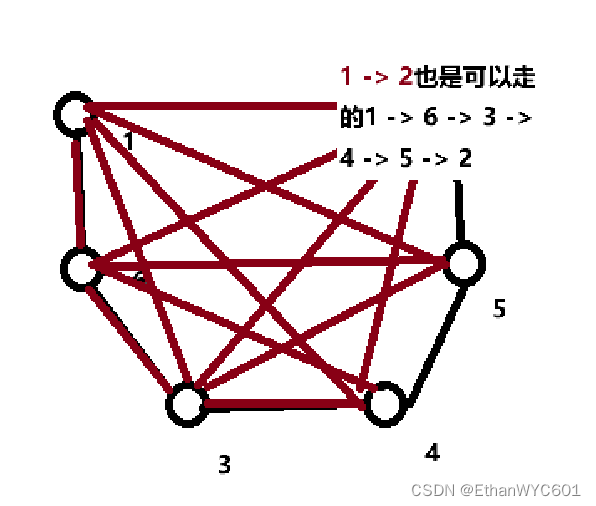
我们来理解一下（画图）：

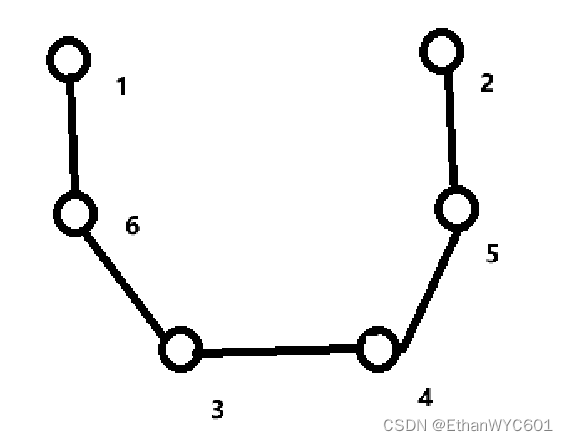
这是一个连通图吧， 我把顺序打乱了，我们来看一下代码会发生什么。

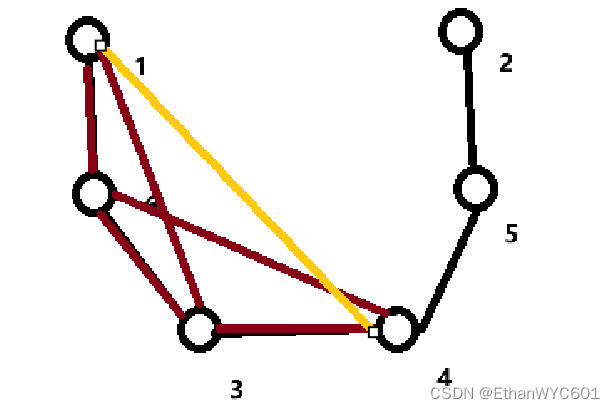
这里的黄线就是以前已经把3连上而1这时从4就可以打达3。

最后我们就可以得到：

转递闭包

  _all(k, 1, N) _all(i, 1, N) _all(j, 1, N) {
    F[i][j] = F[i][j] || (F[i][k] && F[k][j]);
  }