堆
- 堆是一个完全二叉树
- 完全二叉树的要求,除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列
- 堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值
- 堆中每个节点的值都大于等于(或者小于等于)其左右子节点的值
最大堆
- 结点的键值小于等于其父结点的键值

最小堆
- 结点的键值大于等于其父结点的键值

已知父结点
- 一
- 左孩子结点: 2 * 父结点 + 1
- 右孩子结点: 2 * 父结点 + 2
- 二
- 左孩子结点: 2 * 父结点
- 右孩子结点: 2 * 父结点 + 1
已知孩子结点
- 一
- 父结点: 孩子结点 - 1 / 2
- 二
- 父结点: 孩子结点 / 2
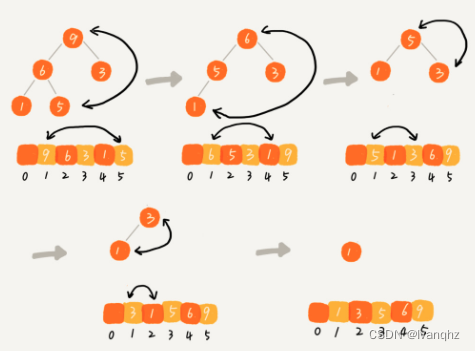
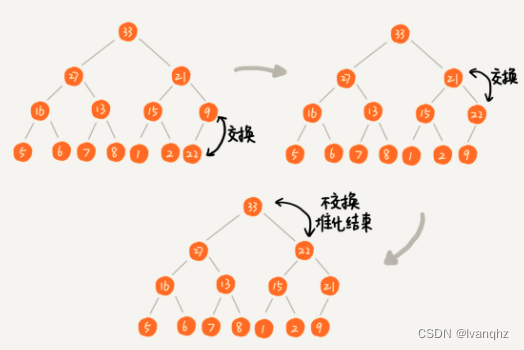
堆化(heapify)
- 堆化实际上有两种,
从下往上和从上往下从下往上-

-
就是顺着节点所在的路径,向上或者向下,对比,然后交换
-
-
让新插入的节点与父节点对比大小。如果不满足子节点小于等于父节点的大小关系,就互换两个节点
-
一直重复这个过程,直到父子节点之间满足刚说的哪种大小关系
-
从上往下-
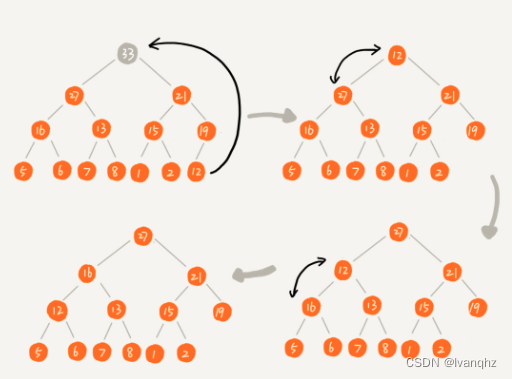
-
把最后一个节点放到堆顶,然后利用同样的父子节点对比的方法
-
对于不满足父子节点大小关系的,互换两个节点,并且重复进行这个过程,直到父子节点之间满足大小关系为止
-
- 时间复杂度
- 一个包含n个节点的完全二叉树,树的高度不会超过log2n
- 堆化的过程是顺着节点所在路径比较的,所以堆化的时间复杂度跟树的高度成正比,也就是O(logn)
- 插入数据和删除堆顶元素的主要逻辑是堆化,所以,往堆中插入一个元素和删除堆顶元素的时间复杂度都是O(logn)
如何基于堆实现排序
- 时间复杂度: O(nlogn)
- 建堆
-
堆排序是原地排序,不借助另一个数组,就在原数组上操作
-
第一种,在堆中插入一个元素的思路
- 通过
从下往上的插入方式,把n个数据插入数组中,形成堆
- 通过
-
第二种,与第一种相反
-
是从后往前处理数组,并且每个数据都是
从上往下堆化 -
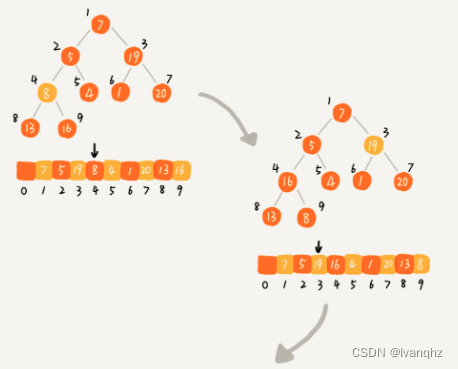
-
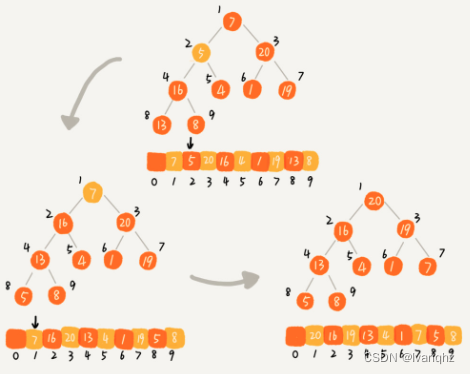
-
-
代码实现
-

-
这段代码里,从下标 n / 2 开始到1的数据进行堆化
-
下标 n / 2 +1 到 n 的节点是叶子节点,不需要堆化
-
从上图代码中,可以看出每个节点的堆化时间复杂度: O(logn)
-
-
时间复杂度
-
每个节点堆化的时间复杂度是O(logn), 那么 n / 2 + 1的总时间复杂度是 O(nlogn)?
-
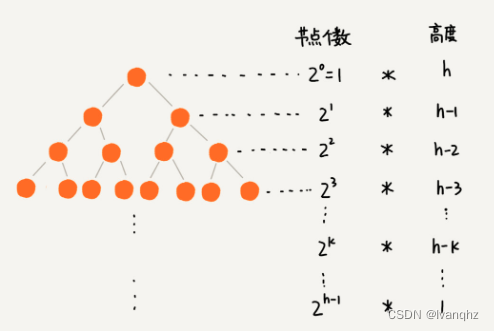
-
求和公式
-

-
求解
-
把公式左右都乘以2,得S2, 然后 S2 - S1 = S
-

-
求解等比数列
-
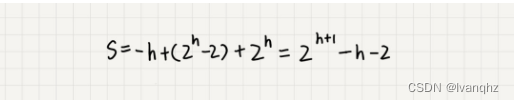
-
因为 h = log2n ,代入公式S,得到S = O(n)
-
-
解答过程
-
-
所以,建堆时间复杂度为:O(n)
-
-
- 排序
-

-
时间复杂度
- 整个堆排序的过程,都只需要极个别临时存储空间,所以堆排序是原地排序算法
- 堆排序包括建堆和排序两个操作,建堆过程的时间复杂度是 O(n),排序过程的时间复杂度是 O(nlogn),所以,堆排序整体的时间复杂度是 O(nlogn)
- 堆排序不是稳定的排序算法,因为在排序的过程,存在将堆的最后一个节点跟堆顶节点互换的操作,所以就有可能改变值相同数据的原始相对顺序
-
为什么快速排序比堆排序性能更好?
- 堆排序数据访问的方式没有快速访问友好
- 对于快速排序来说,数据是顺序访问的。而对于堆排序来说,数据是跳着访问的
- 比如数据的堆化
-

-
对堆顶节点进行堆化,会依次访问数组下标为1,2,4,8的元素,而不是像快速排序那样,局部顺序访问,所以,这样对CPU缓存是很不友好的
-
- 比如数据的堆化
- 对于同样的数据,在排序过程中,堆排序算法数据交换次数要多于快速排序
- 在讲排序的时候,提过两个概念,有序度和逆序度
- 对于基于比较的排序算法来说,整个排序过程就是由两个基本的操作组成的,比较和交换(或移动)
- 快速排序
- 快速排序数据交换的次数不会比逆序度多
- 堆排序
-
堆排序的第一步是建堆,建堆的过程会打乱数据原有的相对先后顺序,导致原数据有序度降低
-
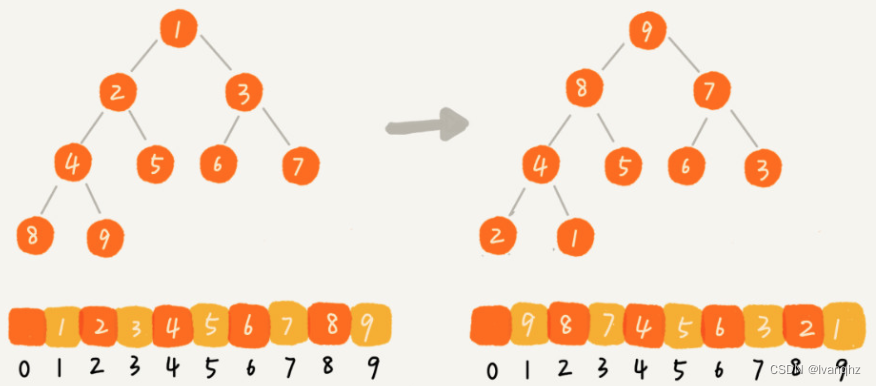
-
对于一组已经有序的数据来说,经过建堆之后,数据反而变得更加无序了
-
- 对于快速排序来说,数据是顺序访问的。而对于堆排序来说,数据是跳着访问的