当数据的维度很高时,很多机器学习问题变得相当困难,这种现象被称为维度灾难(curse of dimensionality)。
在很多实际的问题中,虽然训练数据是高维的,但是与学习任务相关也许仅仅是其中的一个低维子空间,也称为一个低维嵌入,例如:数据属性中存在噪声属性、相似属性或冗余属性等,对高维数据进行降维(dimension reduction)能在一定程度上达到提炼低维优质属性或降噪的效果。
常见的降维方法除了特征选择以外,还有维度变换,即将原始的高维特征空间映射到低维子空间(subspace),并尽量保证数据信息的完整性。常见的维度变换方法有
- 主成分分析:(PCA)是一种无监督的降维方法,其目标通常是减少冗余信息和噪声。
- 因子分析:(FA)是找到当前特征向量的公因子,用公因子的线性组合来描述当前的特征向量。
- 线性判别分析:(LDA)本身也是一个分类模型,是为了让映射后的样本有最好的分类性能。
- 流行学习:(manifold learning)复杂的非线性方法。
主成分分析
主成分分析(Principal Component Analysis,PCA)是一种最常用的数据降维方法,这一方法利用一个正交变换,将原始空间中的样本投影到新的低维空间中。简单来说就是,PCA采用一组新的基来表示样本点,其中每一个基向量都是原来基向量的线性组合,通过使用尽可能少的新基向量来表出样本,从而达到降维的目的。

方差最大化
以往矩阵的样本矩阵 X X X 中,我们用一行表示一个样本点 。由于向量通常是指列向量,所以在PCA相关的文献中,常常用 X X X的每一列来表示一个样本,即给定样本矩阵
X
=
(
x
1
x
2
⋯
x
N
)
=
(
x
11
x
12
⋯
x
1
N
x
21
x
22
⋯
x
2
N
⋮
⋮
⋱
⋮
x
p
1
x
p
2
⋯
x
p
N
)
X=\begin{pmatrix}\mathbf x_1&\mathbf x_2&\cdots&\mathbf x_N\end{pmatrix}= \begin{pmatrix} x_{11}&x_{12}&\cdots&x_{1N} \\ x_{21}&x_{22}&\cdots&x_{2N} \\ \vdots&\vdots&\ddots&\vdots \\ x_{p1}&x_{p2}&\cdots&x_{pN} \\ \end{pmatrix}
X=(x1x2⋯xN)=
x11x21⋮xp1x12x22⋮xp2⋯⋯⋱⋯x1Nx2N⋮xpN
包含
N
N
N 个样本,
p
p
p 个特征。其中,第
j
j
j 个样本的特征向量为
x
j
=
(
x
1
j
,
x
2
j
,
⋯
,
x
p
j
)
T
\mathbf x_j=(x_{1j},x_{2j},\cdots,x_{pj})^T
xj=(x1j,x2j,⋯,xpj)T 。
假定投影变换后得到的新坐标系变换矩阵为
W
p
×
p
=
(
w
1
⋯
w
p
)
W_{p\times p}=\begin{pmatrix}\mathbf w_1&\cdots&\mathbf w_{p}\end{pmatrix}
Wp×p=(w1⋯wp)
其中
w
j
\mathbf w_j
wj 是标准正交基向量,即
∥
w
j
∥
2
=
1
,
w
i
T
w
j
=
0
(
i
≠
j
)
\|\mathbf w_j\|_2=1,\ \mathbf w_i^T\mathbf w_j=0(i\neq j)
∥wj∥2=1, wiTwj=0(i=j) 。样本点
x
j
\mathbf x_j
xj 在新坐标系中的样本
z
j
=
W
T
x
j
\mathbf z_j=W^T\mathbf x_j
zj=WTxj
正交变换后得到的样本矩阵
Z
=
W
T
X
Z=W^T X
Z=WTX
若要用一个超平面对空间中所有高维样本进行恰当的表达,那么它大概应具有这样的性质:
- 最近重构性:样本点到超平面的距离足够近,即尽可能在超平面附近;
- 最大可分性:样本点在超平面上的投影尽可能地分散开来,即投影后的坐标具有区分性。
有趣的是,最近重构性与最大可分性虽然从不同的角度出发,但最终得到了完全相同的优化函数。
在此,我们从最大可分性出发推导,样本在新空间每维特征上尽可能的分散,因此要求 Z Z Z 各行方差最大化。
新空间第
i
i
i 行的特征向量
z
i
=
(
z
i
1
,
⋯
,
z
i
p
)
\mathbf z_i=(z_{i1},\cdots,z_{ip})
zi=(zi1,⋯,zip) ,各行方差之和
1
N
∑
i
=
1
p
(
z
i
−
z
ˉ
i
)
(
z
i
−
z
ˉ
i
)
T
=
1
N
tr
(
Z
−
z
ˉ
)
(
Z
−
z
ˉ
)
T
\frac{1}{N}\sum_{i=1}^p(\mathbf z_i-\bar z_i)(\mathbf z_i-\bar z_i)^T =\frac{1}{N}\text{tr }(Z-\bar{\mathbf z})(Z-\bar{\mathbf z})^T
N1i=1∑p(zi−zˉi)(zi−zˉi)T=N1tr (Z−zˉ)(Z−zˉ)T
新空间各特征的样本均值
z
ˉ
=
1
N
∑
j
=
1
N
z
j
=
W
T
x
ˉ
\bar{\mathbf z}=\frac{1}{N}\sum_{j=1}^N\mathbf z_j=\mathbf W^T\bar{\mathbf x}
zˉ=N1j=1∑Nzj=WTxˉ
其中
x
ˉ
\bar{\mathbf x}
xˉ 是原空间各特征的样本均值
x
ˉ
=
1
N
∑
j
=
1
N
x
j
\bar{\mathbf x}=\frac{1}{N}\sum_{j=1}^N\mathbf x_j
xˉ=N1j=1∑Nxj
为方便求解,主成分分析中,首先对给定数据进行了中心化,即
Σ
j
x
j
=
0
\Sigma_j\mathbf x_j=0
Σjxj=0,所以新空间中各特征的样本均值
z
ˉ
=
0
\bar{\mathbf z}=0
zˉ=0。于是,转换后各行方差之和简化为
1
N
tr
(
Z
Z
T
)
=
1
N
tr
(
W
T
X
X
T
W
)
\frac{1}{N}\text{tr}(ZZ^T)=\frac{1}{N}\text{tr}(W^TXX^TW)
N1tr(ZZT)=N1tr(WTXXTW)
从最大可分性出发,应该使投影后样本点的方差最大化。同时
w
i
\mathbf w_i
wi 是标准正交基,从而保证了转换后的特征相互独立,且系数唯一。于是优化目标可写为
max
W
tr
(
W
T
X
X
T
W
)
s.t.
W
T
W
=
I
\max_W\text{tr}(W^TXX^TW) \\ \text{s.t.}\quad W^TW=I
Wmaxtr(WTXXTW)s.t.WTW=I
特征值分解
接着使用拉格朗日乘子法求解上面的优化问题,得到
X
X
T
W
=
W
Λ
XX^TW=W\Lambda
XXTW=WΛ
其中拉格朗日乘子
Λ
=
diag
(
λ
1
,
⋯
,
λ
p
)
\Lambda=\text{diag}(\lambda_1,\cdots,\lambda_p)
Λ=diag(λ1,⋯,λp)。上式可拆解为
X
X
T
w
i
=
λ
i
w
i
(
i
=
1
,
2
,
⋯
,
p
)
XX^T\mathbf w_i=\lambda_i\mathbf w_i\quad (i=1,2,\cdots,p)
XXTwi=λiwi(i=1,2,⋯,p)
从上式可知,
w
i
\mathbf w_i
wi 是协方差矩阵
X
X
T
XX^T
XXT 的特征向量,
λ
i
\lambda_i
λi 为特征值。因此,主成分分析可以转换成一个矩阵特征值分解问题。我们的目标函数可变为
tr
(
W
T
X
X
T
W
)
=
tr
(
W
T
W
Λ
)
=
tr
(
Λ
)
=
∑
i
=
1
p
λ
i
\text{tr}(W^TXX^TW)=\text{tr}(W^TW\Lambda)=\text{tr}(\Lambda)=\sum_{i=1}^p\lambda_i
tr(WTXXTW)=tr(WTWΛ)=tr(Λ)=i=1∑pλi
可知,特征值
λ
\lambda
λ 是投影后样本的方差。于是,要取得降维后的方差最大值,只需对协方差矩阵
X
X
T
XX^T
XXT 进行特征值分解,将求得的特征值排序:
λ
1
⩾
⋯
⩾
λ
p
\lambda_1\geqslant\cdots\geqslant\lambda_p
λ1⩾⋯⩾λp ,再取前
p
′
p'
p′ 个特征值对应的特征向量构成变换矩阵
W
=
(
w
1
⋯
w
p
′
)
W=\begin{pmatrix}\mathbf w_1&\cdots&\mathbf w_{p'}\end{pmatrix}
W=(w1⋯wp′)
于是,可得到的变换后的样本矩阵
Z
=
W
T
X
Z=W^T X
Z=WTX
这些变换后线性无关的特征称为主成分(Principal Components)。
实践中常通过对 X X X 进行奇异值分解来代替协方差矩阵的特征值分解。
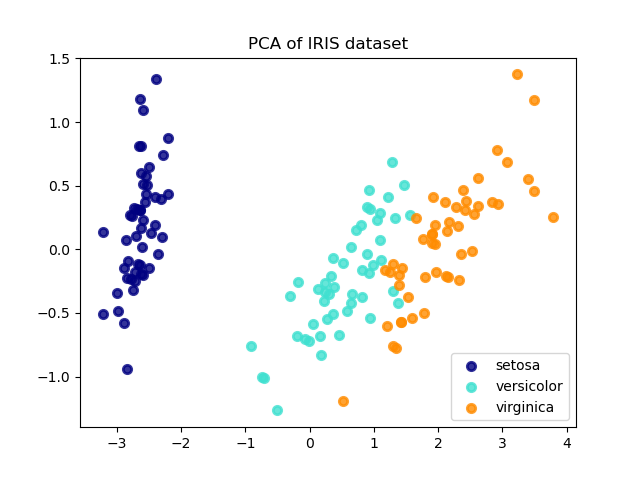
主成分维数的选择
降维后低维空间的维数
p
′
p'
p′ 通常是由用户事先指定,或通过在
p
′
p'
p′ 值不同的低维空间中对 k 近邻分类器(或其他开销较小的学习器)进行交叉验证来选取较好的
p
′
p'
p′值。对 PCA,还可从重构的角度设置一个重构阈值,例如
t
=
95
%
t= 95\%
t=95%, 然后选取使下式成立的最小
p
′
p'
p′ 值:
∑
i
=
1
p
′
λ
i
∑
i
=
1
p
λ
i
⩾
t
\frac{\sum_{i=1}^{p'}\lambda_i}{\sum_{i=1}^p\lambda_i}\geqslant t
∑i=1pλi∑i=1p′λi⩾t
主成分分析是一种无监督学习方法,可以作为监督学习的数据预处理方法,用来去除噪声并减少特征之间的相关性,但是它并不能保证投影后数据的类别。
优缺点总结
PCA算法的主要优点有:
- 仅仅需要以方差衡量信息量,不受数据集以外的因素影响。
- 各主成分之间正交,可消除原始数据成分间的相互影响的因素。
- 计算方法简单,主要运算是特征值分解,易于实现。
PCA算法的主要缺点有:
- 主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。
- 方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。
KernelPCA
高维映射
在前面的讨论中,从高维空间到低维空间的函数映射是线性的,然而,在不少现实任务中,我们的样本数据点不是线性分布。
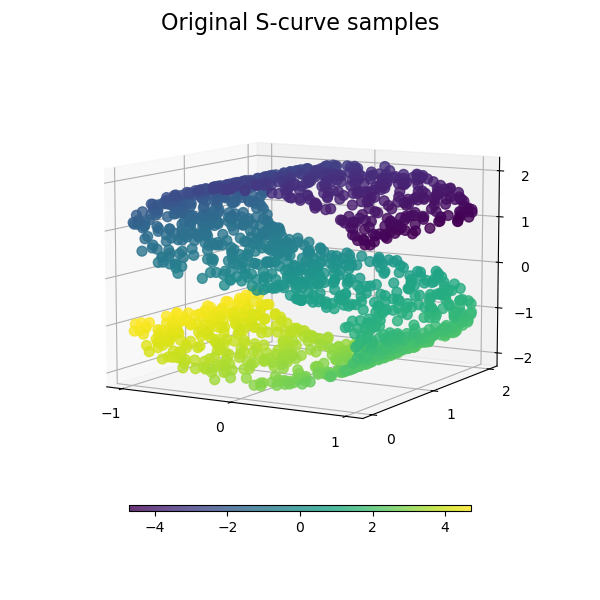
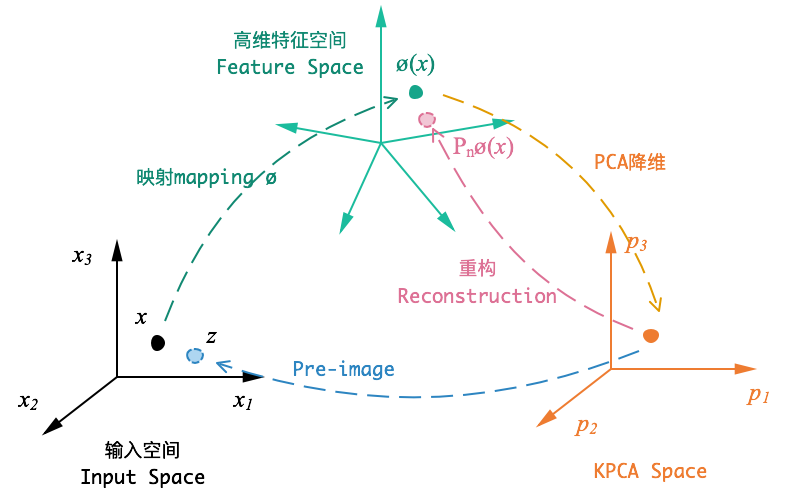
KernelPCA 算法其实很简单,只是将原始数据映射到高维空间,然后在这个高维空间进行PCA降维。
给定样本矩阵
X
=
(
x
1
⋯
x
N
)
=
(
x
11
⋯
x
1
N
x
21
⋯
x
2
N
⋮
⋱
⋮
x
p
1
⋯
x
p
N
)
X=\begin{pmatrix}\mathbf x_1&\cdots&\mathbf x_N\end{pmatrix}= \begin{pmatrix} x_{11}&\cdots&x_{1N} \\ x_{21}&\cdots&x_{2N} \\ \vdots&\ddots&\vdots \\ x_{p1}&\cdots&x_{pN} \\ \end{pmatrix}
X=(x1⋯xN)=
x11x21⋮xp1⋯⋯⋱⋯x1Nx2N⋮xpN
包含
N
N
N 个样本,
p
p
p 个特征。其中,第
j
j
j 个样本的特征向量为
x
j
=
(
x
1
j
,
x
2
j
,
⋯
,
x
p
j
)
T
\mathbf x_j=(x_{1j},x_{2j},\cdots,x_{pj})^T
xj=(x1j,x2j,⋯,xpj)T 。
将每个样本通过非线性函数
ϕ
\phi
ϕ 映射到高维空间
R
q
\R^q
Rq,得到高维空间的数据矩阵
ϕ
(
X
)
=
(
ϕ
(
x
1
)
,
⋯
,
ϕ
(
x
N
)
)
\phi(X)=(\phi(\mathbf x_1),\cdots,\phi(\mathbf x_N))
ϕ(X)=(ϕ(x1),⋯,ϕ(xN))
接下来在高维空间中对
ϕ
(
X
)
\phi(X)
ϕ(X) 进行PCA降维,在此之前,需要对其进行预处理。让我们暂时先假设矩阵
ϕ
(
X
)
\phi(X)
ϕ(X) 已经过中心化处理,即已有
∑
j
=
1
N
ϕ
(
x
j
)
=
0
\sum_{j=1}^N\phi(\mathbf x_j)=0
∑j=1Nϕ(xj)=0。
因为 ϕ ( X ) \phi(X) ϕ(X)的中心化涉及到核函数的运算,比较复杂,本文仅简单介绍下 KernelPCA 的思路。
于是,要取得降维后的方差最大值,只需对高维空间中的协方差矩阵进行特征值分解,取最大的前
p
′
p'
p′ 个特征值
ϕ
(
X
)
ϕ
(
X
)
T
W
=
W
Λ
\phi(X)\phi(X)^TW=W\Lambda
ϕ(X)ϕ(X)TW=WΛ
其中,
W
W
W 为变换矩阵,拉格朗日乘子
Λ
=
diag
(
λ
1
,
⋯
,
λ
p
)
\Lambda=\text{diag}(\lambda_1,\cdots,\lambda_p)
Λ=diag(λ1,⋯,λp)。然而,由于我们没有显式的定义映射
ϕ
\phi
ϕ,所以上式无法直接求解,必须考虑换一种方法来求解这个特征值问题。
核函数
由于在对
ϕ
(
X
)
\phi(X)
ϕ(X) 进行PCA降维时,我们只需找较大的特征值对应的特征向量,而不需要计算0特征值对应的特征向量。因此,考虑当
λ
i
≠
0
\lambda_i\neq 0
λi=0 时的情况,特征值分解方程两边右乘
Λ
−
1
\Lambda^{-1}
Λ−1
W
=
ϕ
(
X
)
ϕ
(
X
)
T
W
Λ
−
1
=
ϕ
(
X
)
C
W=\phi(X)\phi(X)^TW\Lambda^{-1}=\phi(X)C
W=ϕ(X)ϕ(X)TWΛ−1=ϕ(X)C
其中
C
=
ϕ
(
X
)
T
W
Λ
−
1
C=\phi(X)^TW\Lambda^{-1}
C=ϕ(X)TWΛ−1
将
W
W
W 带回到特征值分解方程,得到
ϕ
(
X
)
ϕ
(
X
)
T
ϕ
(
X
)
C
=
ϕ
(
X
)
C
Λ
\phi(X)\phi(X)^T\phi(X)C=\phi(X)C\Lambda
ϕ(X)ϕ(X)Tϕ(X)C=ϕ(X)CΛ
进一步,等式两边都左乘矩阵
ϕ
(
X
)
T
\phi(X)^T
ϕ(X)T
ϕ
(
X
)
T
ϕ
(
X
)
ϕ
(
X
)
T
ϕ
(
X
)
C
=
ϕ
(
X
)
T
ϕ
(
X
)
C
Λ
\phi(X)^T\phi(X)\phi(X)^T\phi(X)C=\phi(X)^T\phi(X)C\Lambda
ϕ(X)Tϕ(X)ϕ(X)Tϕ(X)C=ϕ(X)Tϕ(X)CΛ
定义矩阵
K
=
ϕ
(
X
)
T
ϕ
(
X
)
=
[
ϕ
(
x
i
)
T
ϕ
(
x
j
)
]
N
×
N
K=\phi(X)^T\phi(X)=[\phi(\mathbf x_i)^T\phi(\mathbf x_j)]_{N\times N}
K=ϕ(X)Tϕ(X)=[ϕ(xi)Tϕ(xj)]N×N
则
K
K
K 为
N
×
N
N\times N
N×N 的对称半正定矩阵。上式简化为
K
C
=
C
Λ
KC=C\Lambda
KC=CΛ
为求解上述方程,我们需要求解以下特征值问题的非零特征值:
K
c
=
λ
c
K\mathbf c=\lambda\mathbf c
Kc=λc
求解上述问题涉及到计算
ϕ
(
x
i
)
T
ϕ
(
x
j
)
\mathbf\phi(\mathbf x_i)^T\mathbf\phi(\mathbf x_j)
ϕ(xi)Tϕ(xj), 这是样本
x
i
\mathbf x_i
xi 与
x
j
\mathbf x_j
xj 映射到特征空间之后的内积。由于特征空间维数可能很高,甚至可能是无穷维,因此直接计算
ϕ
(
x
i
)
T
ϕ
(
x
j
)
\mathbf\phi(\mathbf x_i)^T\mathbf\phi(\mathbf x_j)
ϕ(xi)Tϕ(xj) 通常是困难的。为了避开这个障碍,引入核函数(kernel function)
κ
(
x
1
,
x
2
)
=
ϕ
(
x
1
)
T
ϕ
(
x
2
)
\kappa(\mathbf x_1,\mathbf x_2)=\mathbf\phi(\mathbf x_1)^T\mathbf\phi(\mathbf x_2)
κ(x1,x2)=ϕ(x1)Tϕ(x2)
即
x
i
\mathbf x_i
xi 与
x
j
\mathbf x_j
xj 在特征空间的内积等于它们在原始样本空间中通过核函数计算的结果,这称为核技巧(kernel trick)。核函数
κ
\kappa
κ 的实现方法通常有比直接构建
ϕ
(
x
)
\mathbf\phi(\mathbf x)
ϕ(x) 再算点积高效很多。
于是,通过核函数计算矩阵
K
K
K ,从而进行特征值分解。将求得的特征值排序:
λ
1
⩾
⋯
⩾
λ
N
\lambda_1\geqslant\cdots\geqslant\lambda_N
λ1⩾⋯⩾λN ,再取前
p
′
p'
p′ 个特征值对应的特征向量构成矩阵
C
=
(
c
1
⋯
c
p
′
)
C=\begin{pmatrix}\mathbf c_1&\cdots&\mathbf c_{p'}\end{pmatrix}
C=(c1⋯cp′)
注意,这里的特征向量 c j \mathbf c_j cj 只是 K K K 的特征向量,不是高维空间中协方差矩阵的特征向量。
可以看到,矩阵 K K K 需要计算所有样本间的核函数,因此该算法的计算开销十分大。
主成分计算
然而,至此仍然无法显式的计算变换矩阵
W
=
ϕ
(
X
)
C
W=\phi(X)C
W=ϕ(X)C。假设在新空间中使用标准正交基,即
W
T
W
=
I
W^TW=I
WTW=I
W
T
W
=
C
T
ϕ
(
X
)
T
ϕ
(
X
)
C
=
C
T
K
C
=
C
T
C
Λ
W^TW=C^T\phi(X)^T\phi(X)C=C^TKC=C^TC\Lambda
WTW=CTϕ(X)Tϕ(X)C=CTKC=CTCΛ
因此,求出
K
K
K 的特征值和对应的特征向量后,令
c
j
←
c
j
λ
j
\mathbf c_j\gets \frac{\mathbf c_j}{\sqrt{\lambda_j}}
cj←λjcj
即可将相应的基向量归一化。
降维后的主成分矩阵
Z
=
W
T
ϕ
(
X
)
=
C
T
ϕ
(
X
)
T
ϕ
(
X
)
=
C
T
K
Z=W^T\phi(X)=C^T\phi(X)^T\phi(X)=C^TK
Z=WTϕ(X)=CTϕ(X)Tϕ(X)=CTK
可以看到,主成分的计算也可由核函数的计算完成。
在PCA中,主成分的数量受特征数量的限制,而在KernelPCA中,主成分的数量受样本数量的限制。许多现实世界的数据集都有大量样本,在这些情况下,找到所有具有完整KernelPCA的成分是浪费计算时间,因为数据主要由前几个成分(例如n_components<=100)描述。换句话说,在KernelPCA拟合过程中特征分解的协方差矩阵的有效秩比其大小小得多。在这种情况下,近似特征求解器可以以非常低的精度损失提供加速。
因子分析
因子分析(Factor Analysis,FA)和PCA类似,也采用矩阵分解方法来降维。它通过寻找一组潜在的因子来解释已观测到变量间的关系。
基本形式
假设
p
p
p维样本
x
=
(
x
1
,
x
2
,
⋯
,
x
p
)
T
\mathbf x=(x_1,x_2,\cdots,x_p)^T
x=(x1,x2,⋯,xp)T 可由几个相互独立的潜在因子(latent factor)线性近似
x
=
μ
+
W
f
+
e
\mathbf x=\mu+W\mathbf f+\mathbf e
x=μ+Wf+e
因子向量 f = ( f 1 , f 2 , ⋯ , f k ) T , ( k ⩽ p ) \mathbf f=(f_1,f_2,\cdots,f_k)^T, (k\leqslant p) f=(f1,f2,⋯,fk)T,(k⩽p), f \mathbf f f的分量 f i f_i fi称为公共因子(common factor)。随机向量 e = ( e 1 , e 2 , ⋯ , e p ) T \mathbf e=(e_1,e_2,\cdots,e_p)^T e=(e1,e2,⋯,ep)T , e \mathbf e e的分量 e i e_i ei称为特殊因子(specific factor)。矩阵 W = ( w i j ) p × k W=(w_{ij})_{p\times k} W=(wij)p×k 称为因子载荷矩阵(factor loading),元素 w i j w_{ij} wij是 x \mathbf x x的第 i i i个分量 x i x_i xi在第 j j j个因子 f j f_j fj上的载荷。
通常假设公共因子服从正态分布
f
∼
N
(
0
,
I
)
\mathbf f\sim N(0,\mathbf I)
f∼N(0,I)
且相互独立。为确保公共因子唯一,假定他们都是单位方差。
特殊因子服从正态分布
e
∼
N
(
0
,
Λ
)
,
Λ
=
diag
(
σ
1
2
,
σ
2
2
,
⋯
,
σ
p
2
)
\mathbf e\sim N(0,\Lambda), \quad\Lambda=\text{diag}(\sigma^2_1,\sigma^2_2,\cdots,\sigma^2_p)
e∼N(0,Λ),Λ=diag(σ12,σ22,⋯,σp2)
容易知道
x
∼
N
(
μ
,
W
W
T
+
Λ
)
\mathbf x\sim N(\mu,WW^T+\Lambda)
x∼N(μ,WWT+Λ)
于是 v a r ( x i ) = ∑ j = 1 k w i j 2 + σ i 2 var(x_i)=\sum_{j=1}^kw_{ij}^2+\sigma_i^2 var(xi)=∑j=1kwij2+σi2 ,可以看出的 x i x_i xi方差由两部分构成。记 g i 2 = ∑ j = 1 k w i j 2 g_i^2=\sum_{j=1}^kw_{ij}^2 gi2=∑j=1kwij2 ,反映了公共因子 f j f_j fj对 x i x_i xi的影响。
因为特殊因子的方差阵是对角阵,所以样本任意两个分量的协方差 c o v ( x s , x t ) = ∑ i = 1 k w s i w t i cov(x_s,x_t)=\sum_{i=1}^kw_{si}w_{ti} cov(xs,xt)=∑i=1kwsiwti 仅由公共因子决定, 不含特殊因子影响。
参数估计
因子模型的未知参数是载荷矩阵 W W W和特殊因子方差 Λ \Lambda Λ,可以用主成分法、极大似然法、主因子法估计。