目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
5.完整程序
1.程序功能描述
基于Itô扩散过程的交易策略偏微分方程,提出了一种确定Itô扩散过程。通过根据的第一次通过时间来确定问题在这个过程中,我们推导出交易长度的分布函数和密度函数,并使用它们函数来计算策略的预期交易频率。
2.测试软件版本以及运行结果展示
MATLAB2022A版本运行

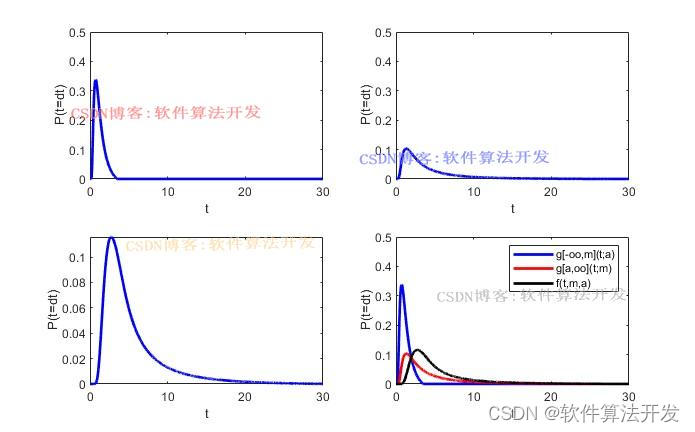
(完整程序运行后无水印)
3.核心程序
..............................................................
for x = 1:N
x
t = TT(x);
g2(x) = 1/sqrt(2*pi*delta*delta*t)*exp(-(X-alpha*xo*t)^2/(2*delta*delta*t))*(1/2/t+(2*(X-alpha*xo*t)*alpha*xo+(X-alpha*xo*t)^2/t)/2/delta/delta/t);
if g2(x)<0;
g2(x)=0;
end
end
subplot(222);
plot(TT,g2,'b-','linewidth',2);
xlabel('t');
ylabel('P(t=dt)');
axis([0,T,0,0.5]);
%计算卷积;
f0 = conv(g1,g2);
f = f0(1:N)/(N/100);
subplot(223);
plot(TT,f,'b-','linewidth',2);
xlabel('t');
ylabel('P(t=dt)');
% axis([0,T,0,0.5]);
subplot(224);
plot(TT,g1,'b','linewidth',2);
hold on;
plot(TT,g2,'r','linewidth',2);
hold on;
plot(TT,f,'k','linewidth',2);
xlabel('t');
ylabel('P(t=dt)');
axis([0,T,0,0.5]);
legend('g[-oo,m](t;a)','g[a,oo](t;m)','f(t,m,a)');
set(gcf,'position',[200,200,800,400]);
clear all;
16_026m4.本算法原理
基于Itô扩散过程的交易策略通常涉及金融衍生品定价和风险管理,其中最核心的是利用随机微分方程(SDEs)来建模资产价格动态,并进一步求解相关的偏微分方程(PDEs),以确定最优交易策略或资产的公平价值。




基于Itô扩散过程的交易策略设计是一个融合了随机过程理论、偏微分方程理论及优化理论的复杂领域。通过构建合适的模型并解决相应的偏微分方程,可以为投资者提供在不确定市场环境中制定最优投资策略的工具。
5.完整程序
VVV