动态规划刷题复习

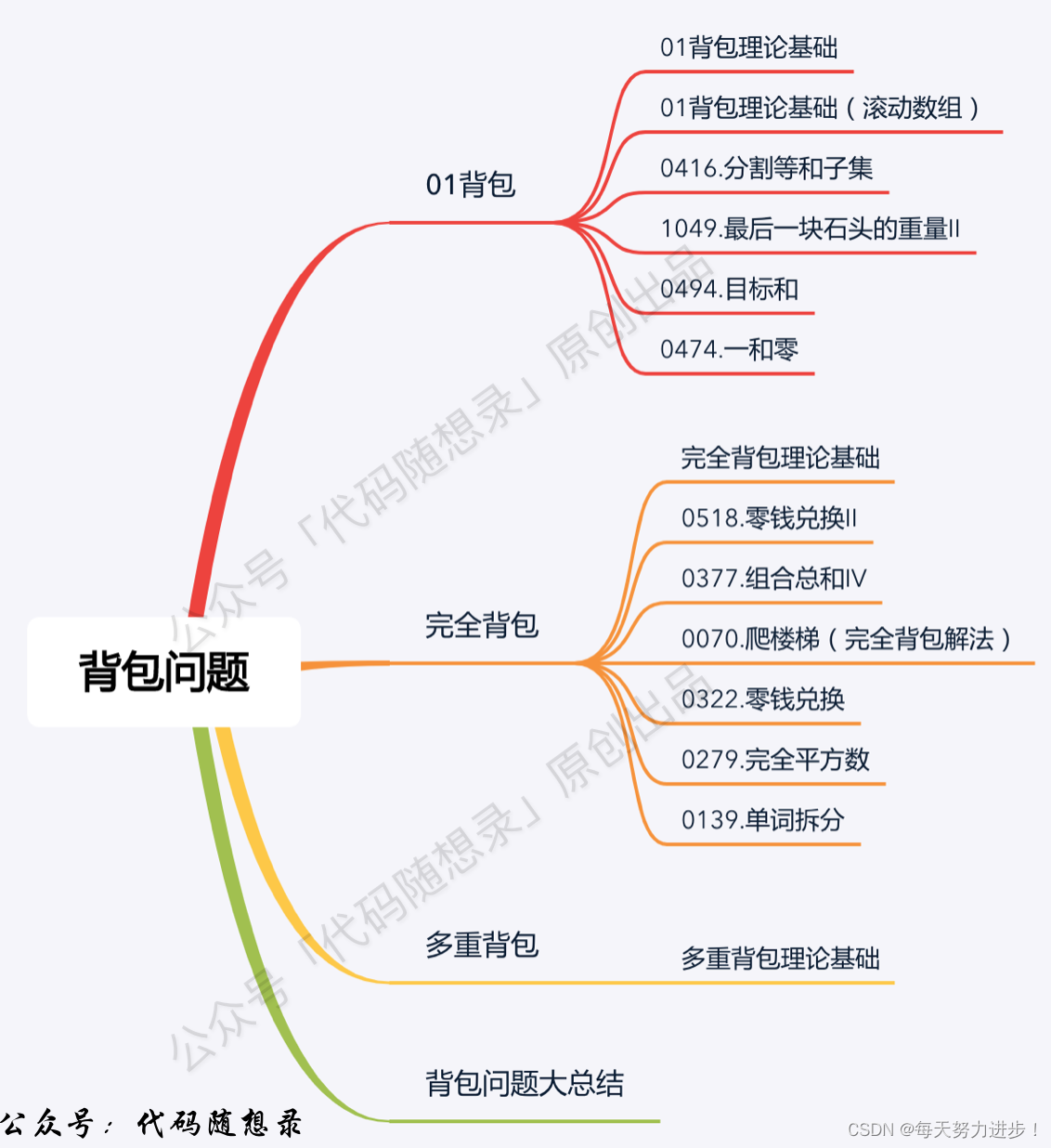
一、01背包

1. 416. 分割等和子集
2. 1049. 最后一块石头的重量 II
3. 494. 目标和
4. 474. 一和零

416. 分割等和子集

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum=0;
        for(int i=0;i<nums.size();i++) {
            sum+=nums[i];
        }
        if(sum%2!=0)
            return false;
        vector<int> dp(sum/2+1,0);
        for(int i=0;i<nums.size();i++) {
            for(int j=sum/2;j>=nums[i];j--) {
                dp[j] = max(dp[j],dp[j-nums[i]]+nums[i]);
            }
        }
        if(dp[sum/2]==sum/2)
            return true;
        else
            return false;
        

    }
};

1049. 最后一块石头的重量 II

class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        //将所有的石头分为两堆，这两队的重量尽可能地相近，最后用这两堆的重量之差的绝对值来表示最后的结果
        int sum=0;
        for(int i=0;i<stones.size();i++) {
            sum+=stones[i];
        }
        int target = sum/2;   // /是向下取整， sum-target >= target

        vector<int> dp(target+1,0);
        for(int i=0;i<stones.size();i++) {
            for(int j=target;j>=stones[i];j--) {
                dp[j] = max(dp[j], dp[j-stones[i]]+stones[i]);
            }
        }
        return sum-dp[target] - dp[target];
    }
};

494. 目标和

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        //这个题，动规比较隐含，需要自己找一下这个背包容量(sum+target)/2;
        //所有元素的和为sum，x表示加法运算的和，减法背包的容量sum-x，target = x - (sum-x); 就得到了x的表达
        int sum=0;
        for(int i=0;i<nums.size();i++) 
            sum+=nums[i];
        int x = (sum+target)/2;
        vector<int> dp(x+1,0);
        //这个初始条件很重要，当初始化为全零的时候结果为0
        dp[0]=1;
        for(int i=0;i<nums.size();i++) {
            for(int j=x;j>=nums[i];j--) {
                //这里这个问总和的题，需要用+=,
                //不复习有点忘了。
                dp[j] += dp[j-nums[i]];
            }
        }
        return dp[x];
    }
};

474. 一和零

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {

        vector<vector<int>>  dp(m+1,vector<int>(n+1,0));
        //先取出来字符串数组中的每个字符串
        for(string s : strs){
            //统计这个字符串中出现了多少个0和1
            int num_0=0,num_1=0;    
            for(char c : s) {
                if(c=='0')
                    num_0++;
                else if(c=='1')
                    num_1++;
            }
            for(int i=m;i>=num_0;i--) {
                for(int j=n;j>=num_1;j--) {
                    dp[i][j] = max(dp[i][j], dp[i-num_0][j-num_1]+1);
                }
            }
        }
        return dp[m][n];
    }
};

二、完全背包问题

1. 518 零钱兑换Ⅱ
   题目要求：符合 32 位整数范围；
2. 377.组合总和Ⅳ
3. 70 爬楼梯 完全背包问题版本
4. 322.零钱兑换
5. 279.完全平方数
   for循环中 j的界限从1开始
6. 139.单词拆分
   这个题对unordered_set的使用以及dp[i]的更新还是不熟练

518 零钱兑换Ⅱ

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount+1,0);
        //问组合数的问题，dp[0]初始化为1
        dp[0]=1;
        for(int i=0;i<coins.size();i++) {
            //完全背包问题，不要求仅出现一次，内层循环不用逆序
            for(int j=coins[i];j<=amount;j++) {
                //组合问题 +=
                dp[j] += dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
};

377.组合总和Ⅳ

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        //排列问题
        vector<int> dp(target+1,0);
        dp[0] = 1;
        for(int i=0;i<=target;i++) {
            for(int j=0;j<nums.size();j++) {
                //排列问题：
                //外层遍历 背包容量，内层遍历物品
                //要先判断这个背包容量和当前物品大小
                //以及满足：符合 32 位整数范围（不能超过INT_MAX）
                if(nums[j]<=i && dp[i] < INT_MAX-dp[i-nums[j]])
                    dp[i] += dp[i-nums[j]];
            }
        }
        return dp[target];
    }
};

70 爬楼梯 完全背包问题版本

class Solution {
public:
    int climbStairs(int n) {
        //把这个问题看作是完全背包问题，1和2可以无限选择
        vector<int> dp(n+1,0);
        //问总数的，dp[0]初始化为1
        dp[0]=1;
        //最少上一层台阶
        for(int i=1;i<=n;i++) {
            //这里物品遍历选择只有1，2
            for(int j=1;j<=2;j++) {
                if(i-j>=0)
                    //+=
                    dp[i] += dp[i-j];
            }
        }
        return dp[n];
    }
};

322.零钱兑换

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        //找dp[amount]最小，初始化定义为INT_MAX
        vector<int> dp(amount+1,INT_MAX);
        //dp[0]的初始化需要修改为0,
        dp[0]=0;
        //这里不用考虑组合还是排列，这个遍历顺序就是正序就行
        for(int i=0;i<coins.size();i++) {
            for(int j=coins[i];j<=amount;j++) {
                if(dp[j-coins[i]]!=INT_MAX)
                    dp[j] = min(dp[j],dp[j-coins[i]]+1);
            }
        }
        //如果凑不到这个总金额的话，这个值没有修改，就返回-1
        if(dp[amount]==INT_MAX)
            return -1;
        return dp[amount];
    }
};

279.完全平方数

class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1,INT_MAX);
        dp[0]=0;
        //外层遍历“背包”
        for(int i=0;i<=n;i++) {
            //内层，控制平方数不能大于i
            //j从0开始会报错：runtime error 发生溢出
            for(int j=1;j*j<=i;j++) {
                dp[i] = min(dp[i-j*j]+1,dp[i]);
            }
        }
        return dp[n];
    }
};

139.单词拆分

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        //unordered_set这个容器不熟悉

        //无序集合，值唯一，可使用find()函数来查找元素（在这里是查找单词）
        unordered_set<string> wordSet(wordDict.begin(),wordDict.end());
        vector<bool> dp(s.size()+1,false);
        dp[0]=true;
        //这里的处理逻辑：
        for(int i=1;i<=s.size();i++) {
            //这里的j实际上是从0开始找到第一个单词结束的末尾，然后把j- i-j这一段单词复制出来
            for(int j=0;j<i;j++) {
                string substr1 = s.substr(j,i-j);
                //这里这个dp[j]很关键，
                //找到上一个单词的结尾位置并且新单词也在字典中，才能为true;
                if(wordSet.find(substr1)!=wordSet.end() && dp[j])
                    dp[i] = true;
            }
        }
        return dp[s.size()];
    }
};