CNN学习（7）：用C++实现简单不同参数的卷积模型

news2024/10/7 15:22:11

目录

一、参数说明和计算公式

1、符号约定

2、输出大小计算公式

二、不同类型的卷积

1、输入3*3*1，卷积核3*3*1，输出1*1*1

（1）实现代码

（2）代码说明

2、输入4*4*1，卷积核3*3*1，步长1*1，输出2*2*1

（1）实现代码

（2）代码说明

3、输入4*4*1，卷积核2*2*1，步长2*2，输出2*2*1

（1）实现代码

4、输入4*4*1，卷积核3*3*1，步长1*1，padding为1*1，输出2*2*1

​编辑

（1）实现代码

（2）代码说明

5、输入4*4*2，卷积核3*3*2，步长1*1，padding为1*1，输出2*2*1

（1）实现代码

6、输入4*4*1，卷积核3*3*1，卷积核个数2，步长1*1，padding为1*1，输出2*2*1

（1）实现代码

（2）代码说明

7、输入4*4*2，卷积核3*3*2，步长1*1，padding为1*1，膨胀系数2，输出2*2*2

三、可执行的卷积操作代码

参考资料：

(图解)一步一步使用CPP实现深度学习中的卷积 - GiantPandaCV

其实在上述链接里已经写的非常详细了，为了便于后续理解和学习，所以写个理解的备忘录。

一、参数说明和计算公式

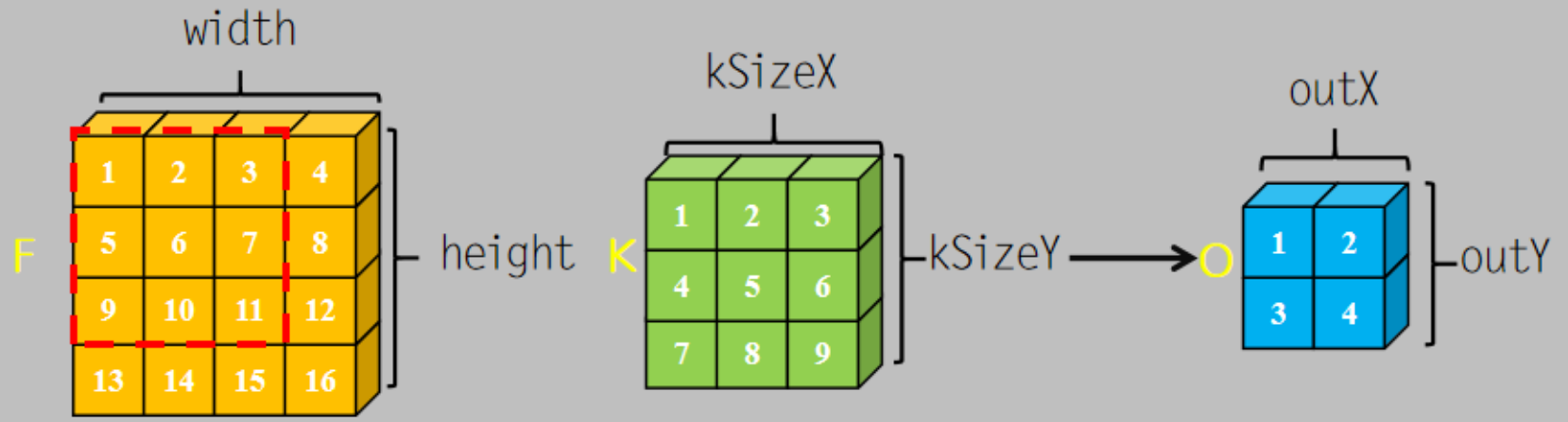
1、符号约定

F[] 为输入;
width 为输入的宽;
height 为输入的高;
channel 为输入的通道;

K[] 为 kernel;
kSizeX 为 kernel 的宽;
kSizeY 为 kernel 的高;
filters 为 kernel 的个数;
padX 为水平方向的填充；
padY 为垂直方向的填充；
strideX 为水平方向的步长；
strideY 为垂直方向的步长；


O[] 为输出;
outW 为输出的宽;
outH 为输出的高;
outChannel 为输出的通道;

2、输出大小计算公式

int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

公式说明：

  • height + 2 * padY: 首先，将输入图像的高度加上两倍的填充量，这是因为填充是对称地加在图像的顶部和底部。

  • dilationY * (kSizeY - 1): 这是计算卷积核中除了中心元素外，其他元素之间的总间隔。kSizeY - 1表示卷积核的高度减去中心元素，乘以膨胀系数dilationY，得到这些元素之间的间隔数。

  • dilationY * (kSizeY - 1) + 1: 将上述间隔数加上1，是因为我们还要包括卷积核的中心元素。

  • (height + 2 * padY - (dilationY * (kSizeY - 1) + 1)): 这个表达式计算了在考虑填充和膨胀后，输入图像实际上被卷积核覆盖的区域的高度。

  • / strideY: 将上述计算得到的高度除以步长，得到在垂直方向上卷积核可以覆盖的步数。

  • + 1: 最后，由于输出的高度至少要有一个元素，即使计算结果为0，我们也需要加1，以确保输出尺寸至少为1。

二、不同类型的卷积

1、输入3*3*1，卷积核3*3*1，输出1*1*1

（1）实现代码

封装成demo0()，main()函数可直接调用

void demo0()
{
    float F[] = {1,2,3,4,5,6,7,8,9};
    float K[] = {1,2,3,4,5,6,7,8,9};
    float O = 0;

    int width  = 3;
    int height = 3;
    int kSizeX = 3;
    int kSizeY = 3;

    for(int m=0;m<kSizeY;m++)
    {
        for(int n=0;n<kSizeX;n++)
        {
            O+=K[m*kSizeX+n]*F[m*width+n];
        }
    }

    std::cout<<O<<" ";
}

（2）代码说明

  1. 前面都是定义输入矩阵和卷积核，同时定义一个浮点数变量O并初始化为0，用于累加结果。
  2. 两个嵌套循环遍历卷积核的每个元素：
    1. for(int m=0; m<kSizeY; m++)：外层循环遍历卷积核的高度。
    2. for(int n=0; n<kSizeX; n++)：内层循环遍历卷积核的宽度。
    3. 嵌套循环内部，O += K[m*kSizeX + n] * F[m*width + n];用来执行卷积操作。这行代码将卷积核的当前元素 K[m*kSizeX + n] 与输入矩阵的对应元素 F[m*width + n] 相乘，并将结果累加到 O 中【其中位置是相同的，m只是用来决定以kSize为单位的轮次】。

2、输入4*4*1，卷积核3*3*1，步长1*1，输出2*2*1

（1）实现代码

void demo1()
{
    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    float K[] = {1,2,3,4,5,6,7,8,9};
    float O[] = {0,0,0,0};

    int padX = 0;
    int padY = 0;

    int dilationX = 1;
    int dilationY = 1;

    int strideX  = 1;
    int strideY  = 1;

    int width = 4;
    int height = 4;

    int kSizeX = 3;
    int kSizeY = 3;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    for(int i=0;i<outH;i++)
    {
        for(int j=0;j<outW;j++)
        {
            for(int m=0;m<kSizeY;m++)
            {
                for(int n=0;n<kSizeX;n++)
                {
                    O[i*outW+j]+=K[m*kSizeX+n]*F[(m+i)*width+(n+j)];
                }
            }
        }
    }

    for (int i = 0; i < outH; ++i)
    {
        for (int j = 0; j < outW; ++j)
        {
            std::cout<<O[i*outW+j]<<" ";
        }
        std::cout<<std::endl;
    }
}

（2）代码说明

  1. 前面都是定义输入矩阵和卷积核，同时定义一个浮点数变量O并初始化【和前面后面一样，都是先计算出来输出结果的大小，然后再执行】，用于累加结果。
  2. 四个嵌套循环开始进行卷积计算：
    1. 外层两个循环遍历输出特征图的每个位置。
    2. 内层两个循环遍历卷积核的每个元素。

  3. 在内层循环中，计算卷积核覆盖的输入特征图区域的加权和，并将结果累加到输出特征图的相应位置。

3、输入4*4*1，卷积核2*2*1，步长2*2，输出2*2*1

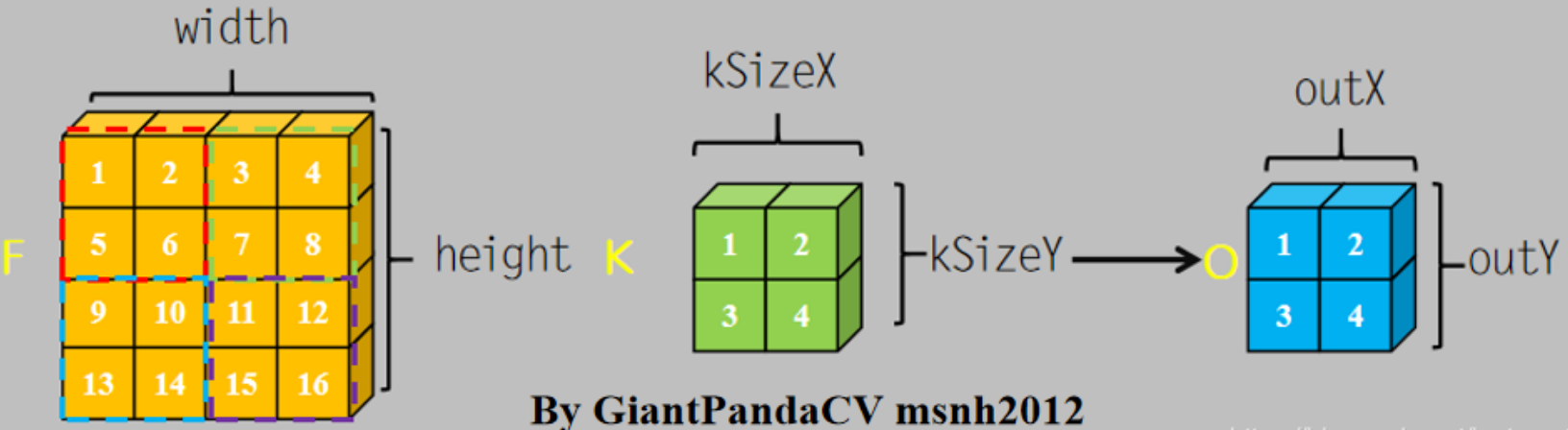
（1）实现代码

void demo2()
{
    // (height + 2 * paddingY - (dilationY * (kSizeY - 1) + 1)) / strideY + 1;
    // (width + 2 * paddingX - (dilationX * (kSizeX - 1) + 1)) / strideX + 1;

    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    float K[] = {1,2,3,4};
    //float K[] = {1,2,3,4,5,6,7,8,9};
    float O[] = {0,0,0,0};

    int padX = 0;
    int padY = 0;

    int dilationX = 1;
    int dilationY = 1;

    int strideX  = 2;
    int strideY  = 2;

    int width = 4;
    int height = 4;

    int kSizeX = 2;
    int kSizeY = 2;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    for(int i=0;i<outH;i++)
    {
        for(int j=0;j<outW;j++)
        {
            for(int m=0;m<kSizeY;m++)
            {
                for(int n=0;n<kSizeX;n++)
                {
                    O[i*outW+j]+=K[m*kSizeX+n]*F[(m+i*strideY)*width+(n+j*strideX)];
                }
            }
        }
    }

    for (int i = 0; i < outH; ++i)
    {
        for (int j = 0; j < outW; ++j)
        {
            std::cout<<O[i*outW+j]<<" ";
        }
        std::cout<<std::endl;
    }
}

这个和上一段代码解释相同，只不过步长和卷积核大小有改变。

4、输入4*4*1，卷积核3*3*1，步长1*1，padding为1*1，输出2*2*1

（1）实现代码

void demo3()
{
    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    float K[] = {1,2,3,4,5,6,7,8,9};
    float O[] = {0,0,0,0};

    int padX = 1;
    int padY = 1;

    int dilationX = 1;
    int dilationY = 1;

    int strideX  = 2;
    int strideY  = 2;

    int width = 4;
    int height = 4;

    int kSizeX = 3;
    int kSizeY = 3;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    for(int i=0;i<outH;i++)
    {
        for(int j=0;j<outW;j++)
        {
            for(int m=0;m<kSizeY;m++)
            {
                for(int n=0;n<kSizeX;n++)
                {
                    float fVal = 0;  
                    //考虑边界强情况
                    if((n+j*strideX-padX)>-1&&(m+i*strideY-padY>-1)&&(n+j*strideX-padX)<=width&&(m+i*strideY-padY>-1)<=height) 
                    {
                        fVal = F[(m+i*strideY-padX)*width+(n+j*strideX-padY)];
                    }
                    O[i*outW+j]+=K[m*kSizeX+n]*fVal;
                }
            }
        }
    }

    for (int i = 0; i < outH; ++i)
    {
        for (int j = 0; j < outW; ++j)
        {
            std::cout<<O[i*outW+j]<<" ";
        }
        std::cout<<std::endl;
    }
}

（2）代码说明

按照正常计算输出规模公式计算的话，应该输出是4*4*1。但是考虑到边界墙问题。

if 语句块用来检查当前卷积核的 m 和 n 索引是否在输入特征图的边界内。这里考虑了填充（padding）的情况：

  • (n+j*strideX - padX) 计算了卷积核的左边界在输入特征图上的索引。
  • (m+i*strideY - padY) 计算了卷积核的上边界在输入特征图上的索引。
  • 条件 > -1 确保索引不会是负数。
  • 条件 <= width 和 <= height 确保索引不会超出输入特征图的边界。

5、输入4*4*2，卷积核3*3*2，步长1*1，padding为1*1，输出2*2*1

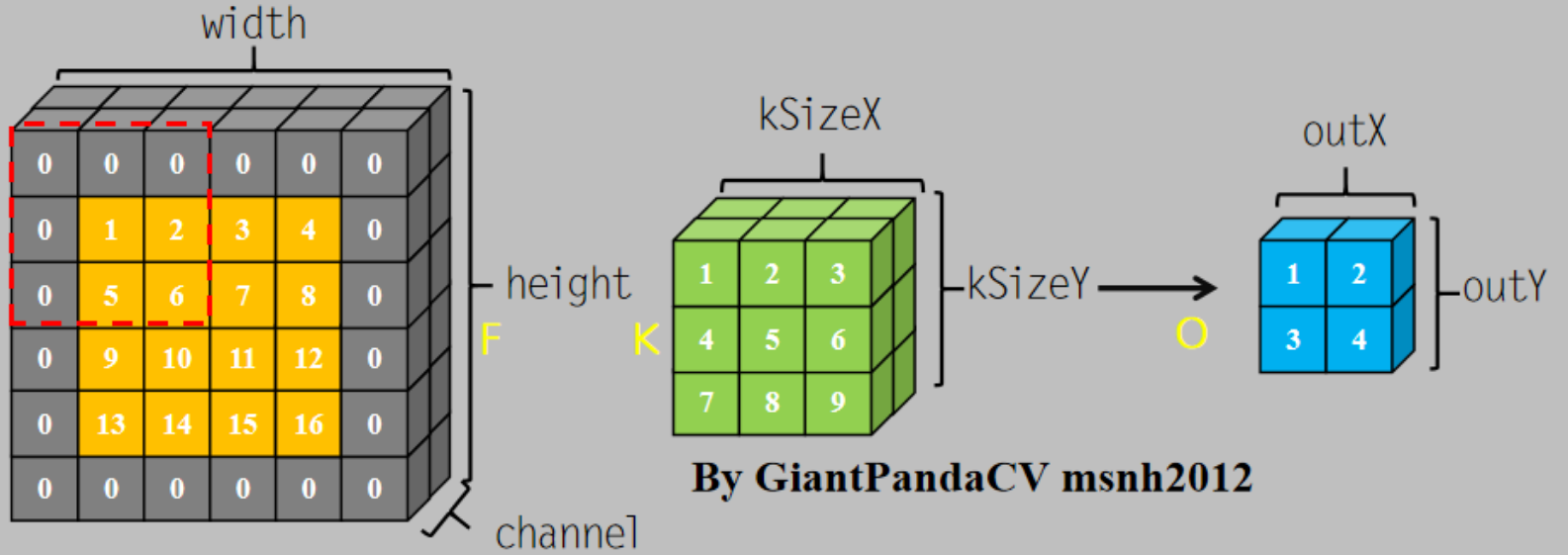
其中依旧考虑了边界墙问题。

（1）实现代码

void demo4()
{
    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    float K[] = {1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9};
    float O[] = {0,0,0,0};

    int padX = 1;
    int padY = 1;

    int dilationX = 1;
    int dilationY = 1;

    int strideX  = 2;
    int strideY  = 2;

    int width = 4;
    int height = 4;

    int kSizeX = 3;
    int kSizeY = 3;

    int channel = 2;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    for (int c = 0; c < channel; ++c)
    {
        for(int i=0;i<outH;i++)
        {
            for(int j=0;j<outW;j++)
            {
                for(int m=0;m<kSizeY;m++)
                {
                    for(int n=0;n<kSizeX;n++)
                    {
                        float fVal = 0;
                        if((n+j*strideX-padX)>-1&&(m+i*strideY-padY>-1)&&(n+j*strideX-padX)<=width&&(m+i*strideY-padY>-1)<=height)
                        {
                            fVal = F[c*width*height + (m+i*strideY-padX)*width+(n+j*strideX-padY)];
                        }
                        O[i*outW+j]+=K[c*kSizeX*kSizeY+m*kSizeX+n]*fVal;
                    }
                }
            }
        }
    }

    for (int i = 0; i < outH; ++i)
    {
        for (int j = 0; j < outW; ++j)
        {
            std::cout<<O[i*outW+j]<<" ";
        }
        std::cout<<std::endl;
    }
}

6、输入4*4*1，卷积核3*3*1，卷积核个数2，步长1*1，padding为1*1，输出2*2*1

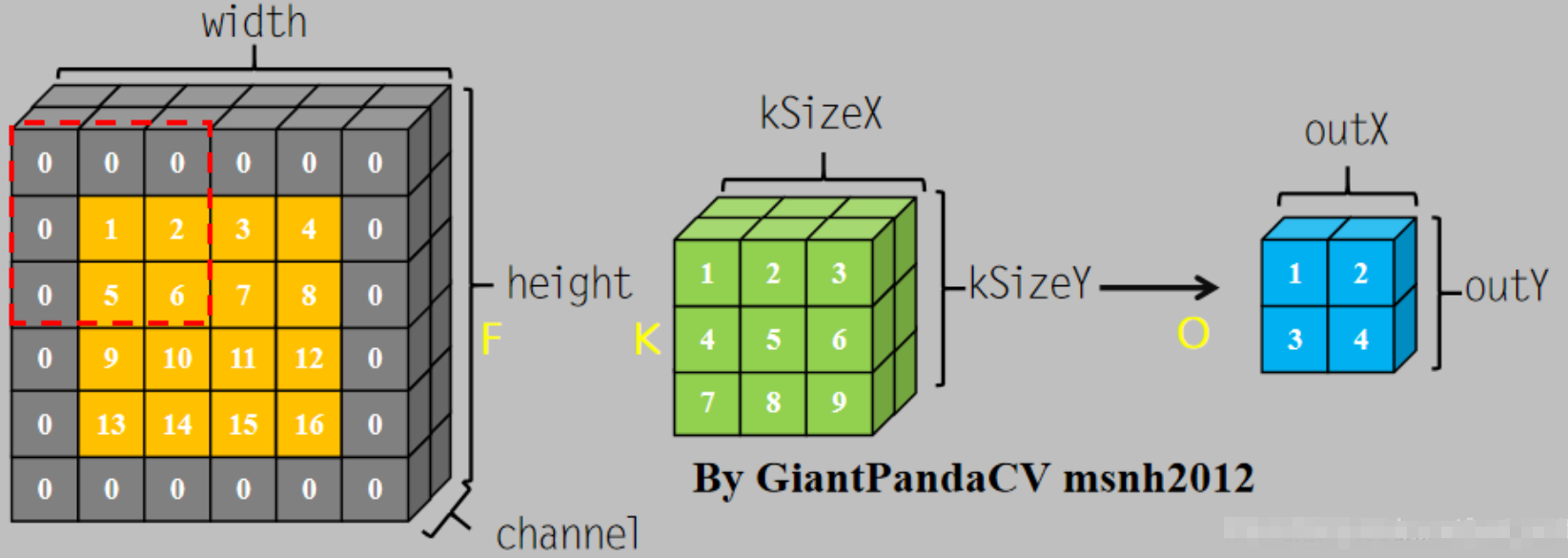
（1）实现代码

void demo5()
{
    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    float K[] = {1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9,
                 1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9
                };
    float O[] = {0,0,0,0,0,0,0,0};

    int padX = 1;
    int padY = 1;

    int dilationX = 1;
    int dilationY = 1;

    int strideX  = 2;
    int strideY  = 2;

    int width = 4;
    int height = 4;

    int kSizeX = 3;
    int kSizeY = 3;

    int channel = 2;

    int filters = 2;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    int outC = filters;

    for (int oc = 0; oc < outC; ++oc)
    {
        for (int c = 0; c < channel; ++c)
        {
            for(int i=0;i<outH;i++)
            {
                for(int j=0;j<outW;j++)
                {
                    for(int m=0;m<kSizeY;m++)
                    {
                        for(int n=0;n<kSizeX;n++)
                        {
                            float fVal = 0;
                            if((n+j*strideX-padX)>-1&&(m+i*strideY-padY>-1)&&(n+j*strideX-padX)<=width&&(m+i*strideY-padY>-1)<=height)
                            {
                                fVal = F[c*width*height + (m+i*strideY-padX)*width+(n+j*strideX-padY)];
                            }
                            O[oc*outH*outW+i*outW+j]+=K[oc*outC*kSizeX*kSizeY+c*kSizeX*kSizeY+m*kSizeX+n]*fVal;
                        }
                    }
                }
            }
        }
    }

    for (int oc = 0; oc < outC; ++oc)
    {
        for (int i = 0; i < outH; ++i)
        {
            for (int j = 0; j < outW; ++j)
            {
                std::cout<<O[oc*outH*outW+i*outW+j]<<" ";
            }
            std::cout<<std::endl;
        }
        std::cout<<std::endl<<std::endl;
    }
}

（2）代码说明

  1. 六个嵌套循环实现了卷积操作：

    • 最外层循环遍历输出特征图的每个通道。
    • 第二个循环遍历输入特征图的每个通道。
    • 第三个和第四个循环遍历输出特征图的每个元素。
    • 最内层两个循环遍历每个卷积核的元素。

  2. 在最内层循环中，首先检查当前卷积核的索引是否在输入特征图的边界内，如果是，则从输入特征图中取出相应的元素 fVal。

  3. 然后，将 fVal 与对应卷积核的元素相乘，并将结果累加到输出特征图的对应位置。

7、输入4*4*2，卷积核3*3*2，步长1*1，padding为1*1，膨胀系数2，输出2*2*2

void demo6()
{
    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    float K[] = {1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9,
                 1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9
                };
    float O[] = {0,0,0,0,0,0,0,0};

    int padX = 1;
    int padY = 1;

    int dilationX = 2;
    int dilationY = 2;

    int strideX  = 1;
    int strideY  = 1;

    int width = 4;
    int height = 4;

    int kSizeX = 3;
    int kSizeY = 3;

    int channel = 2;

    int filters = 2;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    int outC = filters;

    for (int oc = 0; oc < outC; ++oc)
    {
        for (int c = 0; c < channel; ++c)
        {
            for(int i=0;i<outH;i++)
            {
                for(int j=0;j<outW;j++)
                {
                    for(int m=0;m<kSizeY;m++)
                    {
                        for(int n=0;n<kSizeX;n++)
                        {
                            float fVal = 0;
                            if( ((n+j*strideX)*dilationX-padX)>-1 && ((m+i*strideY)*dilationY-padY)>-1&&
                               ((n+j*strideX)*dilationX-padX)<=width && ((m+i*strideY)*dilationY-padY>-1)<=height)
                            {
                                fVal = F[c*width*height + ((m+i*strideY)*dilationX-padX)*width+((n+j*strideX)*dilationY-padY)];
                            }
                            O[oc*outH*outW+i*outW+j]+=K[oc*outC*kSizeX*kSizeY+c*kSizeX*kSizeY+m*kSizeX+n]*fVal;
                        }
                    }
                }
            }
        }
    }

    for (int oc = 0; oc < outC; ++oc)
    {
        for (int i = 0; i < outH; ++i)
        {
            for (int j = 0; j < outW; ++j)
            {
                std::cout<<O[oc*outH*outW+i*outW+j]<<" ";
            }
            std::cout<<std::endl;
        }
        std::cout<<std::endl;
    }
}

三、可执行的卷积操作代码

#include <iostream>

void demo0()    //输入3*3*1，卷积核3*3*1，输出为1*1*1
{
    float F[] = {1,2,3,4,5,6,7,8,9};
    float K[] = {1,2,3,4,5,6,7,8,9};
    float O = 0;

    int width  = 3;
    int height = 3;
    int kSizeX = 3;
    int kSizeY = 3;

    for(int m=0;m<kSizeY;m++)
    {
        for(int n=0;n<kSizeX;n++)
        {
            O+=K[m*kSizeX+n]*F[m*width+n];
        }
    }
    std::cout<<O<<" ";
}

void demo1()    //输入4*4*1，卷积核3*3*1，步长为1*1，no padding，输出为1*1*1
{
    //计算公式
    // (height + 2 * paddingY - (dilationY * (kSizeY - 1) + 1)) / strideY + 1;
    // (width + 2 * paddingX - (dilationX * (kSizeX - 1) + 1)) / strideX + 1;

    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    float K[] = {1,2,3,4,5,6,7,8,9};
    float O[] = {0,0,0,0};

    int padX = 0;
    int padY = 0;

    int dilationX = 1;
    int dilationY = 1;

    int strideX  = 1;
    int strideY  = 1;

    int width = 4;
    int height = 4;

    int kSizeX = 3;
    int kSizeY = 3;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    for(int i=0;i<outH;i++)
    {
        for(int j=0;j<outW;j++)
        {
            for(int m=0;m<kSizeY;m++)
            {
                for(int n=0;n<kSizeX;n++)
                {
                    O[i*outW+j]+=K[m*kSizeX+n]*F[(m+i)*width+(n+j)];
                    /* int inputIndex = (i * strideY + m) * width + (j * strideX + n);
                    O[i * outW + j] += K[m * kSizeX + n] * F[inputIndex]; */
                }
            }
        }
    }

    for (int i = 0; i < outH; ++i)
    {
        for (int j = 0; j < outW; ++j)
        {
            std::cout<<O[i*outW+j]<<" ";
        }
        std::cout<<std::endl;
    }
}

void demo2()
{

    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    float K[] = {1,2,3,4};
    //float K[] = {1,2,3,4,5,6,7,8,9};
    float O[] = {0,0,0,0};

    int padX = 0;
    int padY = 0;

    int dilationX = 1;
    int dilationY = 1;

    int strideX  = 2;
    int strideY  = 2;

    int width = 4;
    int height = 4;

    int kSizeX = 2;
    int kSizeY = 2;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    for(int i=0;i<outH;i++)
    {
        for(int j=0;j<outW;j++)
        {
            for(int m=0;m<kSizeY;m++)
            {
                for(int n=0;n<kSizeX;n++)
                {
                    O[i*outW+j]+=K[m*kSizeX+n]*F[(m+i*strideY)*width+(n+j*strideX)];
                }
            }
        }
    }

    for (int i = 0; i < outH; ++i)
    {
        for (int j = 0; j < outW; ++j)
        {
            std::cout<<O[i*outW+j]<<" ";
        }
        std::cout<<std::endl;
    }
}

void demo3()
{

    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    //float K[] = {1,2,3,4};
    float K[] = {1,2,3,4,5,6,7,8,9};
    float O[] = {0,0,0,0};

    int padX = 1;
    int padY = 1;

    int dilationX = 1;
    int dilationY = 1;

    int strideX  = 2;
    int strideY  = 2;

    int width = 4;
    int height = 4;

    int kSizeX = 3;
    int kSizeY = 3;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    for(int i=0;i<outH;i++)
    {
        for(int j=0;j<outW;j++)
        {
            for(int m=0;m<kSizeY;m++)
            {
                for(int n=0;n<kSizeX;n++)
                {
                    float fVal = 0;
                    //考虑边界强情况
                    if((n+j*strideX-padX)>-1&&(m+i*strideY-padY>-1)&&(n+j*strideX-padX)<=width&&(m+i*strideY-padY>-1)<=height)
                    {
                        fVal = F[(m+i*strideY-padX)*width+(n+j*strideX-padY)];
                    }
                    O[i*outW+j]+=K[m*kSizeX+n]*fVal;
                }
            }
        }
    }

    for (int i = 0; i < outH; ++i)
    {
        for (int j = 0; j < outW; ++j)
        {
            std::cout<<O[i*outW+j]<<" ";
        }
        std::cout<<std::endl;
    }
}

void demo4()
{
    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    //float K[] = {1,2,3,4};
    float K[] = {1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9};
    float O[] = {0,0,0,0};

    int padX = 1;
    int padY = 1;

    int dilationX = 1;
    int dilationY = 1;

    int strideX  = 2;
    int strideY  = 2;

    int width = 4;
    int height = 4;

    int kSizeX = 3;
    int kSizeY = 3;

    int channel = 2;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    for (int c = 0; c < channel; ++c)
    {
        for(int i=0;i<outH;i++)
        {
            for(int j=0;j<outW;j++)
            {
                for(int m=0;m<kSizeY;m++)
                {
                    for(int n=0;n<kSizeX;n++)
                    {
                        float fVal = 0;
                        if((n+j*strideX-padX)>-1&&(m+i*strideY-padY>-1)&&(n+j*strideX-padX)<=width&&(m+i*strideY-padY>-1)<=height)
                        {
                            fVal = F[c*width*height + (m+i*strideY-padX)*width+(n+j*strideX-padY)];
                        }
                        O[i*outW+j]+=K[c*kSizeX*kSizeY+m*kSizeX+n]*fVal;
                    }
                }
            }
        }
    }

    for (int i = 0; i < outH; ++i)
    {
        for (int j = 0; j < outW; ++j)
        {
            std::cout<<O[i*outW+j]<<" ";
        }
        std::cout<<std::endl;
    }
}

void demo5()
{

    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    //float K[] = {1,2,3,4};
    float K[] = {1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9,
                 1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9
                };
    float O[] = {0,0,0,0,0,0,0,0};

    int padX = 1;
    int padY = 1;

    int dilationX = 1;
    int dilationY = 1;

    int strideX  = 2;
    int strideY  = 2;

    int width = 4;
    int height = 4;

    int kSizeX = 3;
    int kSizeY = 3;

    int channel = 2;

    int filters = 2;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    int outC = filters;

    for (int oc = 0; oc < outC; ++oc)
    {
        for (int c = 0; c < channel; ++c)
        {
            for(int i=0;i<outH;i++)
            {
                for(int j=0;j<outW;j++)
                {
                    for(int m=0;m<kSizeY;m++)
                    {
                        for(int n=0;n<kSizeX;n++)
                        {
                            float fVal = 0;
                            if((n+j*strideX-padX)>-1&&(m+i*strideY-padY>-1)&&(n+j*strideX-padX)<=width&&(m+i*strideY-padY>-1)<=height)
                            {
                                fVal = F[c*width*height + (m+i*strideY-padX)*width+(n+j*strideX-padY)];
                            }
                            O[oc*outH*outW+i*outW+j]+=K[oc*channel*kSizeX*kSizeY+c*kSizeX*kSizeY+m*kSizeX+n]*fVal;
                        }
                    }
                }
            }
        }
    }

    for (int oc = 0; oc < outC; ++oc)
    {
        for (int i = 0; i < outH; ++i)
        {
            for (int j = 0; j < outW; ++j)
            {
                std::cout<<O[oc*outH*outW+i*outW+j]<<" ";
            }
            std::cout<<std::endl;
        }
        std::cout<<std::endl<<std::endl;
    }
}

void demo6()
{
    // (height + 2 * paddingY - (dilationY * (kSizeY - 1) + 1)) / strideY + 1;
    // (width + 2 * paddingX - (dilationX * (kSizeX - 1) + 1)) / strideX + 1;

    float F[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};
    //float K[] = {1,2,3,4};
    float K[] = {1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9,
                 1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9
                };
    float O[] = {0,0,0,0,0,0,0,0};

    int padX = 1;
    int padY = 1;

    int dilationX = 2;
    int dilationY = 2;

    int strideX  = 1;
    int strideY  = 1;

    int width = 4;
    int height = 4;

    int kSizeX = 3;
    int kSizeY = 3;

    int channel = 2;

    int filters = 2;

    int outH = (height+2*padY-(dilationY*(kSizeY-1)+1)) / strideY + 1;
    int outW = (width+2*padX-(dilationX*(kSizeX-1)+1)) / strideX + 1;

    int outC = filters;

    for (int oc = 0; oc < outC; ++oc)
    {
        for (int c = 0; c < channel; ++c)
        {
            for(int i=0;i<outH;i++)
            {
                for(int j=0;j<outW;j++)
                {
                    for(int m=0;m<kSizeY;m++)
                    {
                        for(int n=0;n<kSizeX;n++)
                        {
                            float fVal = 0;
                            if( ((n+j*strideX)*dilationX-padX)>-1 && ((m+i*strideY)*dilationY-padY)>-1&&
                                    ((n+j*strideX)*dilationX-padX)<=width && ((m+i*strideY)*dilationY-padY>-1)<=height)
                            {
                                fVal = F[c*width*height + ((m+i*strideY)*dilationX-padX)*width+((n+j*strideX)*dilationY-padY)];
                            }
                            O[oc*outH*outW+i*outW+j]+=K[oc*channel*kSizeX*kSizeY+c*kSizeX*kSizeY+m*kSizeX+n]*fVal;
                        }
                    }
                }
            }
        }
    }

    for (int oc = 0; oc < outC; ++oc)
    {
        for (int i = 0; i < outH; ++i)
        {
            for (int j = 0; j < outW; ++j)
            {
                std::cout<<O[oc*outH*outW+i*outW+j]<<" ";
            }
            std::cout<<std::endl;
        }
        std::cout<<std::endl;
    }
}


int main(int argc, char *argv[])
{
    //demo0();
    demo1();
    //demo2();
    //demo3();
    //demo4();
    //demo5();
    //demo6();
}

（1）将上述文件为my_code.cc源文件。

如果要使用不同类型的demo，可以直接在main函数中调用。

（2）然后在终端运行：

g++ -o my_code my_code.cc

此时已编译出可执行的二进制my_code。

（3）执行my_code文件

./my_code

最后说明：其实我个人觉得这种方式使用起来除了简单易懂，但在实际操作中并不可取。主要是所有的变量值都需要在demo()函数中手工赋值，耦合性和实用性较差。但是目前也没有更好的实测，等过阵子我的程序写完后，再和大家分享。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1826496.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何避免销售飞单私单！教你如何巧妙避开陷阱，业绩飙升！

如何避免销售飞单私单！教你如何巧妙避开陷阱，业绩飙升！

明明投入了大量的时间和精力&#xff0c;客户却悄无声息地消失了&#xff1f;或是突然有一天&#xff0c;你发现原本属于你的订单被同事悄悄抢走&#xff1f;这背后&#xff0c;很可能隐藏着销售飞单私单的陷阱。今天&#xff0c;就让我们一起探讨如何巧妙避开这些陷阱&#xf…
阅读更多...
MySQL-----InnoDB的自适应哈希索引

MySQL-----InnoDB的自适应哈希索引

InnoDB存储引擎监测到同样的二级索引不断被使用&#xff0c;那么它会根据这个二级索引&#xff0c;在内存上根据二级索引树(B树)上的二级索引值&#xff0c;在内存上构建一个哈希索引&#xff0c;来加速搜索。 查看是否开启自适应哈希索引 show variables like innodb_adapti…
阅读更多...
2024年【安全生产监管人员】试题及解析及安全生产监管人员考试试题

2024年【安全生产监管人员】试题及解析及安全生产监管人员考试试题

题库来源&#xff1a;安全生产模拟考试一点通公众号小程序 安全生产监管人员试题及解析是安全生产模拟考试一点通总题库中生成的一套安全生产监管人员考试试题&#xff0c;安全生产模拟考试一点通上安全生产监管人员作业手机同步练习。2024年【安全生产监管人员】试题及解析及…
阅读更多...
LLM资料大全：文本多模态大模型、垂直领域微调模型、STF数据集、训练微调部署框架、提示词工程等

LLM资料大全：文本多模态大模型、垂直领域微调模型、STF数据集、训练微调部署框架、提示词工程等

前言 自ChatGPT为代表的大语言模型&#xff08;Large Language Model, LLM&#xff09;出现以后&#xff0c;由于其惊人的类通用人工智能&#xff08;AGI&#xff09;的能力&#xff0c;掀起了新一轮[自然语言处理]领域的研究和应用的浪潮。尤其是以ChatGLM、LLaMA等平民玩家都…
阅读更多...
Qwen-Agent：Qwen2加持，强大的多代理框架 - 函数调用、代码解释器以及 RAG！

Qwen-Agent：Qwen2加持，强大的多代理框架 - 函数调用、代码解释器以及 RAG！

✨点击这里✨&#xff1a;&#x1f680;原文链接&#xff1a;&#xff08;更好排版、视频播放、社群交流、最新AI开源项目、AI工具分享都在这个公众号&#xff01;&#xff09; Qwen-Agent&#xff1a;Qwen2加持&#xff0c;强大的多代理框架 - 函数调用、代码解释器以及 RAG&…
阅读更多...
全局解决SpringBoot框架中的application.properties/yml注解中文乱码问题（一劳永逸）

全局解决SpringBoot框架中的application.properties/yml注解中文乱码问题（一劳永逸）

问题原因 Spring Boot在加载application.properties/yml配置文件时&#xff0c;默认使用ISO-8859-1编码。这种编码方式并不支持中文字符&#xff0c;因此当配置文件中包含中文字符时&#xff0c;就会出现乱码&#xff0c;现象如下&#xff1a; 问题解决 本解决方法是全局设置…
阅读更多...
最快安装zabbix

最快安装zabbix

部署zabbix 6.x 建议使用红帽系统。 https://download.rockylinux.org/pub/rocky/8/isos/x86_64/Rocky-8.9-x86_64-minimal.iso1> 配置安装yum源 [rootzabbix ~]# yum install https://mirrors.huaweicloud.com/zabbix/zabbix/6.2/rhel/8/x86_64/zabbix-release-6.2-3.el8…
阅读更多...
PMS助力制造企业高效运营︱PMO大会

PMS助力制造企业高效运营︱PMO大会

全国PMO专业人士年度盛会 北京易贝恩项目管理科技有限公司副总经理朱洪泽女士受邀为PMO评论主办的2024第十三届中国PMO大会演讲嘉宾&#xff0c;演讲议题为“PMS助力制造企业高效运营”。大会将于6月29-30日在北京举办&#xff0c;敬请关注&#xff01; 议题简要&#xff1a; …
阅读更多...
DeepDriving | CUDA编程-05：流和事件

DeepDriving | CUDA编程-05：流和事件

本文来源公众号“DeepDriving”&#xff0c;仅用于学术分享&#xff0c;侵权删&#xff0c;干货满满。 原文链接&#xff1a;CUDA编程-05&#xff1a;流和事件 1 CUDA流 在CUDA中有两个级别的并发&#xff1a;内核级并发和网格级并发。前面的文章DeepDriving | CUDA编程-04&…
阅读更多...
基于System-Verilog点亮LED灯

基于System-Verilog点亮LED灯

文章目录 一、System-Verilog介绍1.1System-Verilog 二、简单的语法介绍2.1接口实例2.2全局声明和语句实例2.3时间单位和精度2.4用户定义的类型2.5 枚举类型 三、流水灯参考 一、System-Verilog介绍 1.1System-Verilog SystemVerilog是一种硬件描述和验证语言&#xff08;HDV…
阅读更多...
数据分析必备：一步步教你如何用matplotlib做数据可视化（2）

数据分析必备：一步步教你如何用matplotlib做数据可视化（2）

1、Matplotlib Anaconda Anaconda是Python和R编程语言的免费开源发行版&#xff0c;用于大规模数据处理&#xff0c;预测分析和科学计算。 该分发使包管理和部署变得简单容易。 Matplotlib和许多其他有用的(数据)科学工具构成了分发的一部分。 包版本由包管理系统Conda管理。 …
阅读更多...
50【Aseprite 作图】模糊工具 笔刷

50【Aseprite 作图】模糊工具 笔刷

1 模糊工具 2 笔刷 然后 选中 后 Ctrl B&#xff0c;就变成笔刷了 可以按住shift &#xff0c;像画一条线一样 或者用矩形、圆形工具、油漆桶工具 在上方可以选择笔刷的不同形式&#xff0c;如果是“图案与来源对齐”&#xff0c;就是来源不变&#xff0c;笔刷不会覆盖之前…
阅读更多...
Vue3【十五】标签的Ref属性

Vue3【十五】标签的Ref属性

Vue3【十五】标签的Ref属性 标签的ref属性 用于注册模板引用 用在dom标签上&#xff0c;获取的是dom节点 用在组件上&#xff0c;获取的是组件实例对象 案例截图 目录结构 代码 app.vue <template><div class"app"><h1 ref"title2">你…
阅读更多...
uniapp开发微信小程序问题汇总

uniapp开发微信小程序问题汇总

1. 自定义校验规则validateFunction失效 2. 微信小程序不支持<Br>换行 在 <text></text> 标签中使用\n(必须 text 标签&#xff0c;view 标签无效 ) 3. 微信小程序无法使用本地静态资源图片的解决方法 (1) 将图片上传到服务器&#xff0c;小程序访问该图片…
阅读更多...
sql优化之利用聚簇索引减少回表次数：limit 100000,10

sql优化之利用聚簇索引减少回表次数：limit 100000,10

1. 问题描述 产品&#xff1a;我要对订单列表页做一个分页功能&#xff0c;每页10条数据&#xff0c;商家可以根据金额过滤订单 技术&#xff1a;好的&#xff0c;我写一个sql实现分页&#xff0c;x表示偏移页数&#xff0c;自测limit 10,10耗时200ms&#xff1a; SELECT * …
阅读更多...
C# WPF入门学习主线篇（二十三）—— 控件模板（ControlTemplate）和数据模板（DataTemplate）

C# WPF入门学习主线篇（二十三）—— 控件模板（ControlTemplate）和数据模板（DataTemplate）

C# WPF入门学习主线篇&#xff08;二十三&#xff09;—— 控件模板&#xff08;ControlTemplate&#xff09;和数据模板&#xff08;DataTemplate&#xff09; 在WPF开发中&#xff0c;控件模板&#xff08;ControlTemplate&#xff09;和数据模板&#xff08;DataTemplate&am…
阅读更多...
Opencv基本操作

Opencv基本操作

Opencv基本操作 导入并使用opencv进行图像与视频的基本处理 opencv读取的格式是BGR import cv2 #opencv读取的格式是BGR import numpy import matplotlib.pyplot as plt %matplotlib inline图像读取 通过cv2.imread()来加载指定位置的图像信息。 img cv2.imread(./res/ca…
阅读更多...
Tomcat基础详解

Tomcat基础详解

第一篇&#xff1a;Tomcat基础篇 lecture&#xff1a;邓澎波 一、构建Tomcat源码环境 工欲善其事必先利其器&#xff0c;为了学好Tomcat源码&#xff0c;我们需要先在本地构建一个Tomcat的运行环境。 1.源码环境下载 源码有两种下载方式&#xff1a; 1.1 官网下载 https://…
阅读更多...
联想正式发布全栈算力基础设施新品，加速筑基AI 2.0时代

联想正式发布全栈算力基础设施新品，加速筑基AI 2.0时代

6月14日&#xff0c;以“异构智算 稳定高效”为主题的联想算力基础设施新品发布会在北京成功举办。 据「TMT星球」了解&#xff0c;在与会嘉宾和合作伙伴的见证下&#xff0c;联想正式发布率先搭载英特尔至强 6能效核处理器的联想问天WR5220 G5、联想ThinkSystem SR630 V4、联…
阅读更多...
Qt项目天气预报(2) - 重写事件函数

Qt项目天气预报(2) - 重写事件函数

鼠标右键实现退出界面 知识点QMenu: QMenu 弹出对话框 --> 相对QMessageBox 更加轻量点 QMenu是Qt库中用于创建弹出式菜单的类&#xff0c;它通常出现在应用程序的顶部菜单栏、按钮的右键菜单或自定义上下文菜单中。以下是关于QMenu的详细介绍&#xff1a; 1. 类的基本特…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023