1.目标-数出有多少个贴纸

好久没更新博客了，最近家里小朋友在一张A3纸上贴了很多水晶贴纸，要让我帮他数有多少个，看上去有点多，贴的也比较随意，于是想着使用Opencv来识别一下有多少个。

原图如下： 

代码：

import cv2
import numpy as np
from matplotlib import pyplot as plt


def count_stars(image_path):
    # 读取图像
    image = cv2.imread(image_path)

    # # 显示原始图像
    # plt.figure()
    # plt.imshow(cv2.cvtColor(image, cv2.COLOR_BGR2RGB))
    # plt.title('Original Image')

    # 转换为灰度图像
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

    # # 显示灰度图像
    # plt.figure()
    # plt.imshow(gray, cmap='gray')
    # plt.title('Gray Image')

    # 应用高斯模糊以减少噪声
    gs=85
    blurred = cv2.GaussianBlur(gray, (gs, gs), 0)

    # # 显示高斯模糊后的图像
    # plt.figure()
    # plt.imshow(blurred, cmap='gray')
    # plt.title('Blurred Image')
    # # plt.show()

    # 使用自适应阈值进行二值化
    binary = cv2.adaptiveThreshold(blurred, 255,
                                   cv2.ADAPTIVE_THRESH_MEAN_C,
                                   cv2.THRESH_BINARY_INV, 125, 2)

    # 显示二值化后的图像
    plt.figure()
    plt.imshow(binary, cmap='gray')
    plt.title('Binary Image')
    plt.show()

    # 查找轮廓
    contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL,
                                   cv2.CHAIN_APPROX_SIMPLE)

    # 绘制轮廓
    contour_image = np.copy(image)
    cv2.drawContours(contour_image, contours, -1, (0, 255, 0), 3)

    # 计数星星（即轮廓的数量）
    star_count = len(contours)
    # 显示带有轮廓的图像
    plt.figure()
    plt.imshow(cv2.cvtColor(contour_image, cv2.COLOR_BGR2RGB))
    plt.title('Image with Contours'+str(star_count))
    plt.show()

    return star_count

# 图像路径
image_path = '202406150928253.jpg'

# 计算星星数量
num_stars = count_stars(image_path)
print(f'Number of stars: {num_stars}')

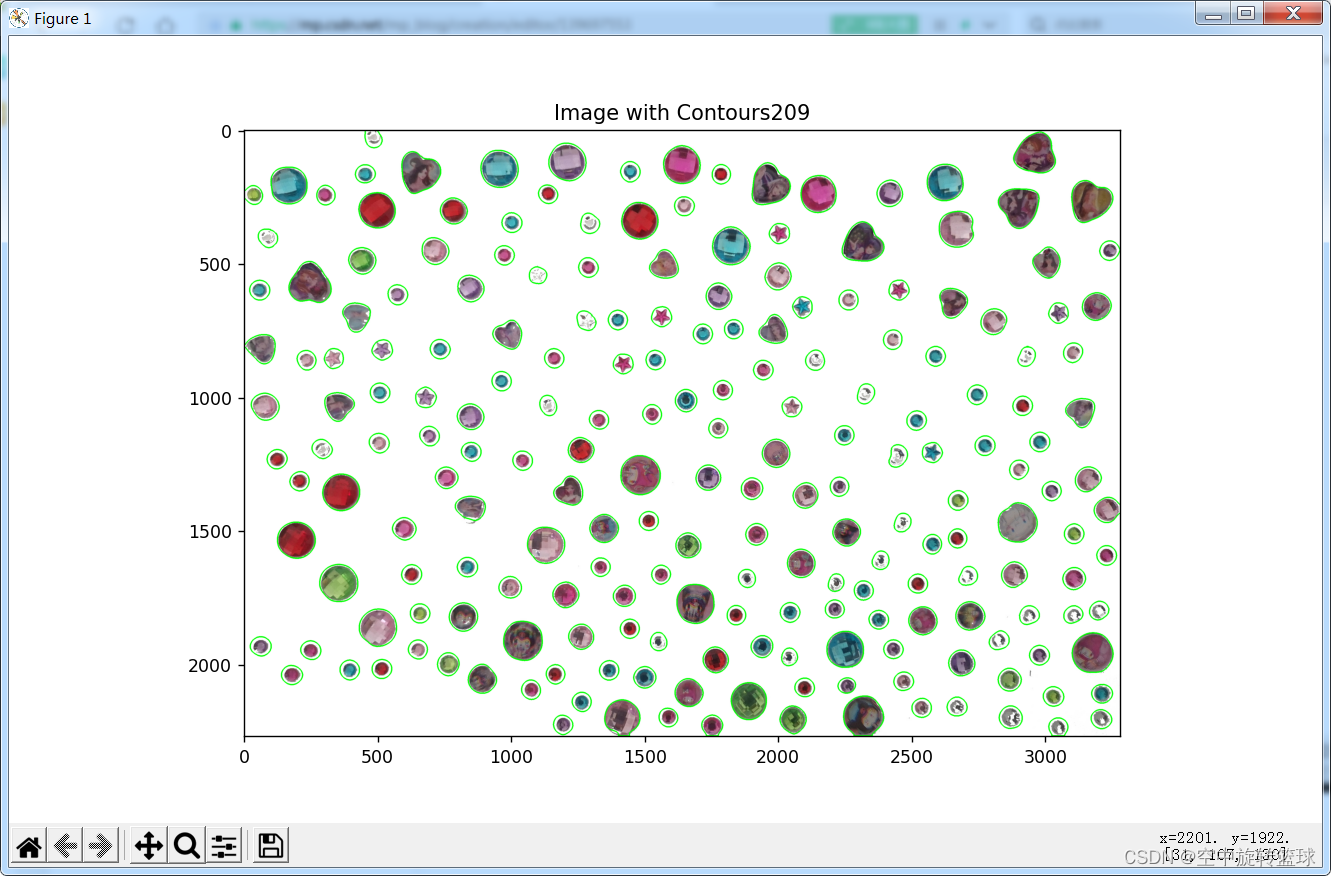
2.使用原图计算效果

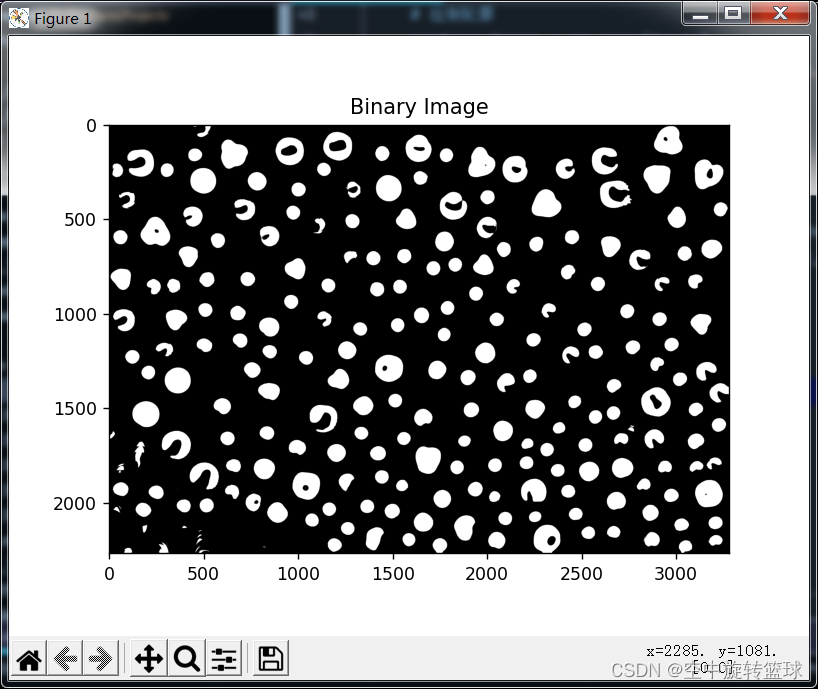
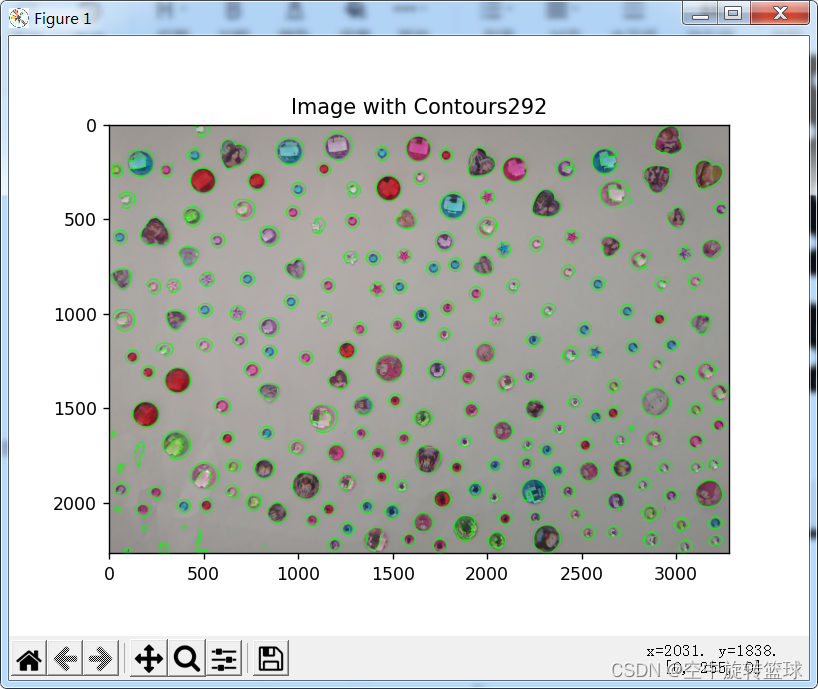
有很多斑点干扰了统计结果。

3.图像优化处理

对图像进行优化处理再进行计算。使用PS工具对图像背景进行去除。

PS处理之后的图（魔术橡皮擦擦掉背景）），有些透明水晶贴纸和背景色接近被处理了一部分。

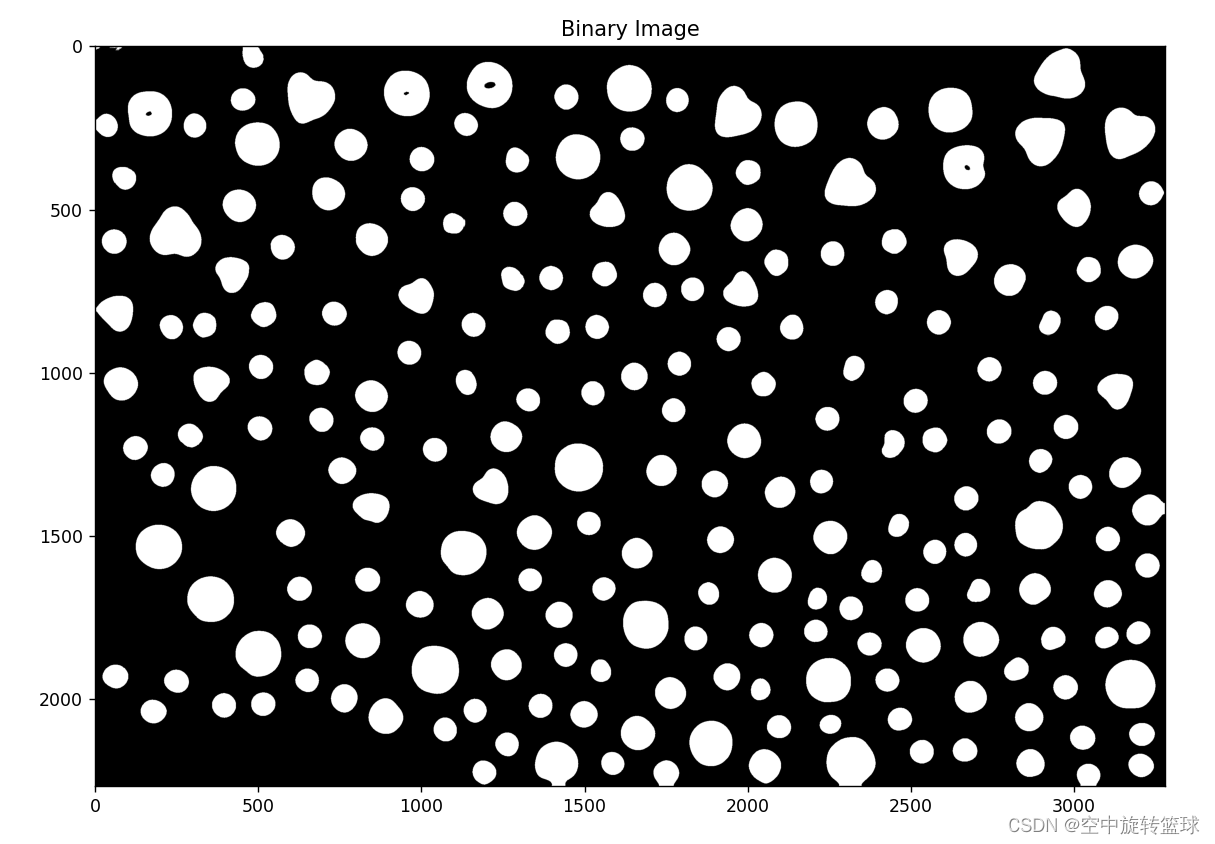
最后的结果没有进行人工确认，不过看上去基本是正确的。有兴趣的朋友可以比对一下。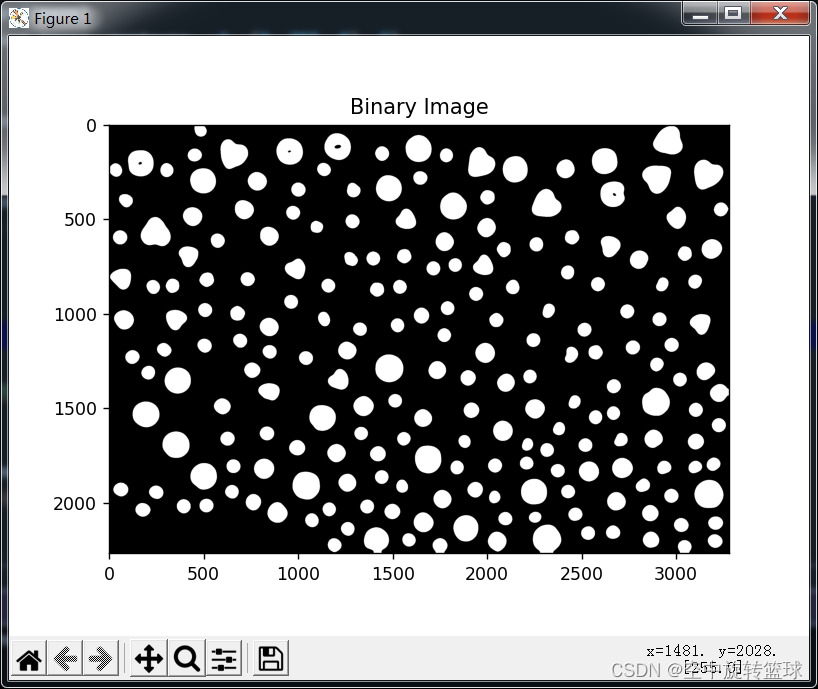

仔细看左上角有点问题，多了一些，擦除后重新计算得到209个，家里小朋友数的202个。