秋招突击——6/14——复习{（树形DP）树的最长路径}——新作{非递归求二叉树的深度、重复区间合并}

文章目录

- 引言
- 复习
- - 树形DP——树的最长路径
- 新作
- - 使用dfs非递归计算二叉树的深度
  - 多个区间合并删除问题
  - - 实现思路
    - 实现代码
    - 参考思路
- 总结

引言

这两天可能有点波动，但是算法题还是尽量保证复习和新作一块弄，数量上可能有所差别。

复习

树形DP——树的最长路径

这道题是没有完全听完，但是到现在这个阶段，最起码得数组实现邻接链表做完。

无向图的一维数组表示邻接表实现

首先说明一下，这里要使用邻接链表实现，这里是使用一维数组实现的邻接链表。
同时这里是双向链表，所以，要加两次边，具体是实现如下

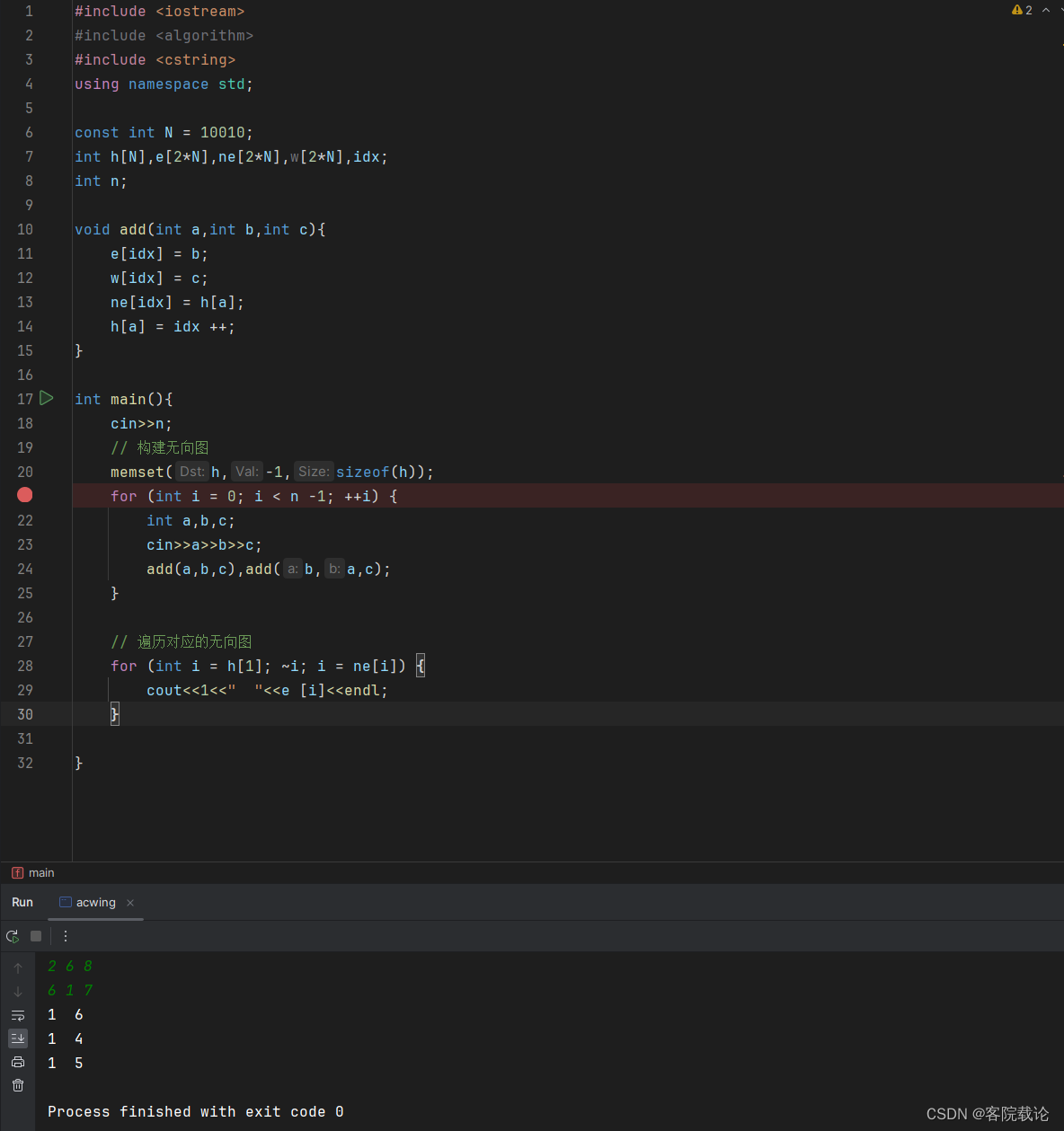
在这里插入图片描述

下面开始具体的分析

树是一个确定的拓扑结构，每一个节点之间是是存在对应的父子关系，所以列觉路径可以更换为枚举中间节点，具体分析见下图，这是参考别人的，分析的很有道理
通过红色节点的有三条路径
- 红色路径，是一红色节点为根节点的最长的路径
- 蓝色路径，是以红色节点为跟节点的最长路径和次长路径的和
- 橙色路径，是红色节点的父节点的相同情况，具体见上图。
相当于这道题，就是在遍历的过程中，计算对应的最长路径和子路径，然后在计算两者的和。

图片参考来源
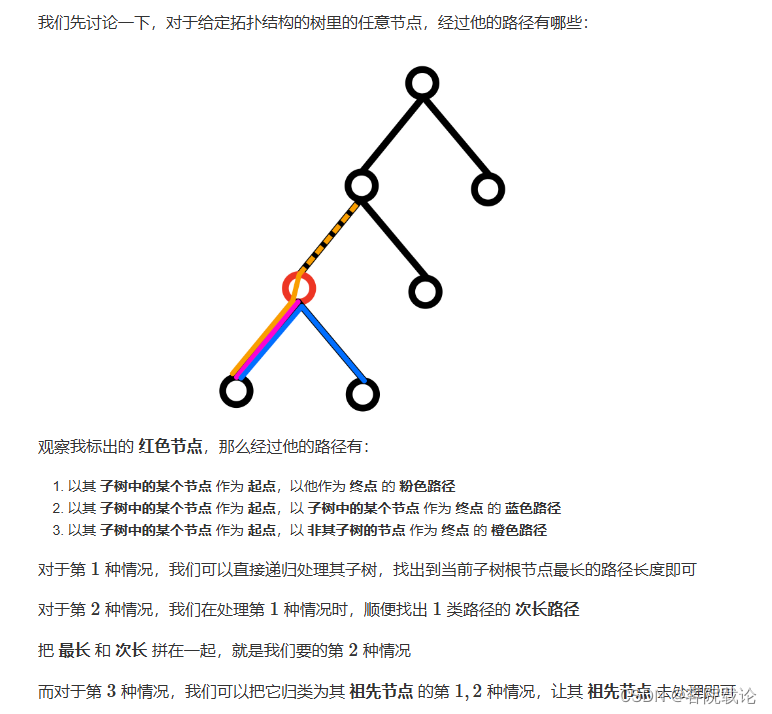
在这里插入图片描述

动态规划分析

这道题是两个动态规划，分别是动态规划计算最长的路径，次长的路径，而且是一个很明显的动态规划题目，就是子状态影响最终的状态。
所以状态转移函数，就是计算的最长路径和次长路径，这里的动态规划，就是两个路径，f1[i]表示以节点i为根节点的最长路径，f2[i]表示以i为根节点的次长路径。具体如下

在这里插入图片描述

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 10010;
int h[N],e[2*N],ne[2*N],w[2*N],idx;
int f1[N],f2[N],res; // f1保存最长的转移路径，f2保存次长的转移路径
int n;

void add(int a,int b,int c){
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx ++;
}

void dfs(int r,int father){
    // 这里r是对应的根节点，father是对应的父节点
    f1[r] = 0,f2[r] = 0;
    for (int i = h[r]; ~i; i = ne[i]) {
        int j = e[i];  // 确定子节点的编号
        if (j == father)    continue;
        dfs(j,r);
        if(f1[j] + w[i] >= f1[r]) f2[r] = f1[r],f1[r] = f1[j] + w[i];
        else if(f1[j] + w[i] > f2[r]) f2[r] = f1[j] + w[i];
    }
    res = max(res,f1[r] + f2[r]);
}

int main(){
    cin>>n;
    // 构建无向图
    memset(h,-1,sizeof(h));
    for (int i = 0; i < n -1; ++i) {
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c),add(b,a,c);
    }

    // 遍历对应的无向图
    for (int i = h[1]; ~i; i = ne[i]) {
        cout<<1<<"  "<<e [i]<<endl;
    }

    cout<<res;
    return 0;
}

这道题拖了那么久，乍一看，其实还是蛮简单的，思路只要清楚了，后续还是很好实现的，然后那个使用一维数组实现的邻接链表的，之前是没有做过，现在知道怎么用了，还是蛮简单的。

新作

使用dfs非递归计算二叉树的深度

dfs非递归二叉树高度，一开始写了个经典队列的bfs，意识到不对后开始改，最后没改完，就说了个暴力找到每个叶子的高度的思路。
这个忘记的有点多，如果单纯使用栈来实现的话，就需要每一次入栈当前节点的子节点还有对应的深度，然后出栈，如果是叶子节点，就比较一下长度，如果不是，就继续做出栈和入栈的操作。
这里实现的基本上和我写的比较类似

#include <iostream>
#include <stack>

using namespace std;

struct TreeNode{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x):val(x),left(NULL),right(NULL){};
};

// 生成样例
TreeNode* createSampleTree1() {
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    root->right->right = new TreeNode(6);
    root->left->left->left = new TreeNode(7);
    return root;
}

int treeHeight(TreeNode* root){
    // 使用非递归的方式计算的树深度
    stack<pair<TreeNode *,int>> s;

    // 根节点入栈并重置深度
    s.push({root,1});
    int r = 0;
    // 出栈并遍历每一个节点的子节点
    while(!s.empty()){
        TreeNode* t = s.top().first;
        int l = s.top().second;
        s.pop();

        // 判定左子节点是否为空
        if (t->left)    s.push({t->left,l + 1});
        if (t->right)    s.push({t->right,l + 1});

        // 比较深度
        r = max(r,l);
    }
    return r;
}

int main(){
    TreeNode* root = createSampleTree1();
    cout<<treeHeight(root);
}

参考方法
- 这里指的学习的是一个auto的使用，通过下述方式可以直接进行遍历使用。

auto [node, depth] = stack.top();

#include <iostream>
#include <stack>
#include <algorithm> // for max

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

int treeHeight(TreeNode* root) {
    if (root == nullptr) return 0;

    std::stack<std::pair<TreeNode*, int>> stack;
    stack.push({root, 1});
    int maxHeight = 0;

    while (!stack.empty()) {
        auto [node, depth] = stack.top();
        stack.pop();
        if (node != nullptr) {
            maxHeight = std::max(maxHeight, depth);
            if (node->left != nullptr) stack.push({node->left, depth + 1});
            if (node->right != nullptr) stack.push({node->right, depth + 1});
        }
    }

    return maxHeight;
}

int main() {
    // 示例二叉树
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);

    std::cout << "树的高度是: " << treeHeight(root) << std::endl;

    // 清理内存
    delete root->left->left;
    delete root->left->right;
    delete root->left;
    delete root->right;
    delete root;

    return 0;
}

多个区间合并删除问题

这个也是在网上搜索的，部分拼多多主管面可能问到的题目，所以这里做一下，具体题目描述如下

给定一个n×2的二维数组，数组的每一行代表一个区间，
如果一个区间被另一个区间包含就删掉该区间，返回剩
下的所有区间。
* 比如: [1 2]被[1 ,3]包含。

实现思路

这里是使用自定义排序实现的，如果包含关系，就将之按照包含的关系进行排序，然后在进行从前往后逐步进行遍历，对于相同的数组直接去除。最后剩下的就是对应的元素。
自定义排序实现贪婪算法！
这个方法确实是有问题的，有一部分样例是没有考虑到，不过背一下这个模版的。

实现代码

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

using Interval = pair<int,int>;

vector<Interval> removeContainedIntervals(vector<Interval>& intervals){

    // 可以对区间进行排序，按照包含关系进行排序
    vector<Interval> res;
    sort(intervals.begin(),intervals.end(),[](auto a,auto b){
        if(a.first <= b.first && a.second >= b.second)    return 1;
        else return 0;
    });
    for (int i = 0;i < intervals.size();i ++) {
        Interval t = intervals[i];
        res.push_back(t);
        while((i + 1 < intervals.size())
            && t.first <= intervals[i+1].first
            && t.second >= intervals[i+1].second)
            i ++;

    }
    return res;
}

int main() {
    vector<vector<Interval>> samples = {
            {{1, 4}, {2, 3}, {1, 3}, {4, 6}, {5, 7}},
//            {{1, 5}, {2, 4}, {6, 8}, {7, 9}, {5, 10}},
//            {{1, 2}, {3, 4}, {2, 3}, {1, 5}, {6, 7}},
//            {{1, 2}, {2, 3}, {3, 4}, {4, 5}},
//            {{1, 3}, {2, 6}, {8, 10}, {15, 18}}
    };

    for (size_t i = 0; i < samples.size(); ++i) {
        vector<Interval> result = removeContainedIntervals(samples[i]);
        cout << "样例 " << i + 1 << " 剩余的区间为：" << endl;
        for (const auto& interval : result) {
            cout << "[" << interval.first << ", " << interval.second << "] ";
        }
        cout << endl;
    }

    return 0;
}

参考思路

这里是一个贪心算法解决区间问题的模板，需要好好练习一下，和我的方法差不多，只不过他是针对单边进行排序的
这里是使用标准区间进行比较的，会更加灵活方便一点，比我的方法要好很多。

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// 定义一个区间类型
using Interval = pair<int, int>;

// 比较函数，用于排序区间
bool compareIntervals(const Interval &a, const Interval &b) {
    if (a.first == b.first) {
        return a.second < b.second;
    }
    return a.first < b.first;
}

vector<Interval> removeContainedIntervals(vector<Interval>& intervals) {
    // 如果区间列表为空，直接返回空列表
    if (intervals.empty()) {
        return {};
    }

    // 按照起始点排序，起始点相同则按照终止点排序
    sort(intervals.begin(), intervals.end(), compareIntervals);

    vector<Interval> result;
    Interval last = intervals[0]; // 初始化第一个区间作为比较基准

    for (size_t i = 1; i < intervals.size(); ++i) {
        // 如果当前区间不被上一个区间包含
        if (intervals[i].first > last.first && intervals[i].second > last.second) {
            result.push_back(last); // 保留上一个区间
            last = intervals[i];    // 更新比较基准
        } else {
            // 如果当前区间的终止点更长，更新比较基准
            if (intervals[i].second > last.second) {
                last = intervals[i];
            }
        }
    }

    // 最后一个区间也需要保留
    result.push_back(last);

    return result;
}

int main() {
    vector<vector<Interval>> samples = {
        {{1, 4}, {2, 3}, {1, 3}, {4, 6}, {5, 7}},
        {{1, 5}, {2, 4}, {6, 8}, {7, 9}, {5, 10}},
        {{1, 2}, {3, 4}, {2, 3}, {1, 5}, {6, 7}},
        {{1, 2}, {2, 3}, {3, 4}, {4, 5}},
        {{1, 3}, {2, 6}, {8, 10}, {15, 18}}
    };

    for (size_t i = 0; i < samples.size(); ++i) {
        vector<Interval> result = removeContainedIntervals(samples[i]);
        cout << "样例 " << i + 1 << " 剩余的区间为：" << endl;
        for (const auto& interval : result) {
            cout << "[" << interval.first << ", " << interval.second << "] ";
        }
        cout << endl;
    }

    return 0;
}