1、实验设备

PC计算机1台，MATLAB软件1套。

2、实验目的：

1. 学习使用离散傅里叶变换（DFT）进行信号谱分析的方法。
2. 选择合适的变换区间长度N，对给定信号进行谱分析，并绘制幅频特性和相频曲线。

3、实验原理说明：

1. 离散傅里叶变换（DFT）是一种将离散信号从时域转换到频域的方法，可用于分析信号的频谱。
2. 幅频特性表示信号在频率域上的幅度分布，相频曲线表示信号在频率域上的相位分布。

4、实验步骤：

1. 对给定的信号X1 (n) = 2cos(0.2πn)  X2(n)= sin(0.45πn)sin(0.55πn)  X3 (n)=2-|n|R21(n+10)分别选择合适的变换区间长度N。
2. 使用MATLAB编程实现DFT，计算并绘制每个信号的幅频特性和相频曲线。
3. 在MATLAB界面下调试程序，确保程序运行正确，并查看绘制的谱分析图。

注意：在实验中，可以使用MATLAB的`fft`函数进行DFT计算，并使用`abs`和`angle`函数获取幅度和相位信息。绘制图形可以使用`plot`函数。通过观察图形，分析信号在频域上的特性。

题目：27).选择合适的变换区间长度N，用DFT对下列信号进行谱分析，画出幅频特性和相频曲线。

X1 (n) = 2cos(0.2πn)

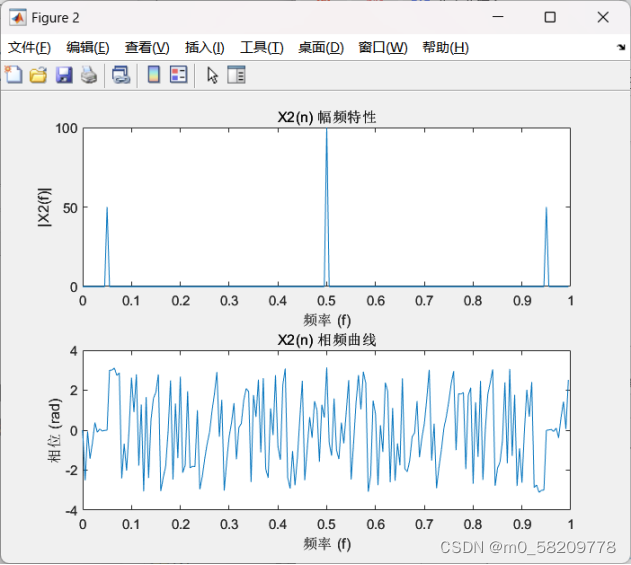
X2(n)= sin(0.45πn)sin(0.55πn)

X3 (n)=2-|n|R21(n+10)

% 信号 X1(n) = 2cos(0.2πn)
n1 = 0:99;
X1 = 2 * cos(0.2 * pi * n1);
N1 = length(X1);

% 计算DFT
X1_fft = fft(X1, N1);

% 计算频率轴
f1 = (0:N1-1) / N1;

% 绘制幅频特性图
figure;
subplot(2, 1, 1);
plot(f1, abs(X1_fft));
title('X1(n) 幅频特性');
xlabel('频率 (f)');
ylabel('|X1(f)|');

% 绘制相频曲线
subplot(2, 1, 2);
plot(f1, angle(X1_fft));
title('X1(n) 相频曲线');
xlabel('频率 (f)');
ylabel('相位 (rad)');

% 信号 X2(n) = sin(0.45πn)sin(0.55πn)
n2 = 0:199;
X2 = sin(0.45 * pi * n2) .* sin(0.55 * pi * n2);
N2 = length(X2);

% 计算DFT
X2_fft = fft(X2, N2);

% 计算频率轴
f2 = (0:N2-1) / N2;

% 绘制幅频特性图
figure;
subplot(2, 1, 1);
plot(f2, abs(X2_fft));
title('X2(n) 幅频特性');
xlabel('频率 (f)');
ylabel('|X2(f)|');

% 绘制相频曲线
subplot(2, 1, 2);
plot(f2, angle(X2_fft));
title('X2(n) 相频曲线');
xlabel('频率 (f)');
ylabel('相位 (rad)');

% 信号 X3(n) = 2^(-|n|) R21(n+10)
n3 = -10:89;
X3 = 2.^(-abs(n3)) .* (n3 >= -10);
N3 = length(X3);

% 计算DFT
X3_fft = fft(X3, N3);

% 计算频率轴
f3 = (0:N3-1) / N3;

% 绘制幅频特性图
figure;
subplot(2, 1, 1);
plot(f3, abs(X3_fft));
title('X3(n) 幅频特性');
xlabel('频率 (f)');
ylabel('|X3(f)|');

% 绘制相频曲线
subplot(2, 1, 2);
plot(f3, angle(X3_fft));
title('X3(n) 相频曲线');
xlabel('频率 (f)');
ylabel('相位 (rad)');