电子技术——MOS放大器基础

我们已经学过MOS可以当做一个压控流源，使用栅极电压 $v_{GS}$ 控制漏极电流 $i_D$ 。尽管两个量的关系不是线性的，稍后我们将会介绍偏置在线性区的工作方法。

构建压控压源放大器

现在，我们有了一个压控流源，将电流线性转换为电压只需要将电流通过一个电阻，然后测量电阻电压即可。

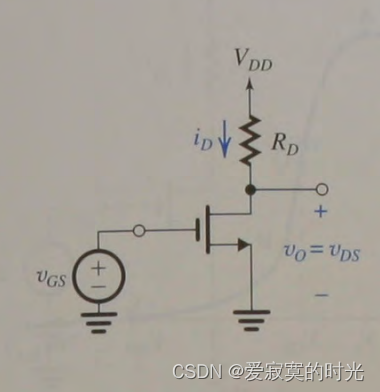
如上图，电阻 $R_D$ （称为负载电阻）通过栅极电流，输出电压：

$$v_O=v_{DS}=V_{DD}-i_D{R}_D$$

电压传导特性曲线

根据上面的关系式，我们构建起 $v_O$ 和 $v_{GS}$ 之间的传导特性关系曲线：

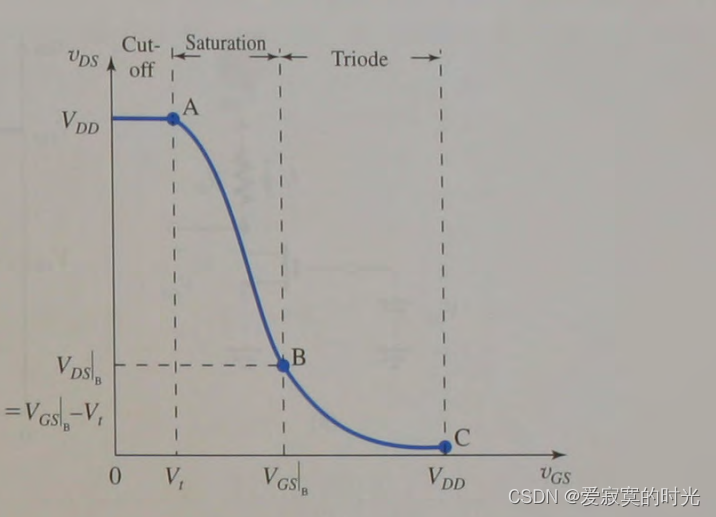
注意到，当 $v_{GS}<V_t$ 的时候，MOS管处于截止区，此时栅极无电流通过，输出电压即为 $V_{DD}$ 。当 $v_{GS}$ 继续增大，MOS管进入饱和区，输出电压持续减小，当达到临界点 $B$ 点时，MOS管进入三极管区，输出电压迅速减小。

关于放大器，我们只关心饱和区的特性关系，即 AB 曲线。由上节给出的饱和电流，我们可以构建输入输出电压的最终关系式：

$$v_{DS}=V_{DD}-\frac{1}{2}{k}_n{R}_D(v_{GS}-V_t{)}^2$$

这显然是一个非线性关系，但是我们可以通过偏置方法来获得线性工作。在那之前，我们希望计算出 B 点的坐标。我们令 $v_{DS}=v_{GS}-V_t$ 带入上面的方程得到：

$$V_{GS}{|}_B=V_t+\frac{\sqrt{2k_n{R}_D{V}_{DD}+1}-1}{k_n{R}_D}$$

使用偏置获得线性工作区

首先我们先通过设置一个合理的DC $V_{GS}$ 和 $V_{DD}$ 电压，如下图：

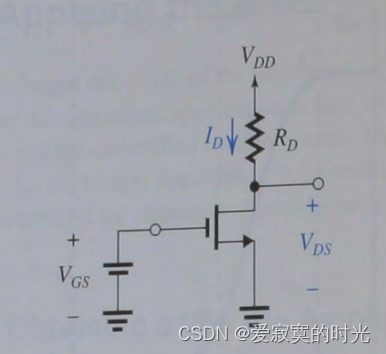
根据电压传导方程，这将唯一决定一个 $V_{DS}$ 值，即为：

$$V_{DS}=V_{DD}-\frac{1}{2}{k}_n{R}_D(V_{GS}-V_t{)}^2$$

如果将该点在图中画出，即为下图Q点，我们将Q点称为 DC静态工作点 ：

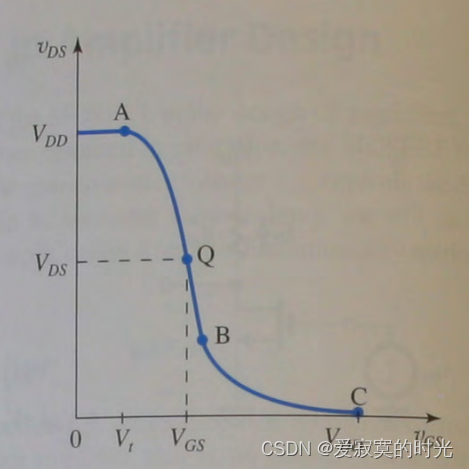
之后，我们在DC的基础上，上叠一个交流时间信号，即 $v_{gs}$ 信号是一个关于时间 $t$ 的函数，那么瞬时值 $v_{GS}$ 为：

$$v_{GS}(t)=V_{GS}+v_{gs}(t)$$

那么总信号源如下：

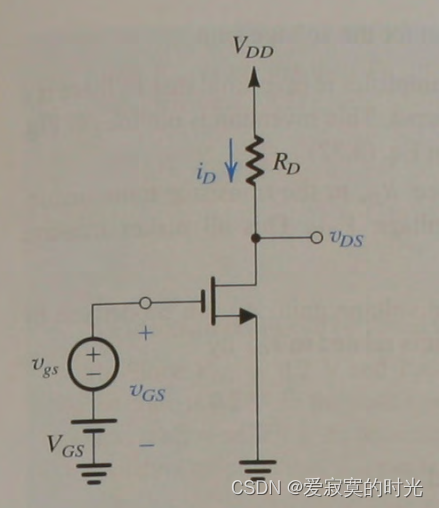
我们假设 $v_{gs}$ 足够小，例如下图的一个足够小的三角波，那么瞬时值点将在 Q 点附近来回摆动：

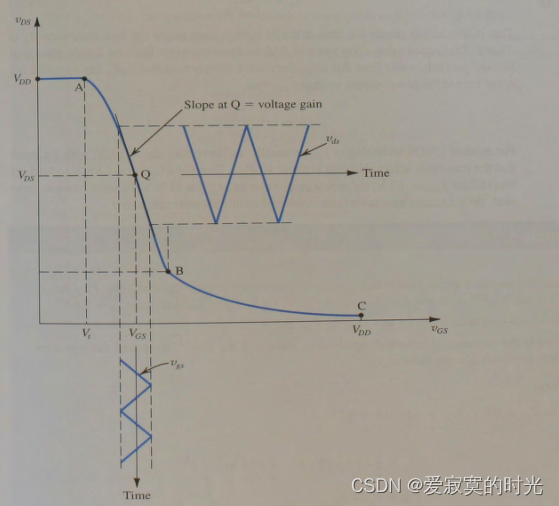
此时 $v_{gs}$ 越小，那么瞬时值点将在 Q 点附近来回摆动幅度就越小，那么Q点附近就越接近于一条直线，就可以实现线性放大。

小信号的电压增益

我们假设 $v_{gs}$ 足够小，那么此时 Q 点处的斜率即为电压增益：

$$A_v\equiv \frac{\partial v_{DS}}{\partial v_{GS}}{|}_{v_{GS}=V_{GS}}$$

求导可得：

$$A_v=-k_n(V_{GS}-V_t)R_D=-k_n{V}_{OV}{R}_D$$

关于电压增益，我们得到以下两点信息：

1. 电压增益为负值，说明输入电压和输出电压的相位差了180度。
2. 电压增益正比于$k_n{V}_{OV}{R}_D$ 。

另外，我们带入 $I_D=\frac{1}{2}{k}_n{V}_{OV}^2$ 得到：

$$A_v=-\frac{I_D{R}_D}{V_{OV}/2}$$

这个式子可以帮我我们计算 $A_v$ 的理论最大值，因为 $R_D$ 的压降的最大值是 $I_D{R}_D=V_{DD}$ （图中B点）。

$$|A_{vmax}|=\frac{V_{DD}}{V_{OV}/2}$$

图像法分析 VTC

尽管我们有上式的电压传导方程，有时我们实际中我们可以通过图像法决定Q点坐标，将MOS管的伏安曲线和电阻的负载曲线取交点。

电阻的负载曲线方程为 $i_D=\frac{V_{DD}}{R_D}-\frac{1}{R_D}{v}_{DS}$ 。

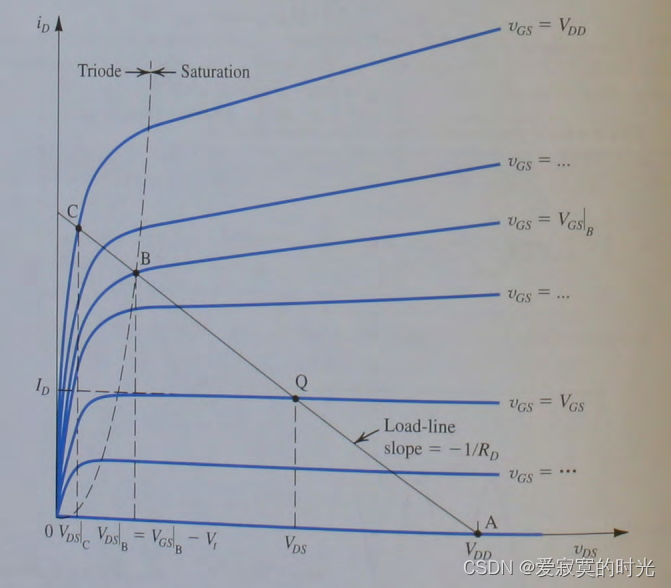
C点代表MOS管工作在深度三极管区，此时三极管表现出一个阻值极小的电阻，同时电压降极小。A点代表MOS管工作在截止区，此时MOS管表现出阻值无限大的开路，如果想让MOS管作为电子开关工作，那么MOS管工作在A和C点之间切换。如下图：

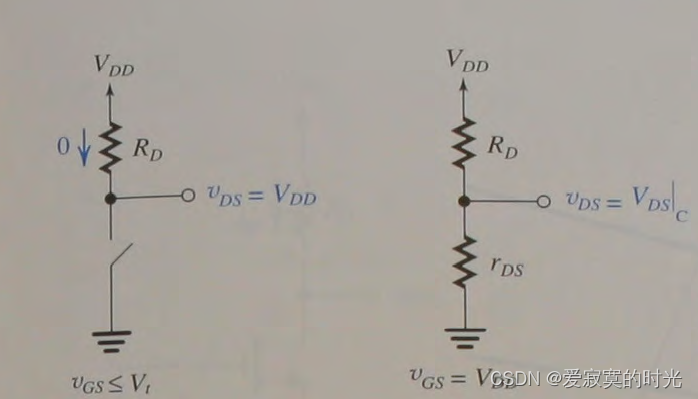
此时 $r_{DS}$ 也称为闭合阻抗。

另外，当MOS管作为放大器使用时，应将Q点偏置在 AC两点之间。

Q点的位置

DC静态点Q点的位置由栅极电压降 $V_{GS}$ 和电阻 $R_D$ 决定，考虑确定一个合理Q点的位置需要考虑两方面因素：

1. 需要的电压增益
2. 信号的最大幅值

当我们固定 $R_D$ 的阻值之后，此时Q点仅由 $V_{GS}$ 决定，我们发现，随着 $V_{GS}$ 增大，电压增益的绝对值就会增大，我们会获得更大的电压增益，但是我们发现信号的最大允许幅值就会减小（因为Q点越接近B点）。这是我们经常需要做出两者之间的权衡。

现在我们来决定 $R_D$ 的值，我们使用图像法来说明这一点：

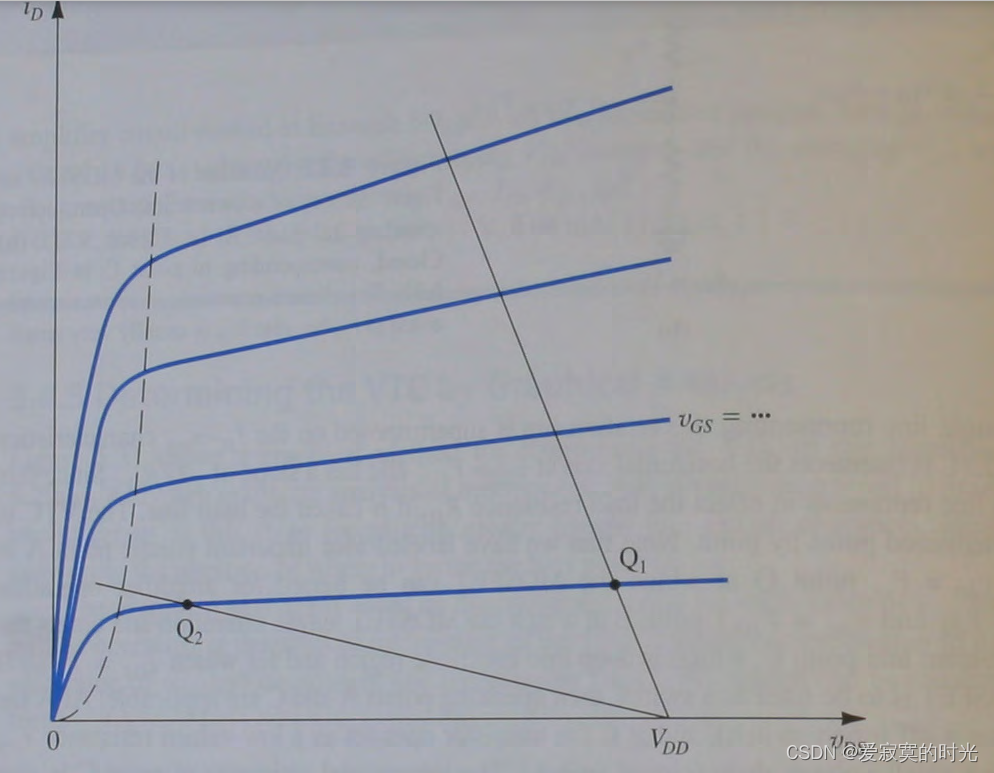
当增大 $R_D$ 固然会得到一个更大的电压增益，但是这将令负载曲线的斜率越小，即 $Q_2$ 点越有可能接近于三极管区，这将减小信号的正向幅值最大值，我们说这个电路没有预留足够的头部空间。同样的，当 $R_D$ 减小，这将减小信号的负向幅值最大值，我们说这个电路没有预留足够的尾部空间。