异或运算在面试题中的应用

news2025/4/22 3:41:01

异或运算是涉及到数据位运算时常见的处理方式。如何进行异或运算？在对应位上，相同为0，不同1，但其实两个数据异或运算就是进行无进位加法。

例如： int a = 7, b = 6, a ^b = ?

算法1: 相同为0，不同为1

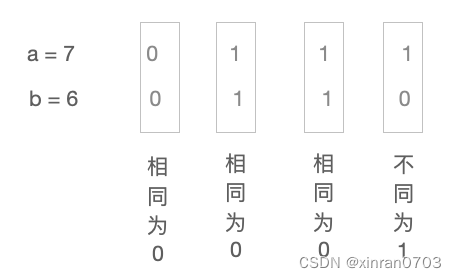
a ^ b= : 0 0 0 1

算法2: 无进位相加

a ^ b= : 0 0 0 1

异或运算的性质

1）0^N == N

2) N^N == 0

3) 异或运算满足交换律和结合律

交换律： a^b = b^a

结合律：a^b^c = a^(b^c)

题目1:如何不用额外变量交换两个数？

//代码段1

#include <stdio.h>

void swap(int* a, int i, int j){
    a[i] = a[i]^a[j];
    a[j] = a[i]^a[j];
    a[i] = a[i]^a[j];
}

int main(){
    
    return 0;
}

代码解析：

为什么执行了 a = a^b; b = a^b; a= a^ b; 这三句代码，a和b的值就被交换了？

设：变量 a = A， b = B；

a = a ^ b; $\Rightarrow$ a = A^B, b = B;

b = a ^ b; $\Rightarrow$ b = B^A^B, 由于异或运算满足交换律，所以，b = B^B^A , 又因为N^N == 0 且 0^N = N, 所以，b = A；

a = a ^ b; $\Rightarrow$ a = A^B^A = B

Tip:

如果使用异或运算交换数据 a 和 b的值， a 和 b的值可以相等，但是二者必须指向不同的内存空间，不能是同一个变量。例如在代码段1中，交换数组a[i] 和a[j] 的值 , a[i] 可以等于 a[j] （a[i] == a[j] == X），但是 i 不可以等于j，因为，如果 i== j ， a[i] ^ a[j] $\Rightarrow$ a[i] ^ a[i] , 根据异或运算的性质，一个数与其自身进行异或运算，结果为0（N^N=== 0). 所以如果 i 等于 j ，执行了swap函数后，a[i] 和 a[j] 都将被置0.

题目2：一个数组中有一种数出现了奇数次，其他数都出现了偶数次，找到并打印这种出现了奇数次的数。

题目解析：

这道题同样是异或运算的性质的应用：N^N == 0 和 0^N == N

两个N异或等于0，那么n个N异或呢？即 N^N^N...^N = ? 结果显而易见，如果n为偶数，那么结果就是0，如果是n为奇数，那么这个连续异或的式子就最终简化为 0 ^N , 继续利用异或的性质，这个结果为N。

综上分析，如果把这个数组中的数据依次执行异或运算, 假设数组名为a，那么

a[0]^ a[1] ^ a[2] ^ ... a[n] 最终结果就是 0 ^ a[i] , a[i] 即为出现了奇数次的那个元素。

代码实现：

//代码段2

#include <stdio.h>

int findOdd(int* a , int n){
    int eor = 0;
    for(int i = 0;i < n;i++){
        eor ^= a[i];
    }
    return eor;
}
int mian(){

    int a[11] = {1,1,1,1,2,2,3,3,3,3,3};
    printf("odd is %d\n",findOdd(a,11));
    return 0;
}

运行结果：

题目3:如何把一个int类型的数，提取出最右侧的1？

题目解析：

题目要求将一个int类型的数的最右侧的1提取出来，那么必然涉及将int型数的二进制表达及相关位运算。例如：int a = 0110 1110 0100 0000, 根据题目要求，要找到它最右侧的1，那么得到的结果应该是 ans = 0000 0000 0100 0000 ，对其它数位的情况并不关心。

如何通过 a 得到结果ans 呢？即 $a \to ans$ 需要经过怎样的运算？ ans = a & (~a +1)

因为ans 要求除了a的最右侧的1保留，其它位上都为0，而一个数与它的相反数做“与”操作，结果就是0，但是最右侧的1被保留，就说明除了最右侧1这一位，其它位都是与其相反数做了“与”操作，因此 (～a+1)就是使a的最右侧1这一位在与反后，又被置成了1.

a = 0110 1110 0100 0000

~a = 1001 0001 1011 1111

~a+1 = 1001 0001 1100 0000

a & (~a+1) = 0000 0000 0100 0000

代码实现：

//代码段3
#include <stdio.h>

int findRight_1(int a){
    return a & (~a+1)
}

另：（～a+1 ）其实就是-a ，代码段3可以写成代码段4，结果是一样的。

//代码段4
#include <stdio.h>

int findRight_1(int a){
    return a & (-a)
}

题目4: 一个数组中有两种数出现了奇数次，其他数都出现了偶数次，怎么找到并打印这两种数？

题目解析：

经过题目2的分析，我们知道如果将这个数组从头到尾的异或一遍，出现了偶数次的数被销掉了，结果为 eor = a ^ b , a 和 b是出现了奇数次的两种数，因为题目明确说了出现奇数次的是两种数，那么 a 不等于 b，所以 eor就不等于0。从左往右依次查看eor每一个bit位，肯定有一个bit位是1，假设是第i位，进一步假设a 的第i位是1， b的第 i 位是 0 。那么，原数组就可以分成两类，第一类为第i位是1的数，第二类为第i位是0的数。

第一类：数组中第 i 位是 1的数	第二类：数组中第 i 位是 0 的数
a	b
出现了偶数次且第 i 位是 1的数	出现了偶数次且第 i 位是 0的数

如果将第一类中的数，从头到尾执行一遍异或运算，会发生什么？"出现了偶数次且第i位为1的数” 依然化为零被销掉了，结果是 ${eor}'$ = a

同理，将第二类中的数，从头到尾执行一遍异或运算，“出现了偶数次且第 i 位为0 的数” 被销掉，结果 ${eor}''$ = b. 但是，在求b时可以利用eor的结果： ${eor}''$ = eor ^ ${eor}'$

难点：

1. 将数组从头到尾执行一遍异或运算，结果为 eor

1. 找到eor 结果中最右端第一个1 的bit 位：bit_i . (这个问题就可以利用题目3 的思路)

2. 遍历数组，找到bit_i 位上都为1 的数据，并保存到数组B；

3 将数组B 从头到尾执行一遍异或运算，结果 ${eor}'$ 就是其中一个奇数次数；

4 ${eor}''$ = ${eor}'$ ^ eor , 得到另一个奇数次数

代码实现

#include <stdio.h>

/* arr :  待处理数组
   n：arr长度
   a：出现奇数次的数据1
   b：出现奇数次的数据2
*/
void findOdd_2(int* arr, int n, int* a, int* b){
    int eor = 0;
    for(int i = 0;i < n;i++){
        eor ^= arr[i];
    }
  
    int bit_1 = eor & (-eor); //提取最右侧的1
 
    int eor_a = 0;
 
    for(int i = 0;i < n;i++){
       if(arr[i] & bit_1){
           eor_a ^= arr[i];
       }
    }

    *a = eor_a;
    *b = eor_a ^ eor;
}
 
int main(){
    int arr[16] = {12,12,12,19,19,19,13,13,13,13,45,45,66,66,66,66};
    int a = 0, b = 0;
    findOdd_2(arr,16,&a,&b);
    printf("a = %d, b = %d\n",a,b);
    return 0;
 }

运行结果：

题目5: 一个数组中有一种数出现K次，其他数都出现了M次，M>1, K<M, 请找到出现了K次的数，要求额外空间复杂度为O(1) ？

题目解析：

首先利用一个实例来进一步解释题目：假设数组A中共有4种数，a, b ,c ,d, 其中，a 出现了k次，b、c 和d 都出现了M次， M>1, k<M.

题目5与题目4很相似，都是根据元素在数组中出现的次数来确定元素值，但是题目5中并未明确数据出现次数的具体值。一个整型数是32个bit位，定义一个大小为32 的数组 int arr[32] , arr[i] 表示原数组中第i位为1 的数据元素的总和，例如，数组A中：

a的第i位为1，b的第i位为1，c 和 d 的第i位为0，则 arr[i] = 1*K+ 1*M +0+0 = k+M；

a的第i+1 位1，b的第i+1位位1， c 的第i+1位为1， d的第i+1位为0，则 arr[i+1] = K+M+M+0 = k+2M;

以此类推，计算出arr中 0～31 个元素的值。

再逆向思考，如果 arr[i] % M == 0 ，说明数组A中只有出现M次的元素在arr[i] 上是1；arr[i] % M != 0, 说明数组A中出现K次的元素在arr[i] 为1.

代码实现：

#include <stdio.h>

int findK(int* arr, int n, int k, int M){
    int bit32[32] = {0};
    for(int i = 0;i < n;i++){  //遍历数组arr中的每个元素
        for(int j = 0; j < 32;j++){ //遍历arr[i] 的32个bit位
            bit32[j] += (arr[i]>>j) & 1; //如果arr[i]的第j个bit位为1，则bit[j] 加1；
        }
    }
    int ans = 0; //出现k次的数据
    for(int i = 0;i < 32;i++){ //遍历数组bit32
        if(bit32[i] % M){ //如果bit[i]% M 不为0，说明在出现K次的数据在第i个bit位上是1
            ans += 1 << i; //将出现k次数据的第i个bit位置为1
        }  
    }
    return ans; 
}

总结：对异或运算的考察，主要是对其性质的考察，在实际问题中能够灵活的运用其性质。上述题目5虽然没有使用异或运算，但是给我们提供了一种利用位运算解决问题的思路。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1824030.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！